CCS

Channel Coding

Communication through noisy channels is subject to errors. In order to decrease the effect
of errors and achieve reliablecommunication, it is necessary to transmit sequences

that are as different as possible so that the channel noise will not change one sequence
into another. This means some redundancy has to be introduced to increase the reliability
of communication. The introduction of redundancy results in transmission of
extra bits and a reduction of the transmission rate.

Channel coding schemes can be generally divided into two classes, block codes and convolutional codes.

In block coding, binary source output sequences of length k
are mapped into binary channel input sequences of length n; therefore, the rate of the
resulting code is k/n bits per transmission. Such a code is called an (n, k) block code
and consists of 2k codewords of length n, usually denoted by c1, c2 , ... , Czk. Mapping
of the information source outputs into channel inputs is done independently, and the
output of the encoder depends only on the current input sequence of length k and not
on the previous input sequences. In convolutional encoding, source outputs of length
ko are mapped into no channel inputs, but the channel inputs depend not only on the
most recent ko source outputs but also on the last (L - 1) ko inputs of the encoder.

Simple Repetition Code

This means that by employing the channel five times, instead of just once, we can reduce
the error probability from 0.001 to 10-9. Of course, a price has been paid for this
more reliable performance; that price is a reduction in the rate of transmission and an
increase in the complexity of the system. The rate of transmission has been decreased
from one binary message per one use of the channel to one binary message per five usages
of the channel.

From the preceding discussion it seems that if we want to reduce the error probability
to zero, we have to increase n indefinitely and, therefore, reduce the transmission
rate to zero. This, however, is not the case, and Shannon showed that one can achieve
asymptotically reliable communication (i.e., Pe --> 0) by keeping the rate of transmission
below the channel capacity, which in the above case is

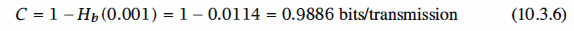
Matlab Coding

% MATLAB script for Illustrative Problem 10.7
echo on
ep=0.3;
for i=1:2:61
    p(i)=0;
    for j=(i+1)/2:i                                                         # (i, j) - the code rate is i / j
                                                                               # binary source output sequences of length j
                                                                               # binary channel input sequences of length i
        p(i)=p(i)+prod(1:i)/(prod(1:j)*prod(1:(i-j)))*ep^j*(1-ep)^(i-j);    # equation 10.3.3
        echo off ;
    end
end
echo on ;

stem((1:2:61),p(1:2:61))
xlabel('n')
ylabel('pe')
title('Error probability as a function of n in simple repetition code')

Reference,

　　1. <<Contemporary Communication System using MATLAB>> - John G. Proakis