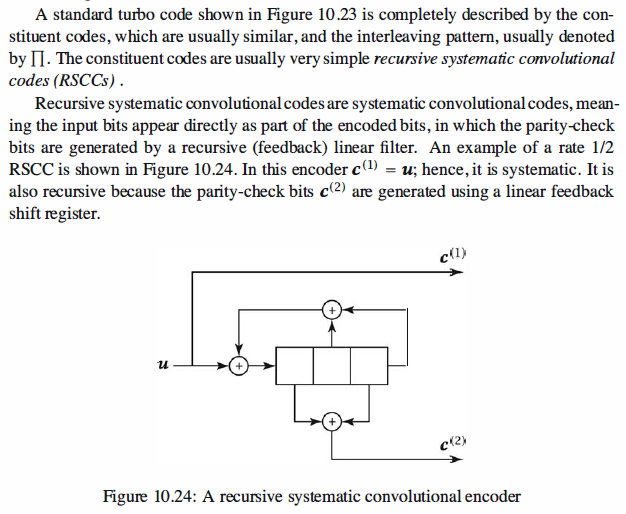
Turbo Codes
Shannon's random coding theorem states that codes achieving channel capacity must
have random, or close to random, distribution as well as large block lengths. However,
in general, for a randomly generated code, the decoding complexity grows exponentially
with the block length of the code. Hence, lack of structure, as well as large
block length, renders maximum likelihood (ML) decoding of capacity achieving codes
impractical. Turbo coding is a method to combine two simple codes connected by
a pseudorandom interleaver of large length to generate a code with close-to-random
structure as well as large block length. However, because the resulting code is based
on combining simple codes, its decoding is possible by an iterative scheme based on
the decoding of its constituent codes. This decoding method, called iterative decoding,
or turbo decoding, is not optimal but for many codes, after a few iterations, has a
performance close to ML decoding.
Parallel concatenated convolutional codes (PCCC) with interleaving, also called
turbo codes, were introduced by Berrou et al. (1993) and Berrou and Glavieux (1996).
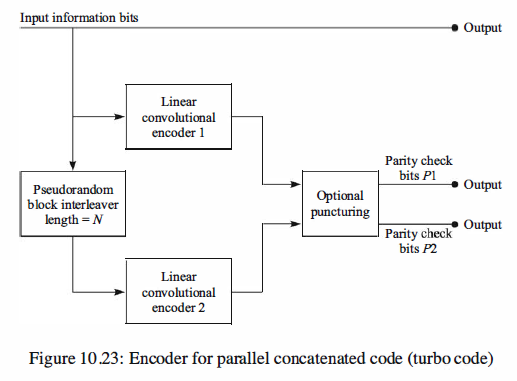
A basic turbo encoder, shown in Figure 10.23, is an encoder that employs two recursive
systematic convolutional encoders in parallel, where the second encoder is preceded by
an interleaver. The two recursive systematic convolutional encoders may be either identical
or different. We observe that the nominal rate at the output of the turbo encoder
is Re = 1/3. However, by puncturing the parity-check bits at the output of the binary
convolutional encoders, we may achieve higher rates, such as rate 1/2 or 2/3.

Matlab Coding

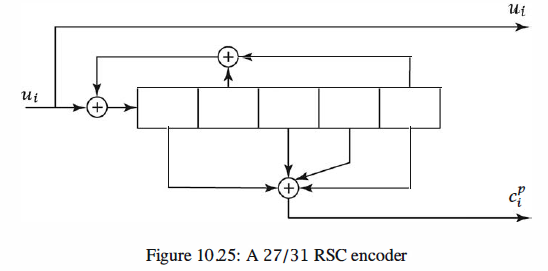
1 function [c_sys,c_pc]=RSCC_57_Encoder(u); 2 % RSCC_57_Encoder Encoder for 5/7 RSCC 3 % [c_sys,c_pc]=RSCC_57_Encoder(u) 4 % returns c_sys the systematic bits and 5 % c_pc, the parity check bits of the code 6 % when input is u and the encoder is 7 % initiated at 0-state. 8 u = [0 1 1 1 0 0 1 0 0 1 1 0 0 1 0 0 1 1 1 1]; 9 L = length(u); 10 l = 1; 11 % Initializing the values of the shift register: 12 r1 = 0; 13 r2 = 0; 14 r3 = 0; 15 while l <= L 16 u_t = u(l); 17 % Generating the systematic bits: 18 c1(l) = u_t; 19 % Updating the values of the shift register: 20 r1_t = mod(mod(r3 + r2,2) + u_t,2); 21 r3 = r2; 22 r2 = r1; 23 r1 = r1_t; 24 % Generating the parity check bits: 25 c2(l) = mod(r1 + r3,2); 26 l = l + 1; 27 end 28 c_cys=c1; 29 c_pc=c2;
>> c_cys
c_cys =
0 1 1 1 0 0 1 0 0 1 1 0 0 1 0 0 1 1 1 1
>> c_pc
c_pc =
0 1 1 1 1 1 1 0 1 0 0 0 1 1 1 1 1 1 0 0
Reference,
1. <<Contemporary Communication System using MATLAB>> - John G. Proakis