排序算法java实现以及简易性能测试

离上一篇博客已经一个星期了，一直想把学到的东西写出来，但总觉得领悟的不够透彻，想写点数据库事务吧，对每种隔离级别所对应的加锁情况以及mvcc只是一知半解；想学着别人写hashmap源码分析吧，看到红黑树，emmmmmmm等我把红黑树弄明白了再好好写一篇hashmap……

那今天，先把八大排序算法实现一遍好了。在之前学数据结构时，八种排序算法大致流程都能弄明白（其实有几个还是有些误解的，捂脸）。

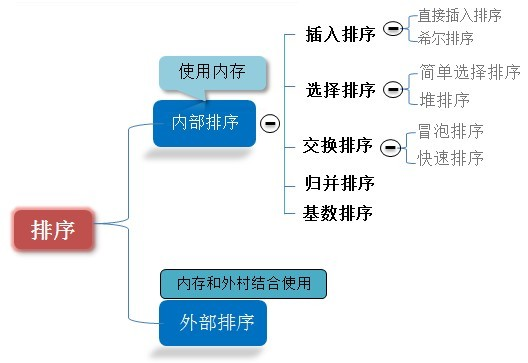
上图的内部排序罗列了八种排序，图是网上找的，那么现在，开始一个个的实现他们吧。（以下内容都是从小到大排序）

1.排序介绍以及实现代码

• 直接插入排序（稳定）

直接插入排序，就是每一轮将第n个元素，插入到前n个已经排序元素中的适当位置，而由于插入的位置是从后往前查找的，因此在排序数组有序时时间复杂度为o(n)。

public static void insertionSort(int[] array) {
    int temp,j;
    for (int i = 0; i < array.length; i++) {
        temp = array[i];
        for (j = i; j > 0 && temp<array[j-1]; j--) {
            array[j] = array[j - 1];
        }
        array[j] = temp;
    }
}

• 希尔排序（不稳定）

希尔排序是插入排序的一种，由于直接插入排序在元素有序时排序效率较高，因此使用增量d对数组进行插入排序处理，使数组尽可能的有序，不断的减小增量至1，当d为1时也就是直接插入排序，不过此时数组已经基本有序，因此排序效率较高。看代码会更直观的感受到希尔排序与直接插入排序的关系。

public static void shellSort(int[] array) {
    int temp,j;
    for (int d = array.length / 2; d >= 1; d /= 2) {//增量不断减小，当d=1时，和直接插入排序一致
        for (int i = 0; i < array.length; i++) {
            temp = array[i];
            for (j = i; j >= d && temp<array[j-d]; j -= d) {
                array[j] = array[j - d];
            }
            array[j] = temp;
        }
    }
}

个人觉得希尔排序耗时与增量d的选取都是一种玄学。

• 简单选择排序（稳定）

简单选择排序就是每次选取一个最小的元素，将其与哨兵位交换。

public static void selectionSort(int[] array) {
    int temp, swap;
    for (int i = 0; i < array.length; i++) {
        temp = i;
        for (int j = i; j < array.length; j++) {
            if (array[i] < array[temp]) {
                temp = i;
            }
        }
        //交换哨兵位以及最小元素的位置，之后的代码都将用swap(array,i,j)表示
        swap = array[i];
        array[i] = array[temp];
        array[temp] = swap;
    }
}

• 堆排序（不稳定）

堆排序，对于基本概念我都理解了，所以，有需要的可以看一下别人的博客，主要流程大概是

1. 初始化建堆，从最后一个有叶子节点的节点开始进行下沉操作，沉完换“前”一个节点下沉，直到根节点下沉完毕。
2. 交换根节点和堆尾节点
3. 对根节点进行下沉操作，此时的下沉的范围比上一次小1

　　然后不断的循环2.3操作，直到下沉范围为1。

/**
 * 堆排序每次都建堆（on^2）
 * 
 * @param array
 */
public static void heapSortWrong(int[] array) {
    int swap;
    for(int i = 0;i<array.length;i++){
        heaplify(array, array.length - i-1);
        
        swap = array[0];
        array[0] = array[array.length - i-1];
        array[array.length - i-1] = swap;
    }
}

/**
 * 建堆过程
 * @param array
 * @param size
 */
public static void heaplify(int[] array,int size){
    for(int i = (size-1)/2;i>=0;i--){//从最后一个子节点的父节点开始下沉
        siftDown(array, size, i);
    }
}

/**
 * 对第parent个元素进行下沉调整
 * @param array
 * @param size
 * @param parent
 */
public static void siftDown(int[] array,int size,int parent) {
    int swap,big;
    while(size >= (parent*2)+1){//如果存在左子节点
        big = (parent*2)+1;
        if((parent*2)+2<=size && array[big] < array[big+1]){//存在右子节点，且右节点比左节点大
            big++;
        }
        if(array[big] >array[parent]){
            swap = array[big];
            array[big] = array[parent];
            array[parent] = swap;
            
            parent = big;
        }else {
            break;
        }
    }
}

一开始对于第3步操作也进行了同1的建堆操作，于是跑出来的“堆排序”和冒泡差不多快。当然也可以用PriorityQueue模拟堆排序

/**
 * 用PriorityQueue模拟堆排序
 * @param array
 */
public static void heapSortPriority(int[] array) {
    PriorityQueue<Integer> queue = new PriorityQueue<>();
    for(int i = 0;i<array.length;i++){
        queue.add(array[i]);
    }
    for(int i = 0;i<array.length;i++){
        array[i] = queue.poll();
    }
}

对于topK问题，维护一个大小为K的小顶堆可以解决，不论数据是否可以一次性放入内存，都可以用小顶堆解决。当然你要是故意为难我说k大到k个元素无法一次性放入内存，那我……我，就有点为难了，不过内外存结合的归并排序应该可以解决。

• 冒泡排序（稳定）

不多说，上代码

public static void bubbleSort(int[] array) {
    int swap;
    for (int i = 0; i < array.length; i++) {
        for (int j = 0; j < array.length - i - 1; j++) {
            if (array[j] > array[j + 1]) {
                swap = array[j];
                array[j] = array[j + 1];
                array[j + 1] = swap;
            }
        }
    }
}

• 快速排序（不稳定）

emmm，不知道说什么，快排写了好几次了，今天又死循环了，于是我给了自己一个嘴巴子，默默的加上了两个‘=’。（再忘记我就，我就再也不手写快排了）。

public static void quickSort(int[] array) {
    qSort(array, 0, array.length - 1);
}

public static void qSort(int[] array, int l, int r) {
    if (l < r) {
        int ll = l;
        int rr = r;
        int x = array[ll];
        while (ll < rr) {
            while (array[rr] >= x && ll < rr)//嘴巴子
                rr--;
            array[ll] = array[rr];
            while (array[ll] <= x && ll < rr)
                ll++;
            array[rr] = array[ll];
        }
        array[ll] = x;
        qSort(array, l, ll-1);
        qSort(array, ll+1, rr);
    }
}

有序时间复杂度o（n^2），无序接近o(nlogn)。

• 归并排序（稳定）

之前没写过归并，不过就是“归”与“合并”两个过程。

public static void mergeSort(int[] array) {
    copy = new int[array.length];
    mSort(array, 0, array.length-1);
}

public static void mSort(int[] array,int l,int r){
    if(l<r){
        int mid = (l+r)/2;
        mSort(array, l, mid);
        mSort(array, mid+1, r);
        merge(array, l, mid, r);
    }
}
static int[] copy;
public static void merge(int[] array,int l,int mid,int r){//合并
    int i = l,j = mid+1;
    for(int k = l;k<=r;k++){
        copy[k] = array[k];
    }
    
    for(int k = l; k<=r;k++){
        if(i>mid){
            array[k] = copy[j++];
        }else if (j>r) {
            array[k] = copy[i++];
        }else if (copy[i] <= copy[j]) {
            array[k] = copy[i++];
        }else {
            array[k] = copy[j++];
        }
    }
}

稳定的排序，时间复杂度也是稳定的o(nlogn)。

• 基数排序

基数排序其实就是多次桶排序，而桶排序对数据范围有一定的要求，不然桶空间就会过大，而基数排序虽然进行多次桶排序，对数据的范围要求有一定的降低，但是当数据分布过大时，如何设置桶的范围对排序性能有较大的影响，说了这么多，其实就是想说我没写基数排序，嘻嘻，因为基数排序比较适合特定的场景，比如说对日期-时间进行排序。

2.运行结果

对于有序数据，插入排序的性能确实较高，但是对于大量无序数据，快排的性能较为优异，归并以及（玄学）希尔排序的性能也不差。

下图是500个正序数据，500个随机数据，以及5000个随即数据所使用的时间。基本符合理论时间复杂度。

500正序：

500随即：

5000随即：

使用自己写的堆排序以及PriorityQueue的耗时变化主要在于元素少时，jdk实现的PriorityQueue内部使用的移位比我的乘除耗时少一些，而元素多时，把元素从数组复制到PriorityQueue再移到数组中耗时较大。

测试以及排序源码：点我。

那么，收工，睡觉！