傅里叶变换、卷积、数字滤波
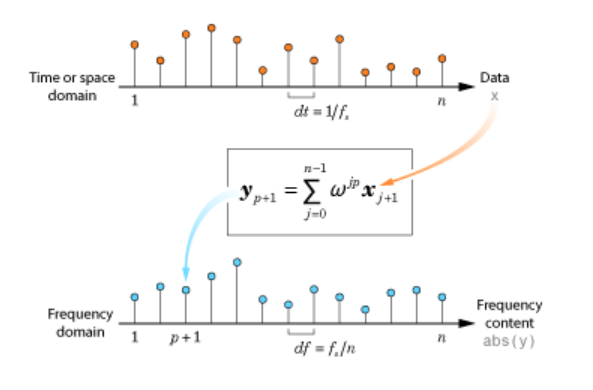
变换和滤波器是用于处理和分析离散数据的工具,常用在信号处理应用和计算数学中。当数据表示为时间或空间的函数时,傅里叶变换会将数据分解为频率分量。fft 函数使用快速傅里叶变换算法,相对于其他直接实现,这种方式能够减少计算成本。有关傅里叶分析的更多详细介绍,请参阅傅里叶变换。在使用传递函数修改输入数据的幅值或相位时,conv 和 filter 函数也是很有用的工具。
函数:
fft |
快速傅里叶变换 |
fft2 |
二维快速傅里叶变换 |
fftn |
N 维快速傅里叶变换 |
nufft |
非均匀快速傅里叶变换 |
nufftn |
N 维非均匀快速傅里叶变换 |
fftshift |
将零频分量移到频谱中心 |
fftw |
定义用来确定 FFT 算法的方法 |
ifft |
快速傅里叶逆变换 |
ifft2 |
二维快速傅里叶逆变换 |
ifftn |
多维快速傅里叶逆变换 |
ifftshift |
逆零频平移 |
nextpow2 |
2 的更高次幂的指数 |
interpft |
一维插值(FFT 方法) |
卷积:
conv |
卷积和多项式乘法 |
conv2 |
二维卷积 |
convn |
N 维卷积 |
deconv |
去卷积和多项式除法 |
数字滤波:
filter |
1 维数字滤波器 |
filter2 |
二维数字滤波器 |
ss2tf |
将状态空间表示形式转换为传递函数 |
padecoef |
时滞的 Padé 逼近 |
主题
傅里叶变换是用于在许多应用中分析数据的强大工具,包括用于信号处理的傅里叶分析。
使用傅里叶变换对时域信号进行频率和功率谱分析。
将二维光学数据变换为频率空间。
使用卷积对含噪二维数据进行平滑处理。
滤波是一种数据处理技术,用于使数据平滑或修改特定数据特性(例如信号振幅)。
https://ww2.mathworks.cn/help/matlab/fourier-analysis-and-filtering.html?s_tid=srchbrcm