梯度下降法
- 不是一个机器学习算法
- 是一种基于搜索的最优化方法
- 作用：最小化一个损失函数
- 梯度上升法：最大化一个效用函数
举个栗子
直线方程：导数代表斜率
曲线方程：导数代表切线斜率
导数可以代表方向，对应J增大的方向。对于蓝点，斜率为负，西塔减少时J增加，西塔增加时J减少，我们想让J减小，对应导数的负方向，因此前面需要加上负号。
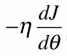（伊塔对应步长）-------（1）
用当前点的西塔加上（1）式，得到新的西塔。因为导数是负值，前面又有负号，所以整个是正值，加上一个正值对应西塔在增大。
多维函数中，对各维求导数，其实就是梯度。
当点取在右边时，（1）式也成立。此时斜率为正，西塔增加J增加，西塔减少J减少，我们想让J减少因此我们前面也要加上负号。此时相当于 西塔减去一个正值 -> 西塔变小了 -> 在向着左边移动。
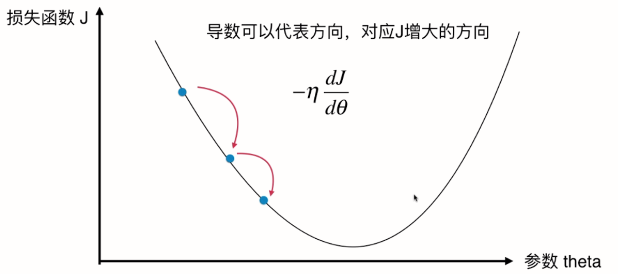
我们可以想成这是一个山谷，放一个球下来，球自然会滚到最低处。梯度下降即在模拟这个过程。球滚落的速率 即由 伊塔 决定。
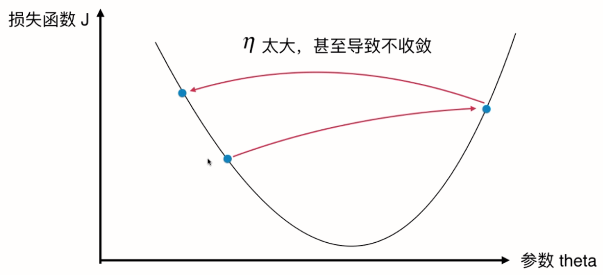
并不是所有函数都有唯一的极值点
如果从最右侧的点开始搜索，找到局部最优解后就结束了。
注：对于线性回归来说，
多元线性回归中的梯度下降法
n代表有n个维度的特征值，即求，
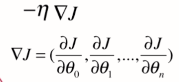，梯度
这个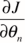
是偏导数的意思。偏导数与导数（d）求法一致，只是J中包含多个西塔（未知量），现在只对其中一个西塔求导数则称为偏导数。
因此
举个栗子，二维特征（x，y）梯度下降法可视化，z对应损失函数的取值：
梯度方向对应下降最快的那个方向。
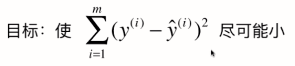，这个式子即J
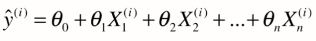
代入上式，即
求导时 西塔 是未知数，x，y都是在监督样本中获取的已知信息
我们会发现这个公式每一项中是一个m项的求和，梯度大小即与样本数量相关，样本数量越大，我们得到的梯度中每一个元素也越大，但这明显不合理。我们希望与m无关，因此我们让整个梯度值除以m。
因此，目标函数可改成，
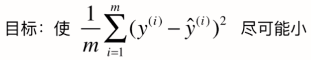
我们可发现这个式子即MSE的值，
-----（一般我们用这种）
，为了将求导得到2的系数约掉。
其中，
梯度下降法的向量化
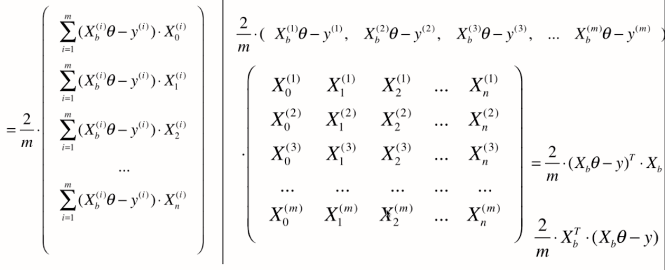
因此，
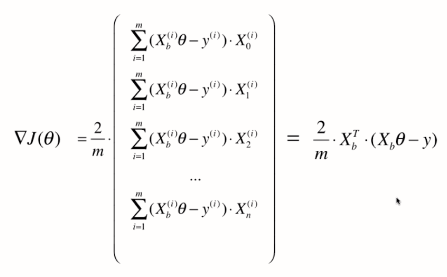
我们之前说的梯度下降法都是将我们想要最优化的损失函数相应在某一点的西塔的梯度值准确的求出来。
通过上面推导的这个公式，可以看出要想求出准确的梯度来，在公式中每一项都要对所有样本进行计算（前面有西格玛m）。
这种梯度下降法又称为 批量梯度下降法Batch Gradient Descent
每一次计算的过程都要将样本中的所有信息批量的进行计算，但显然当样本量m非常大时，计算梯度本身也是十分耗时的。
========>改进方案
由于每一项都对m个样本进行了计算，最后我们为了取平均还除以了m。所以我们可以每次只对其中的一个样本进行计算？
西格玛去掉， 对于 i 每次都随机取固定的一个 i ， 相应大括号外也不需要除以m，直接乘以2就好了。
此时对于大Xb来说，每次我们只取一行来进行计算。
我们使用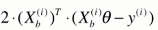
这个式子来作为我们搜索的方向。（注：是搜索的方向不是梯度的方向，因为此时这个式子已经不是我们损失函数的梯度了）
每次随机取一个维度特征的导数的方向来作为前进搜索的方向，不断迭代。
折种思想称为 随机梯度下降法Stochastic Gradient Descent
随机梯度的方法对比批量梯度下降法，批量梯度下降法是：从外面的一点开始搜索，将会坚定不移的朝着一个固定的方向，也就是整个损失函数最小值的方向向前移动。
但随机梯度它不能保证每一次得到的方向一定是损失函数减小的方向，更不能保证是减小最快的方向，所以搜索路径会如上图所示。这也是随机的特点，具有一定的不可预知性。
但即使如此，我们通过随机梯度下降法也能差不多来到整个函数相应最小值的附近。虽然不像批量梯度下降法一样一定来到最小值固定的位置。但当m比较大时，我们愿意用一定的精度来换取一定的时间。这也是随机梯度下降法的意义。
而且在具体实现中，重要技巧：随机梯度下降法中 学习率的取值变得非常重要。
因为假如学习率eta一直取一个固定值，很可能随机梯度下降法已经来到最小值附近，但由于随机过程不够好，eta又是固定值，慢慢又跳出了最小值范围。因此我们希望学习率是逐渐递减的，设计一个函数，使eta随着梯度下降法循环次数的增加而递减，如，
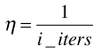
但这种实现的问题是：当循环次数比较少时，eta下降太快。当循环次数从1变到2，我们eta一下子下降了50%，但从10000到10001，eta只下降了万分之一。前后eta值下降比率差别太大。
通常具体实现时，我们在分母添加一个常数b来缓解这种情况，即
，b通常取50
对于分子如果固定取1有时候也达不到理想的效果，因此分子也取一个常数a，比1灵活一些，即
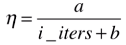，a通常取5
a和b，即随机梯度下降法对应的两个超参数。
在随机梯度下降法中，为了得到较好的收敛效果，学习率随循环次数增加而递减。这种思想是模拟在搜索领域中的模拟退火思想。打造钢铁用火炼，火炼的温度从高逐渐到低逐渐冷却，即所谓退火的过程。冷却的函数与时间t相关。因此有时也将a，b用t0，t1表示。
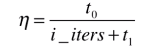
关于梯度的调试
求出定义的损失函数在某点西塔上对应的梯度是什么。
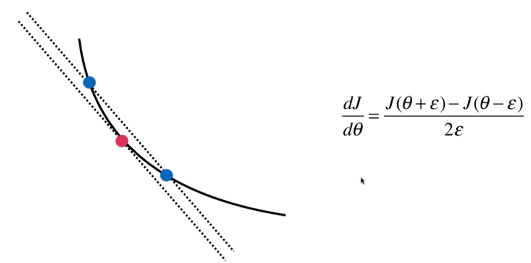
例如要求曲线上红点的梯度，即红点的导数，即在该点切线的斜率。
我们可使用一种方式来模拟这跟切线的斜率，在红点左右两边各取一点(西塔+伊普习隆，西塔-伊普习隆)，蓝色两点连线的斜率应近似于红点的斜率。（当伊普习隆无限小时，对应红点切线斜率的定义）
红点斜率 约等于 蓝色两点连线的斜率 = 纵坐标差 / 横坐标差
推广到多维，也同样适用，
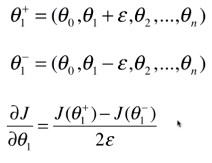
以此类推，我们可以用这种方式求出每个维度对应的导数，合起来即大J在西塔上的梯度。
这种做法比之前用数学公式推导求法，从数学角度来说更直观易懂，但时间复杂度是非常高的。因为每求一个维度对应的导数，我们需要求两遍（左，右）把西塔值代入大J。如果大J复杂度非常高，那么我们每求一次梯度都将消耗非常多的时间。
所以这种方法是作为调试的手段。在还没完成我们的算法时，先在小数据量用这种方法来得到最终的结果。我们知道这个结果肯定是对的。然后我们再用推导公式的方法来看最终求得的梯度与使用这种方法求得的梯度是否能对上。
总结
- 批量梯度下降法Batch Gradient Descent
- 随机梯度下降法Stochastic Gradient Descent
- 小批量梯度下降法Mini-Batch Gradient Descent
批量梯度下降法每次求一个点的梯度要把所有样本都看一遍，随机梯度只用看一个样本。但批量法就比较慢，优点是稳定，一定向着最小化的方向前进。随机的优点是快一些，但缺点是随机，不一定朝着最小的方向前进。而小批量梯度下降法则结合了两者的优缺点，每次不止看一个样本，看k个样本。更具有代表性，也更快。
随机===>运算速度更快，跳出局部最优解，更具整体全局观
机器学习领域很多算法都使用随机的特点，如 随机搜索，随机森林。因为解决的问题很多都是在不确定的世界中求解不确定的解。