codeforces#323(div2) C. GCD Table 贪心
The GCD table G of size n × n for an array of positive integers a of length n is defined by formula
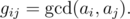
Let us remind you that the greatest common divisor (GCD) of two positive integers x and y is the greatest integer that is divisor of both xand y, it is denoted as 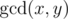 . For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:
. For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:
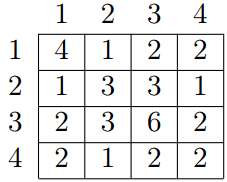
Given all the numbers of the GCD table G, restore array a.
The first line contains number n (1 ≤ n ≤ 500) — the length of array a. The second line contains n2 space-separated numbers — the elements of the GCD table of G for array a.
All the numbers in the table are positive integers, not exceeding 109. Note that the elements are given in an arbitrary order. It is guaranteed that the set of the input data corresponds to some array a.
In the single line print n positive integers — the elements of array a. If there are multiple possible solutions, you are allowed to print any of them.
4
2 1 2 3 4 3 2 6 1 1 2 2 1 2 3 2
4 3 6 2
1
42
42
2
1 1 1 1
1 1
先统计次数再从大到小删除就行了,每个数会和添加进的数贡献出两个gcd。


#include<bits/stdc++.h> #define REP(i,a,b) for(int i=a;i<=b;i++) #define MS0(a) memset(a,0,sizeof(a)) using namespace std; typedef long long ll; const int maxn=1000100; const int INF=(1<<29); int n; ll a[maxn]; map<ll,int> cnt; ll s[maxn],sz; ll b[maxn],m; int main() { while(cin>>n){ cnt.clear();sz=0; REP(i,1,n*n) scanf("%I64d",&a[i]),cnt[a[i]]++,s[++sz]=a[i]; sort(s+1,s+n*n+1); sz=unique(s+1,s+n*n+1)-(s+1); m=0; for(int i=sz;i>=1;i--){ ll t=s[i]; while(cnt[t]){ REP(i,1,m) cnt[__gcd(t,b[i])]-=2; cnt[t]--; b[++m]=t; } } REP(i,1,m){ if(i==m) printf("%I64d ",b[i]); else printf("%I64d ",b[i]); } } return 0; }