该笔记介绍的是《卷积神经网络》系列第四周:特殊应用(1)人脸识别。
主要内容有:
1.人脸验证与人脸识别
2.一次学习
3.siamese网络
4.Triplet损失
5.二分法实现人脸验证
人脸验证与人脸识别
要理解怎么实现人脸识别,首先要区分人脸验证与人脸识别的差别:
人脸验证(1:1问题):
a.输入一张人物图片和某人的名字或者ID。
b.系统验证输入的图片是否和名字对应。
人脸识别(1:n问题):
a.拥有一个数据集K含有n个人的图片。
b.输入一张人物图片
c.如果输入图片的人物包含在数据集K里,输出名字或者ID。
一般的人脸验证算法不能直接应用在人脸识别算法中,因为人脸识别存在数据集K使其成为了1:n的问题,人脸验证算法的误差会被放大n倍,除非其精度特别高比如达到99.9%。
一次学习
一次学习指的是,系统只能通过一个样本进行学习,使其能够认出同一个人。这也是人脸识别的难点所在,也决定着无法通过传统卷积方法进行训练。
传统卷积方法:

存在的缺点:
a.数据集太小,训练集等于你想要识别人物的数量
b.每次新增数据集,需要重新训练网络
学习similarity函数:
引入一个d函数:放入同一个人的两张图片,它能输出很小的值。放入长相差异很大的人的图片,它会输出一个很大的值。
d(img1,img2)=img1与img2的差异程度
差异程度:
if(d(img1,img2)) <= τ print "same"
>= τ print "differet"
*τ为阀值
在作业说过这种算法也不理想,会因为像素由光线变化、人脸方位、甚至头部微小的变化而发生显著的影响。
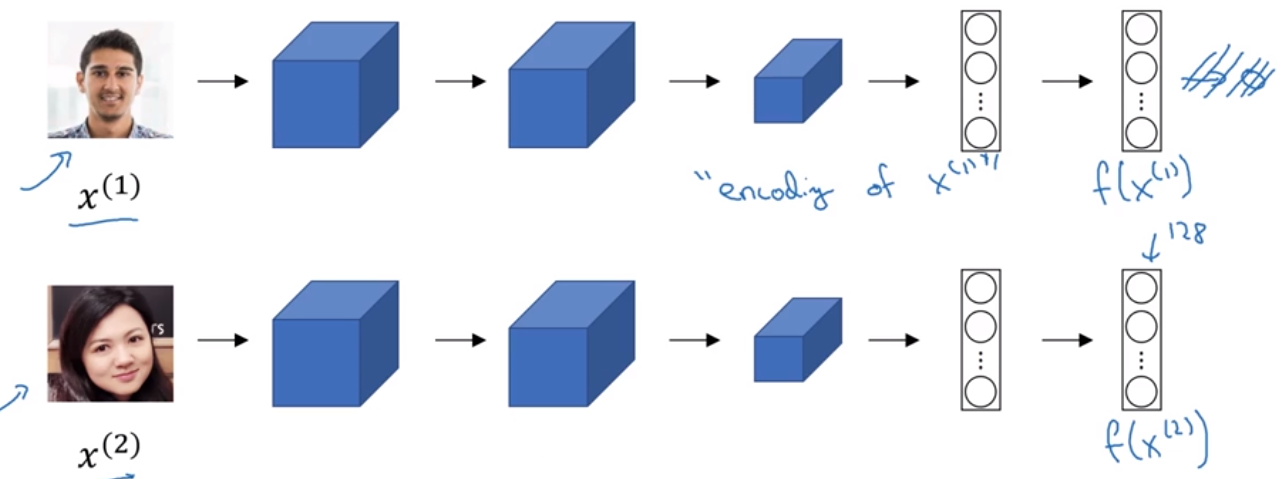
Siamese网络
实现similartity函数,需要使用Siamese网络。Siamese网络是对两个不同的输入,运行相同的卷积神经网络,然后比较它们的差异(全连接层输出的参数)。
神经网络对输出的全连接层定义了一个编码函数f(xi),及similartity函数为:
d(x1,X2)=||f(x1)-f(x2)||
学习参数做的是:
xi,xj是同一个人,则||f(xi)-f(xj)||很小,及编码距离很小
xi,xj不是同一个人,则||f(xi)-f(xj)||很大,及编码距离很大
Triplet损失
Triplet是一个三元组,Triplet的构成是从训练集取出一个样本,称样本为A(anchor),再选一个与A同类的样本P(positive)和与A不同类的样本N(negative)分别组成不同的样本集(A,P)和(A,N),使(A,P)的距离很近,(A,N)的距离更远一点。
三元组定义的损失:
L(A,P,N)=Max(||f(A)-f(P)||2-||f(A)-f(N)||2+α,0)
当L(A,P,N)小于零时,判断损失为0。当||f(A)-f(P)||2-||f(A)-f(N)||2+α大于零时得到一个正的损失值。最终使||f(A)-f(P)||2-||f(A)-f(N)||2小于等于0。
函数推导:
||f(A)-f(P)||2<||f(A)-f(N)||2 //(A,P)的距离很近,(A,N)的距离远
||f(A)-f(P)||2-||f(A)-f(N)||2<0 //简单平移
||f(A)-f(P)||2-||f(A)-f(N)||2<0-α //加入间隔α排除无用输出f(img)=0,间隔α为超参数可手动调试
||f(A)-f(P)||2-||f(A)-f(N)||2+α<0 //简单平移
代价函数:
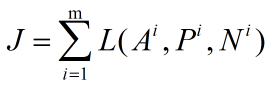
训练集的选择:
a.选择多个人平均n张照片
b.选择更难训练的三人组,主要是对于(A,N)数据集的选择,虽然是不同的人但是相似点要有的,以帮助网络更好的区分。
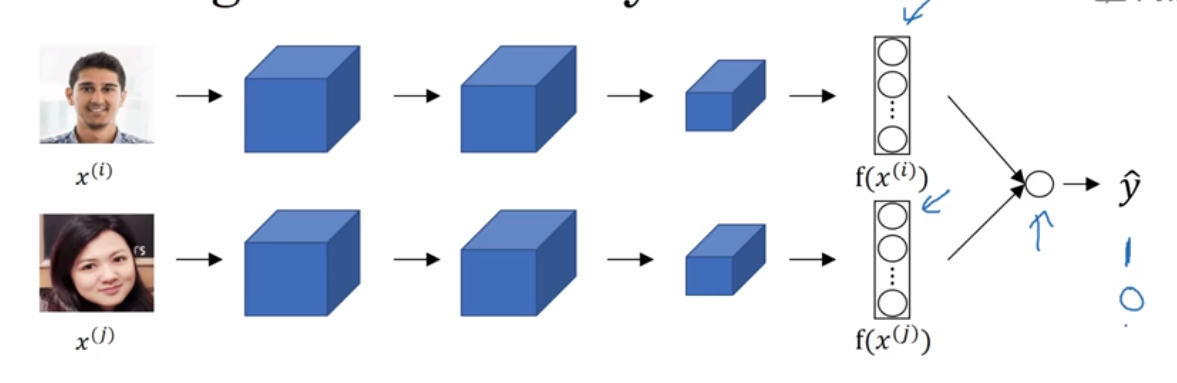
二分法实现人脸验证
把人脸识别当成一个二分法的过程,使用Siamese网络
对于最后逻辑回归单元的处理
元素差的绝对值公式:
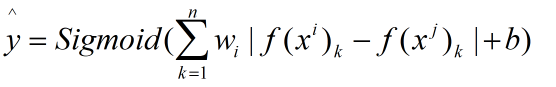
X的平方公式:
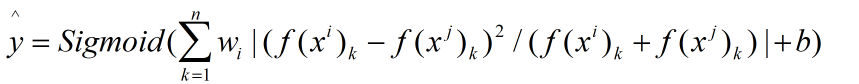
由于使用的是Siamese网络原理也是利用编码不同,判断输入的两张图片是否为同一个人。