Beans (最大不连续子序列和)

Beans

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2637    Accepted Submission(s): 1302

Problem Description

Bean-eating is an interesting game, everyone owns an M*N matrix, which is filled with different qualities beans. Meantime, there is only one bean in any 1*1 grid. Now you want to eat the beans and collect the qualities, but everyone must obey by the following rules: if you eat the bean at the coordinate(x, y), you can’t eat the beans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), and the both rows whose abscissas are x-1 and x+1.


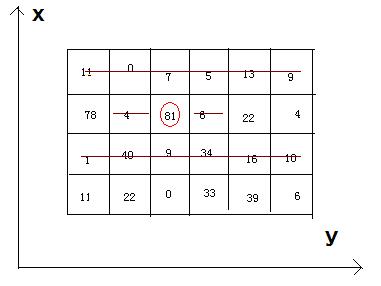
Now, how much qualities can you eat and then get ?

 

Input

There are a few cases. In each case, there are two integer M (row number) and N (column number). The next M lines each contain N integers, representing the qualities of the beans. We can make sure that the quality of bean isn't beyond 1000, and 1<=M*N<=200000.

 

Output

For each case, you just output the MAX qualities you can eat and then get.

 

Sample Input

4 6 11 0 7 5 13 9 78 4 81 6 22 4 1 40 9 34 16 10 11 22 0 33 39 6

 

Sample Output

242

 

Source

2009 Multi-University Training Contest 4 - Host by HDU

 

Recommend

gaojie

 

这道题是说取一个数字，那么相邻的两行的所有数字和同一行的相邻两列的数字就不能再取了。

 

在同一行里面，相邻的数字不能同时取，那么每一行都有会有一个最大值，那么可以把每一行最大值看成一个数字，再求一次，相当于在一行里面求最大不连续子序列的和，只是这里的每一个数字是每一行的最大值。先求出每一行的最大值然后我们再看我们到底应该去取哪一行。

dp[i]=max(dp[i-2]+a[i],dp[i-1])

dp[i]代表到i时的最大子序列的和，对于每一个数字，我只有取或者不取两种状态，如果取，那么我的最大值是从dp[i-2]再加上本身的数值，如果不取，那么我最大值是dp[i-1]。

 

 

感觉这个和01背包很像，取a[i]这个位置和不取a[i]这个位置

 

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define LL long long
using namespace std;
const int MAXN = 200005;

int n,m;
int dp[MAXN];
int a[MAXN];


int main()
{
   // freopen("../in.txt","r",stdin);
    while (~scanf("%d%d",&n,&m))
    {
        memset(a, 0, sizeof(a));
        for (int i=1;i<=n;i++)
        {
            for (int j=1;j<=m;j++)
            {
                scanf("%d",&a[j]);
            }
            for (int j=2;j<=m;j++)
            {
                a[j] = max(a[j-2]+a[j],a[j-1]);
            }
            dp[i] = a[m];
        }
        for (int i=1;i<=n;i++)
        {
            dp[i] = max(dp[i-2]+dp[i],dp[i-1]);
        }
        printf("%d
",dp[n]);
    }
    return 0;
}