定义
马氏距离的定义相关资料太多了,我这里直接截图维基百科上的定义。

特点
马氏距离具有以下特点:
- 马氏距离不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关,即独立于测量尺度。采用数据预处理中的标准化和中心化等方法所获得的马氏距离相同;
- 马氏距离具有放大变化微小的变量的作用,这对于化学指纹图谱的分析而言是有利的特点;
- 马氏距离在计算中考虑了各自变量之间的线性相关关系,因此可以排除变量之间相关性的干扰;
- 马氏距离可用于鉴别离群值。一个马氏距离较大的样本必然是一个离群值;
- 应用马氏距离的前提是各自变量均应符合正态分布。
马氏距离与欧氏距离的主要区别点在于:
- 欧氏距离有量纲,将各自变量的差别同等对待;马氏距离无量纲;
- 欧氏距离不考虑变量间的相关性,马氏距离根据协方差矩阵消除了相关性;
- 如果协方差矩阵为单位矩阵,则马氏距离就简化为欧氏距离;
意义
上面的内容,很多博客也总结过了。其实看完后对马氏距离并没有一个很直观的认识。这里总结一下马氏距离的意义和解释为什么马氏距离比欧式距离更好的检测异常点。这里的内容主要总结自如何理解马氏距离,多维Mahalanobis距离是否要用到“互相关张量”来进行描述?
欧式距离是定义在两个点之间,维度的多少,不会使得欧式距离更复杂。欧氏距离认为多维空间是各向相同的,往哪个方向走,意义都一样。
马氏距离认为各向是异向的。而各向异性的具体参数,由一个协方差矩阵表示。可以把直观协方差矩阵当成一个多维正太分布的协方差阵,那么这个分布的密度函数的等高线,就是等高线常见的椭圆。从椭圆中心到椭圆上各个方向的点的马氏距离,都是相等的。
其中,椭圆的各个轴的方向,是协方差矩阵的特征向量。各个轴的长度正比于协方差矩阵的特征值的平方根。
下面用一个图来说明一下。
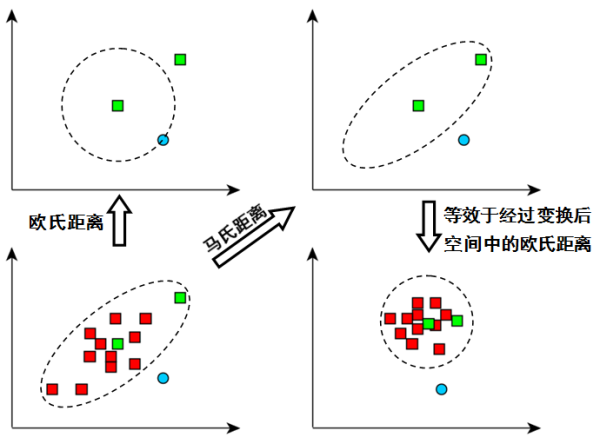
左下角在二维空间中由一个分布产生的方块样本,这个分布的一条等高线如虚线的椭圆框所示,图中还有一个不属于该分布的圆圈样本。这是是一个典型的欧式距离会把分布外样本算的更近的例子,比如把绿色和蓝色样本单拎出来,就是左上角的图,蓝色小圆圈和中心的绿色方块更近了,这是因为单纯的欧式距离无法反应方块的分布。这种情况下,考虑用马氏距离。这里默认方块的分布可以由协方差矩阵很好描述。这样计算出的距离就像说的一样不再是各向同性,对于方块的分布而言有个良好性质是分布的等高线上到中心的马氏距离相等了,因为马氏距离包含了方块本身分布的信息。
进一步来理解,马氏距离可以表示为下面这样:
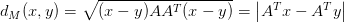
其实等效于做了个线性变换,然后在变换后的空间中求了下欧式距离。