矩阵快速幂 优化dp 模板

 相关博客 ：https://blog.csdn.net/china_xyc/article/details/89819376#commentBox

关于能用矩阵乘法优化的DP题目，有如下几个要求：

1. 转移式只有加法，清零，减法etc.，max和min运算不允许
2. 转移式中关于前几位dp结果得到的系数必须是常量
3. 转移次数一般超级多
4. 由于转移次数多，一般都要模一个int范围内的数

综上，举一个例子：

dp[i]=a×dp[i−1]+b×dp[i−2]+c×dp[i−3]

其中，a,b,c是常量，而在需要矩阵优化的DP中，往往 i 在2^128之类的，特别鬼畜的特别大的数；
因为矩阵乘法优化后求dp[ i ] 是在O log（i）的时间内完成的。
那么，关于矩阵乘法如何实现，它的原理又是啥呢？
矩阵乘法需要两个矩阵A与B，A是n×p，B是p×m的大小，如下图

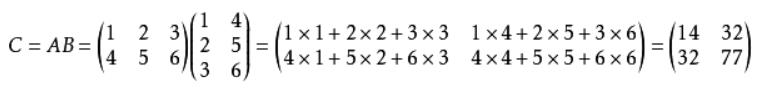
为了方便解释，我们举斐波那契的例子。
斐波那契的转移式是：dp[ i ]=dp[ i-1 ]+dp[ i-2 ]。
那么我们把（dp[ i ]，dp[ i-1 ]）看做一个1×2的矩阵A
而每次转移相当于把A乘以矩阵F：
|1 1|
|1 0|
得出的结果是：（dp[i]+dp[i−1]，dp[i]），也就是（dp[i+1]，dp[i]）
那么每次进行一次矩阵乘法需要8次运算，而原先的状态转移只需要1次，这么看矩阵乘法不就一废柴算法吗。。
关键的是！矩阵乘法具有结合律， 嘿嘿嘿，那么我们就可以开始快速幂了！这样一下吧O（n）的朴素算法优化成了O（8×logn）的算法，在n炒鸡炒鸡变态大的时候我们就可以用这个优化了。

自己做到的例题 https://www.luogu.org/problem/P5343

用到的知识：集合取交集( bitset<N> 和 &=)  线性递推(DP)  矩阵加速(矩阵快速幂)  （其实有点像滚动数组）
线性递推 就是这种感觉： f ( n ) = f ( n-1 ) + f ( n-2 ) , 然后知道 f（1）, f ( 2 )  的值，推出 f ( 3 ) 的值 ，再一直递推下去，是先知道前面的值再去知道后面的值的。

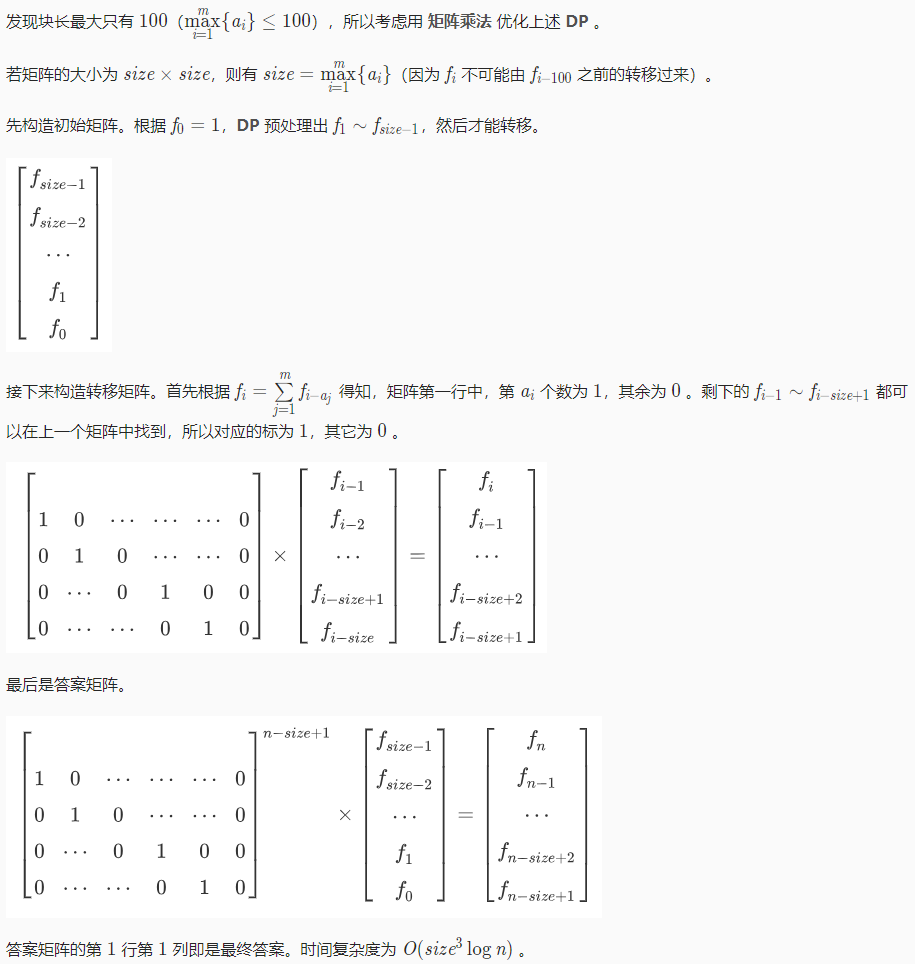
#include <cstdio>
#include <cstring>
#include <iostream>
#include <bitset>
#include <algorithm>
using namespace std;

typedef long long ll;
const int maxn = 105;
const int mod = 1e9+7;
ll n;
int m,x;
bitset<maxn> a,b;
ll g[maxn][maxn],tmp[maxn][maxn],res[maxn][maxn];
ll dp[maxn];

void mult(ll a[][maxn],ll b[][maxn]){
    memset(tmp,0,sizeof(tmp));
    for(int i=1; i<=100; i++){
        for(int j=1; j<=100; j++){
            for(int k=1; k<=100; k++){
                tmp[i][j] = (tmp[i][j] + a[i][k]*b[k][j]%mod)%mod;
            }
        }
    }
    for(int i=1; i<=100; i++){
        for(int j=1; j<=100; j++){
            a[i][j] = tmp[i][j];
        }
    }
}

void qpow(ll a[][maxn],ll N){
    memset(res,0,sizeof(res));
    for(int i=1; i<=100; i++){
        res[i][i] = 1;
    }
    while(N){
        if(N&1) mult(res,a);
        mult(a,a);
        N>>=1;
    }
    for(int i=1; i<=100; i++){
        for(int j=1; j<=100; j++){
            a[i][j] = res[i][j];
        }
    }
}

int main(){
    scanf("%lld%d",&n,&m);
    for(int i=0; i<m; i++){
        scanf("%d",&x);
        a[x] = 1;
    }
    scanf("%d",&m);
    for(int i=0; i<m; i++){
        scanf("%d",&x);
        b[x] = 1;
    }
    a &= b;

    for(int i=1; i<=100; i++){
        if(a[i]) g[1][i]=1;
    }
    for(int i=2; i<=100; i++){
        g[i][i-1] = 1;
    }

    // dp[0] = 1;
    // for(int i=0; i<=100; i++){
    //     for(int j=1; j<=i; j++){
    //         if(a[j]){
    //             dp[i] = (dp[i] + dp[i-j] )%mod;
    //         }
    //     }
    // }
    // if(n<=99) printf("%d
", dp[n]);
    // else{
    //     qpow( g ,n-99);
    //     ll ans = 0;
    //     for(int i=1; i<=100; i++){
    //         ans = (ans + dp[100-i]*g[1][i]%mod) %mod;
    //     }
    //     printf("%lld
", ans);
    // }

    //原来直接矩阵快速幂就可以啊.. 因为f(1)=0,然后当作第一位来直接做
    qpow(g,n-0);
    printf("%lld
", g[1][1]);
}