本文参考了该博客的实例,但该博客中的朴素贝叶斯公式计算错误,评论中的也不对,所以,重新写一篇。
原文链接:带你彻彻底底搞懂朴素贝叶斯公式
更多参考:朴素贝叶斯算法原理小结
一. 朴素贝叶斯
朴素贝叶斯中的朴素一词的来源就是假设各特征之间相互独立。这一假设使得朴素贝叶斯算法变得简单,但有时会牺牲一定的分类准确率。
首先给出贝叶斯公式: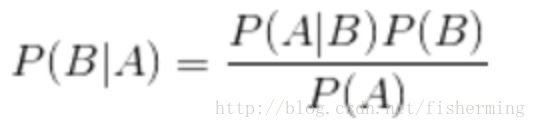
换成分类任务的表达式: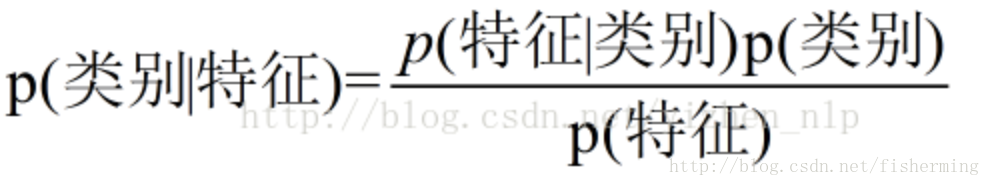
我们最终求的p(类别|特征)即可!就相当于完成了我们的任务。
二. 实例解析
首先,给出数据如下:
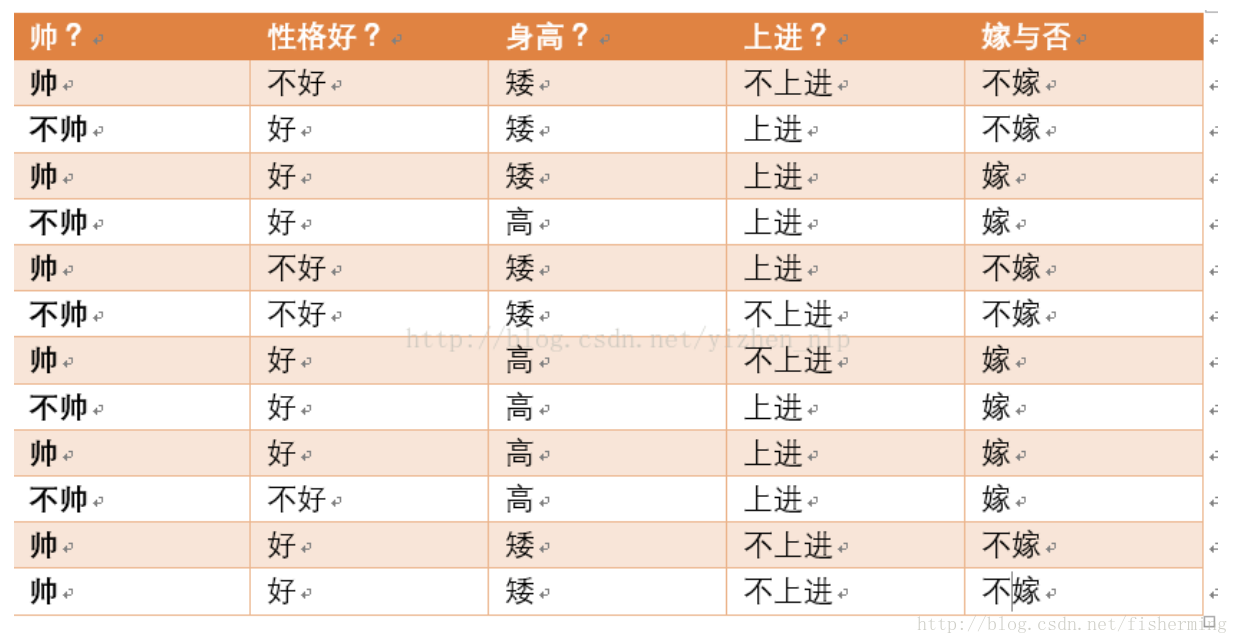
现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
这是典型的二分类问题,按照朴素贝叶斯的求解,转换为P(嫁|不帅、性格不好、矮、不上进)和P(不嫁|不帅、性格不好、矮、不上进)的概率,最终选择嫁与不嫁的答案。
这里我们根据贝特斯公式:

由此,我们将(嫁|不帅、性格不好、矮、不上进)转换成三个可求的P(嫁)、P(不帅、性格不好、矮、不上进|嫁)、P(不帅、性格不好、矮、不上进)。进一步分解可以得:
P(不帅、性格不好、矮、不上进)=P(嫁)P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)+P(不嫁)P(不帅|不嫁)P(性格不好|不嫁)P(矮|不嫁)P(不上进|不嫁)。
P(不帅、性格不好、矮、不上进|嫁)=P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)
将上面的公式整理一下可得:

P(嫁)=1/2、P(不帅|嫁)=1/2、P(性格不好|嫁)=1/6、P(矮|嫁)=1/6、P(不上进|嫁)=1/6。
P(不嫁)=1/2、P(不帅|不嫁)=1/3、P(性格不好|不嫁)=1/2、P(矮|不嫁)=1、P(不上进|不嫁)=2/3
但是由贝叶斯公式可得:对于目标求解为不同的类别,贝叶斯公式的分母总是相同的。所以,只求解分子即可: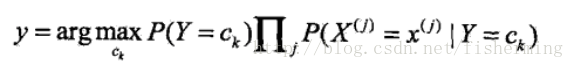
于是,对于类别“嫁”的贝叶斯分子为:P(嫁)P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)=1/2 * 1/2 * 1/6 * 1/6 * 1/6=1/864
对于类别“不嫁”的贝叶斯分子为:P(不嫁)P(不帅|不嫁)P(性格不好|不嫁)P(矮|不嫁)P(不上进|不嫁)=1/2 * 1/3 * 1/2 * 1* 2/3=1/18。
经代入贝叶斯公式可得:P(嫁|不帅、性格不好、矮、不上进)=(1/864) / (1/864+1/18)=1/49=2.04%
P(不嫁|不帅、性格不好、矮、不上进)=(1/18) / (1/864+1/18)=48/49=97.96%
则P(不嫁|不帅、性格不好、矮、不上进) > P(嫁|不帅、性格不好、矮、不上进),则该女子选择不嫁!
三. 朴素贝叶斯的优缺点
优点:
(1) 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
(2)分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
缺点:
朴素贝叶斯假设属性之间相互独立,这种假设在实际过程中往往是不成立的。在属性之间相关性越大,分类误差也就越大。
四. 朴素贝叶斯实战
sklearn中有3种不同类型的朴素贝叶斯:
高斯分布型:用于classification问题,假定属性/特征服从正态分布的。
多项式型:用于离散值模型里。比如文本分类问题里面我们提到过,我们不光看词语是否在文本中出现,也得看出现次数。如果总词数为n,出现词数为m的话,有点像掷骰子n次出现m次这个词的场景。
伯努利型:最后得到的特征只有0(没出现)和1(出现过)。
4.1 我们使用iris数据集进行分类
from sklearn.naive_bayes import GaussianNB from sklearn.model_selection import cross_val_score from sklearn import datasets iris = datasets.load_iris() gnb = GaussianNB() scores=cross_val_score(gnb, iris.data, iris.target, cv=10) print("Accuracy:%.3f"%scores.mean())
输出: Accuracy:0.953
4.2 Kaggle比赛之“旧金山犯罪分类预测”
题目数据:第一种获取方式:Kaggle网站上;第二种获取方式:百度网盘
题目背景:『水深火热』的大米国,在旧金山这个地方,一度犯罪率还挺高的,然后很多人都经历过大到暴力案件,小到东西被偷,车被划的事情。当地警方也是努力地去总结和想办法降低犯罪率,一个挑战是在给出犯罪的地点和时间的之后,要第一时间确定这可能是一个什么样的犯罪类型,以确定警力等等。后来干脆一不做二不休,直接把12年内旧金山城内的犯罪报告都丢带Kaggle上,说『大家折腾折腾吧,看看谁能帮忙第一时间预测一下犯罪类型』。犯罪报告里面包括日期,描述,星期几,所属警区,处理结果,地址,GPS定位等信息。当然,分类问题有很多分类器可以选择,我们既然刚讲过朴素贝叶斯,刚好就拿来练练手好了。
(1) 首先我们来看一下数据
import pandas as pd import numpy as np from sklearn import preprocessing from sklearn.metrics import log_loss from sklearn.cross_validation import train_test_split train = pd.read_csv('/Users/liuming/projects/Python/ML数据/Kaggle旧金山犯罪类型分类/train.csv', parse_dates = ['Dates']) test = pd.read_csv('/Users/liuming/projects/Python/ML数据/Kaggle旧金山犯罪类型分类/test.csv', parse_dates = ['Dates'])
train.csv数据:

我们依次解释一下每一列的含义:
Date: 日期
Category: 犯罪类型,比如 Larceny/盗窃罪 等.
Descript: 对于犯罪更详细的描述
DayOfWeek: 星期几
PdDistrict: 所属警区
Resolution: 处理结果,比如说『逮捕』『逃了』
Address: 发生街区位置
X and Y: GPS坐标
train.csv中的数据时间跨度为12年,包含了将近90w的记录。另外,这部分数据,大家从上图上也可以看出来,大部分都是『类别』型,比如犯罪类型,比如星期几。
2)特征预处理
sklearn.preprocessing模块中的 LabelEncoder函数可以对类别做编号,我们用它对犯罪类型做编号;pandas中的get_dummies( )可以将变量进行二值化01向量,我们用它对”街区“、”星期几“、”时间点“进行因子化。
#对犯罪类别:Category; 用LabelEncoder进行编号 leCrime = preprocessing.LabelEncoder() crime = leCrime.fit_transform(train.Category) #39种犯罪类型 #用get_dummies因子化星期几、街区、小时等特征 days=pd.get_dummies(train.DayOfWeek) district = pd.get_dummies(train.PdDistrict) hour = train.Dates.dt.hour hour = pd.get_dummies(hour) #组合特征 trainData = pd.concat([hour, days, district], axis = 1) #将特征进行横向组合 trainData['crime'] = crime #追加'crime'列 days = pd.get_dummies(test.DayOfWeek) district = pd.get_dummies(test.PdDistrict) hour = test.Dates.dt.hour hour = pd.get_dummies(hour)
特征预处理后,训练集feature,如下图所示:
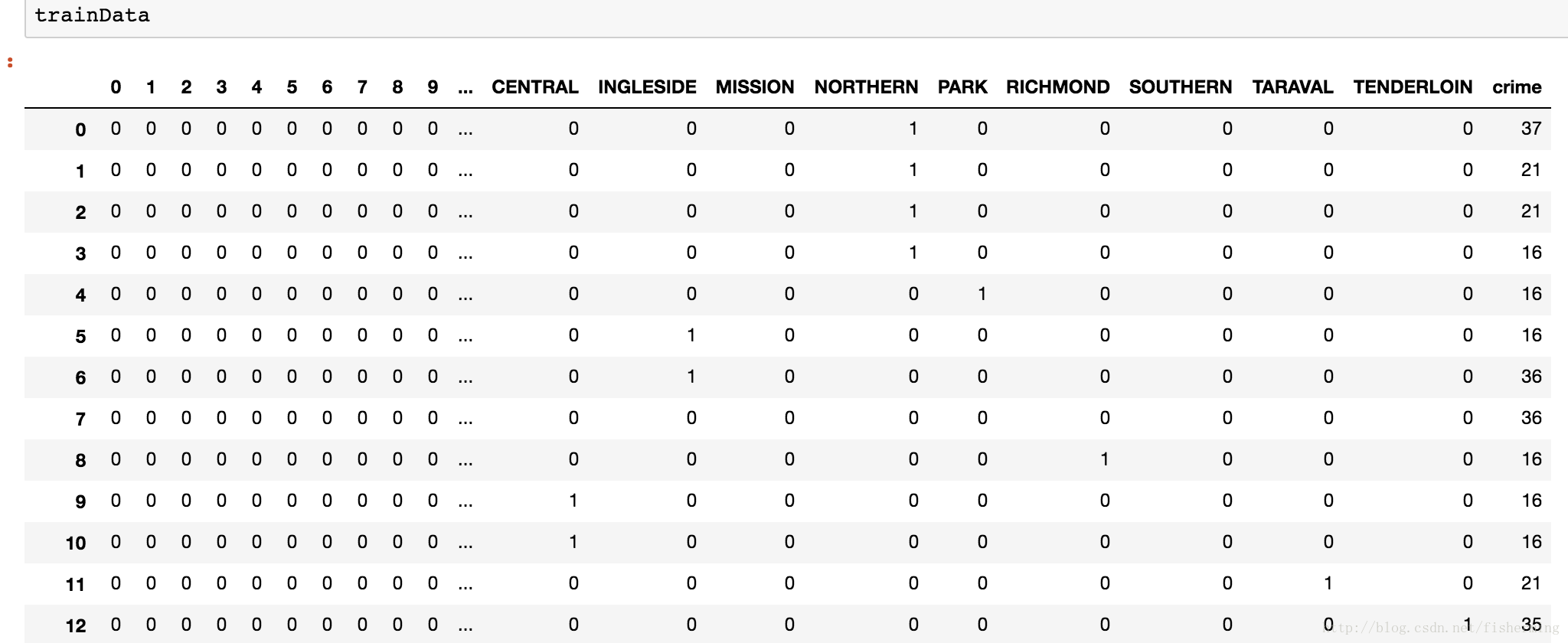
3) 建模
from sklearn.naive_bayes import BernoulliNB import time features=['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday', 'BAYVIEW', 'CENTRAL', 'INGLESIDE', 'MISSION', 'NORTHERN', 'PARK', 'RICHMOND', 'SOUTHERN', 'TARAVAL', 'TENDERLOIN'] X_train, X_test, y_train, y_test = train_test_split(trainData[features], trainData['crime'], train_size=0.6) NB = BernoulliNB() nbStart = time.time() NB.fit(X_train, y_train) nbCostTime = time.time() - nbStart #print(X_test.shape) propa = NB.predict_proba(X_test) #X_test为263415*17; 那么该行就是将263415分到39种犯罪类型中,每个样本被分到每一种的概率 print("朴素贝叶斯建模%.2f秒"%(nbCostTime)) predicted = np.array(propa) logLoss=log_loss(y_test, predicted) print("朴素贝叶斯的log损失为:%.6f"%logLoss)
输出:
朴素贝叶斯建模0.55秒
朴素贝叶斯的log损失为:2.582561
