★实验任务
小 F 很爱打怪,今天因为系统 bug,他提前得知了 n 只怪的出现顺序以及击 倒每只怪得到的成就值 ai。设第一只怪出现的时间为第 1 秒,这个游戏每过 1 秒 钟出现一只新怪且没被击倒的旧怪消失。小 F 决定发动一次技能,他的技能最多 维持 k 秒,他希望获得最大的成就值,请你帮他计算他发动技能的时间 l 和技能 结束时间 r(r-l+1<=k)。当存在多种方案使得成就值最大时,选择技能发动时间 l 最小的方案,再选择技能持续时间 r-l+1 最小的方案。
★数据输入
输入第一行为两个正整数 n(1<=n<=100000),k(0<k<=n),表示出现 n 只怪, 小 F 的技能最多维持 k 秒。 输入第二行为 n 个整数,表示小 F 击倒第 i 秒钟出现的怪能给有获得的成就 值 ai(-1000<=a[i]<=1000)。
★数据输出
输出为一行三个数。第一个数为可获得的最大成就值,第二个数为技能发动 时间 l,第三个数为技能结束时间 r。
| 输入示例 | 输出示例 |
|---|---|
| 6 3 -1 2 -6 5 -5 6 |
6 4 6 |
| 输入示例 | 输出示例 |
|---|---|
| 5 5 -1 -1 -1 -1 -1 |
-1 1 1 |
★思路
这道题的目标就是找到长度不超过k的最大子序列和,求子序列和可以使用前缀和与后缀和的思想。如果先使用前缀和做法,把数组倒序就是后缀和做法。
前缀和的概念就是第i个数前面所有数字的和。所以[l,r]区间的和可以写成。(sum[r]-sum[l])。
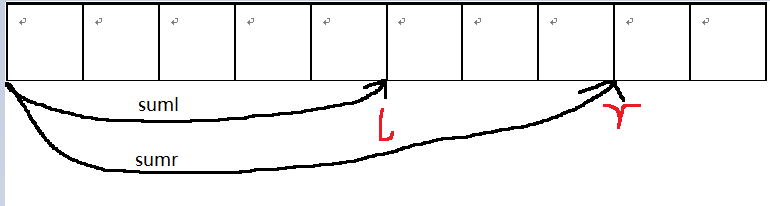
这样子要找到数字i前面不超过k长度的最大子序列和,就要找到它前面k个前缀和的最小值。(因为sum[i]为定值)。
要找到sum[i]前面k个前缀和的最小值做法是,用递增队列。
建立结构体数组来模拟这个过程。
struct intt
{
int value;
int pos; //记录位置,判断长度是否超过k
int start;
};
首先队首元素存0(因为sum[1]前面没以有元素,所以sum[0]=0)。
接下来对于每一个sum[i],先用它去减队首元素(队首元素代表第i个数前面的最小前缀和)。然后把它加入队列。
如果它比它前面的数字值小,就把它前面的元素弹出(这相当于更新当前的最小值)。
如果它比它前面的数字大,就把它留起来备用。因为他前面的数字最多可以使用k次,如果他前面元素使用k次被弹出后,就要用它来补充当前最小前缀和这个位置了。
如果它与前面元素相等的话,也要弹出前面元素,因为前面元素已经被使用它过一次了,而它没有被使用过。
这样子我们找到的是每个数字i所对应的起始位置比较靠后的满足条件的最大子区间和。如果我们把数组倒序进行这个操作那么我们就找到了满足题目要求的“当存在多种方案使得成就值最大时,选择技能发动时间 l 最小的方案,再选择技能持续时间 r-l+1 最小的方案”。
★Code
#include<iostream>
#include<string.h>
using namespace std;
struct intt
{
int value;
int pos;
int start;
};
int a[100005]; //普通的数组
intt dp[100005]; //模拟队列,队首元素代表最小前缀和
intt sum[100005]; //前缀和数组
intt mmax[100005]; //以i结尾符合条件的区间最大和
int main()
{
int n, k, i;
intt *head = &dp[0];
intt *tail = &dp[0];
scanf("%d %d",&n,&k);//cin >> n >> k;
memset(a, 0, sizeof(a));
memset(dp, 0, sizeof(dp));
memset(sum, 0, sizeof(sum));
memset(mmax, 0, sizeof(mmax));
for (i = n; i >= 1; i--)
{
scanf("%d",&a[i]);// cin >> a[i];
}
for (i = 1; i <= n; i++)
{
sum[i].value = sum[i - 1].value + a[i];
sum[i].pos = i;
}
for (i = 1; i <= n; i++)
{
if (tail->pos - head->pos >= k)
head++;
mmax[i].value = sum[i].value - head->value;
mmax[i].start = head->pos;
// cout<<mmax[i].start<<endl;
while (1)
{
if (sum[i].value>tail->value)
{
tail++;
tail->value = sum[i].value;
tail->pos = i;
break;
}
else if (sum[i].value == tail->value)
{
tail->pos = i;
break;
}
else
{
if (tail == head)
{
tail->value = sum[i].value;
tail->pos = sum[i].pos;
break;
}
else
{
tail->value = 0;
tail->pos = 0;
tail--;
}
}
}
}
/*for(int i=1;i<=n;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
for(int i=1;i<=n;i++)
{
cout<<mmax[i].value<<" ";
}
cout<<endl;*/
int maxx = mmax[1].value;
for (i = 1; i <= n; i++)
{
if (mmax[i].value>maxx)
maxx = mmax[i].value;
}
int temp;
for (i = n; i >= 1; i--)
{
if (mmax[i].value == maxx)
{
temp = i;
break;
}
}
int flag = temp;
int tempp = maxx;
while (1)
{
tempp -= a[flag];
if (!tempp)
break;
flag--;
}
printf("%d %d %d", maxx, n + 1 - temp, n + 1 - flag);
//cout << maxx << " " << n + 1 - temp << " " << n + 1 - flag;
return 0;
}