1.本周学习总结
1.思维导图
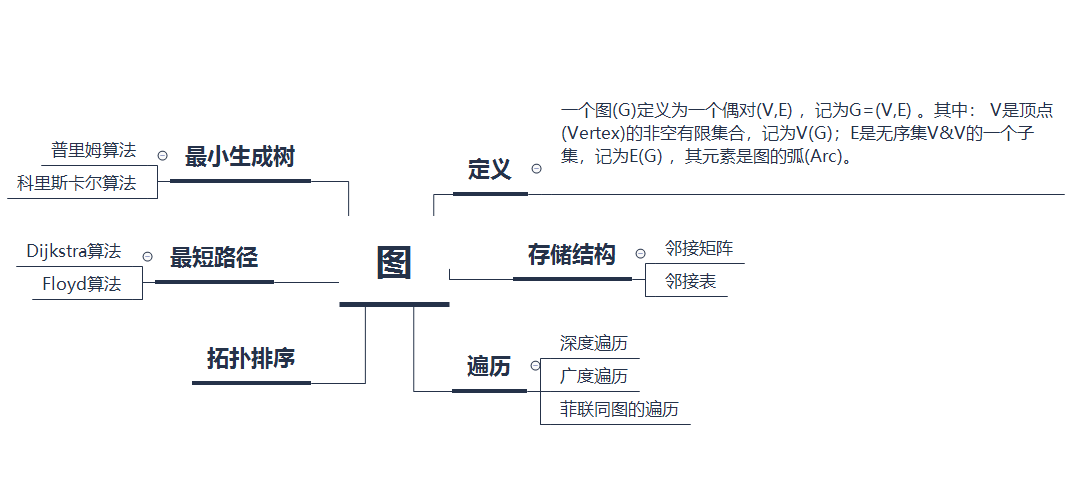
2.谈谈你对图结构的认识及学习体会。
- 图是一种比线性表和树更为复杂的数据结构,是研究数据元素之间的多对多的关系。在这种结构中,任意两个元素之间可能存在关系。即结点之间的关系可以是任意的,图中任意元素之间都可能相关。图结构由两个集合点和边构成。图的遍历分为深度遍历和广度遍历。算法上有Dljkstra算法,Floyd算法。
- 对于我个人而言,邻接矩阵可以用二维数组来做,邻接表结构是好理解,但结构体的定义还是有一些复杂。且图的算法种类比较多,有一些复杂,记忆比较困难。对于代码实在不够熟悉,理论知识上课是理解了,课上的互动也可以比较完整的解答,总体理解还可以,就是下了课,容易忘记,但是对于代码的编写实在过于粗糙。
2.PTA实验作业(6分)
2.1题目1:图着色问题
2.1.1伪代码
定义整型 n,e,vcolor,count,g[600][600], color[600]
int Dudge()
定义 i,j
i from1 to n
j from1 to n
if(g[i][j]==1&&color[i]==color[j])
return 0
return 1
int main()
int v,re,nowColor, k[600], flag
输入n,e,vcolor
格式化 g
i from1 to e
输入v,re
g[v][re]=g[re][v]=1;
输入count
while(count--)
格式化k
nowColor=0
flag=1
i from1 to n
输入color[i]
if(k[color[i]]==0)
nowColor++
k[color[i]]++;
if(nowColor==vcolor)
flag=0;
if(Dudge()==1&&flag==0)
输出Yes
else
输出No
2.1.2代码截图
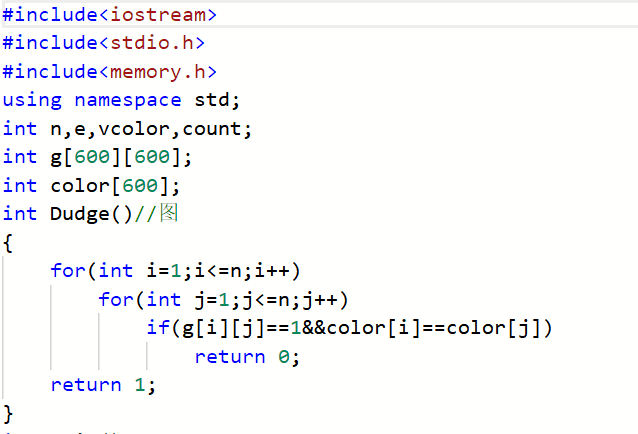
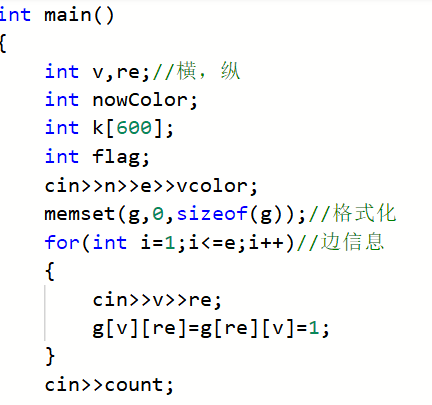

2.1.3本题PTA提交列表说明。

- 数组定义时空间定义过小,出现了段错误
2.2 题目2六度空间
2.2.1伪代码
宏定义 maxn 10000
定义整型 N, M, visit[maxn], arr[maxn][maxn];
int BFS(int v)
queue<int> q;
定义整型 temp, level = 0, tail, last = v, count = 1;
q.push(v);
visit[v] = 1;
while q不为空
temp = q.front();
q.pop();
i from1 to N
if (arr[temp][i] &&visit[i] == 0)
count++;
tail = i;
visit[i] = 1;
if (temp == last)
level++ last = tail
if (level == 6) break
return count;
int main()
输入N,M
定义a, b;
i from1 to M
输入a,b
arr[a][b] = 1;
arr[b][a] = 1;
i from1 to N
int cnt = BFS(i);
memset(visit, 0, sizeof(visit));
double f = 100.00*cnt / N;
输出
return 0;
2.2.2代码截图
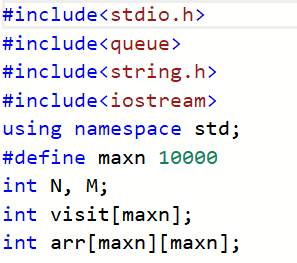
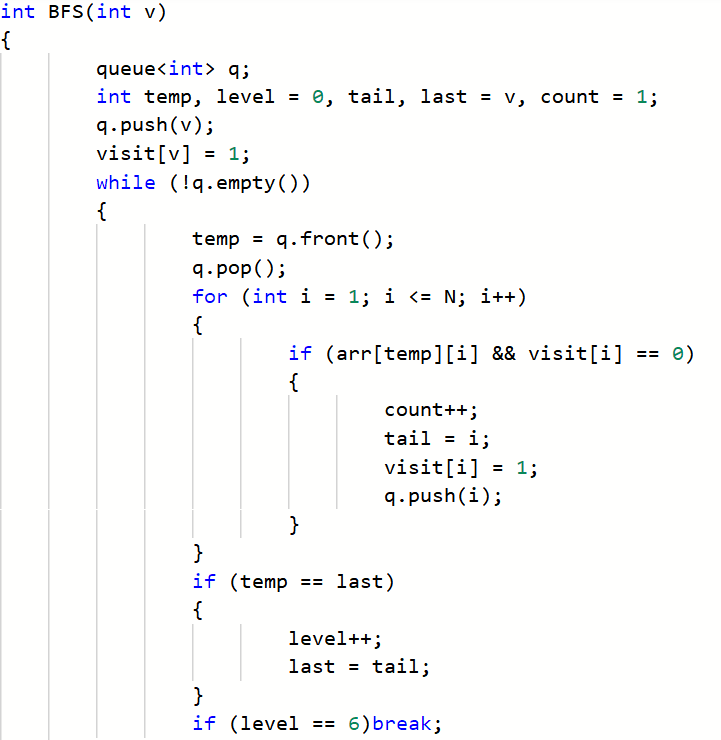

2.2.3本题PTA提交列表说明。

 判断条件有误,是并而非或
判断条件有误,是并而非或 循环条件有问题,应为N
循环条件有问题,应为N
2.3 题目3公路村村通
2.3.1伪代码
宏定义 MAXVEX 1003, INF 65535
int main()
定义cost = 0,v,e
输入v,e
CreateGraph(v,e);
cost =Prim(v,e);
输出cost;
return 0;
void CreateGraph(int v,int e)
定义 i,j, v1,v2,w
i from 1 to v
j from 1 to v
G[i][j] = INF
i from 0 to v
输入v1,v2,w
G[v1][v2] = w
G[v2][v1]= G[v1][v2]
int Prim(int v,int e)
定义 min, i,j,k, lowcost[MAXVEX],cost =0;
初始化lowcost[1] = 0
i from 2 to v
lowcost[i] = G[1][i];
i from 2 to v
min = INF
j = 1
k = 0
while( j<=v )
if( lowcost[j]!=0 && lowcost[j]<min)
min = lowcost[j];
k = j
j++
if(k==0)
不连通return -1
cost =cost+min
lowcost[k] = 0
j from 2 to v
if( lowcost[j]!=0 && G[k][j]<lowcost[j])
lowcost[j] = G[k][j];
return cost;
2.3.2代码截图
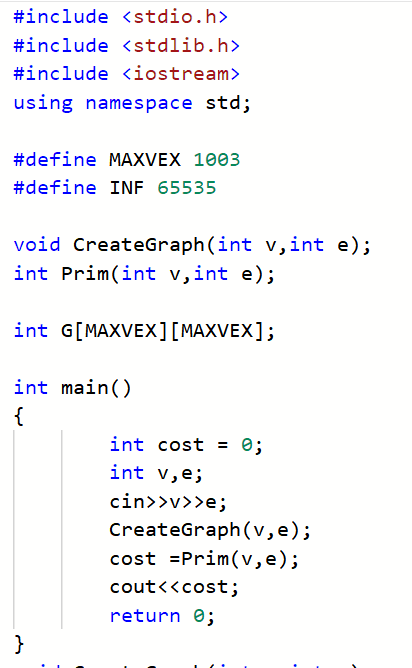
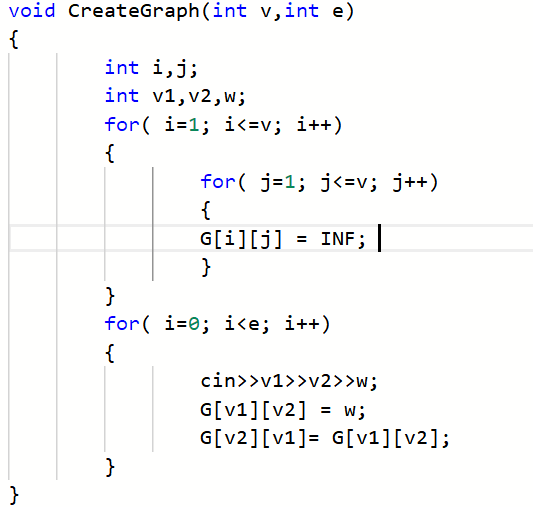
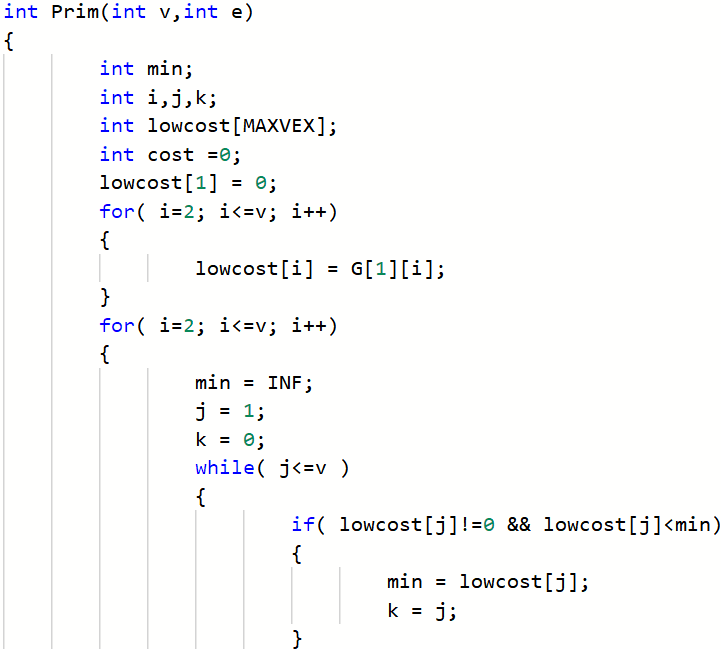

2.3.3本题PTA提交列表说明。

- Prim函数忘记return,导致答案错误。
3、上机考试错题及处理办法
3.1最短路径
3.1.1截图错题代码

3.1.2 错的原因及处理方法
- 原因:就是挣点测试分
- 处理方法:运用Dijksra算法
判断是否已存入该点到S集合中
i from 1 to n
dist[i] = A[v0][i];
S[i] = false;
if(dist[i] == MAXINT)
prev[i] = -1;
else
prev[i] = v0;
dist[v0] = 0;
S[v0] = true;
i from 2 to n
定义 mindist = MAXINT;,u = v0
j from 1 to n
找出当前未使用的点j的dist[j]最小值并用u保存当前邻接点中距离最小的点的号码
S[u] = true;
j from 1 to n
通过新加入的u点路径找到离v0点更短的路径
更新dist
记录前驱顶点
3.2图邻接表操作
3.2.1截图错题代码
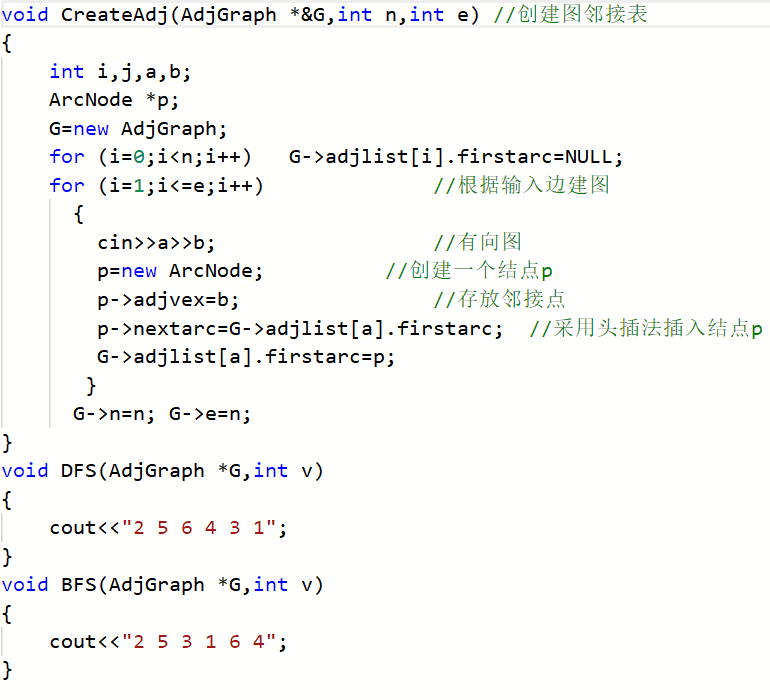
3.2.2 错的原因及处理方法
- 原因:就是挣点测试分
- 思路
先建表
void DFS(AdjGraph *G,int v)
ArcNode *p,visited[v]=1,flag++;
输出v
如果flag没有到达长度 输出空格
p=G->adjlist[v].firstarc;
while p不为空
if(visited[p->adjvex]==0)
DFS(G,p->adjvex)
p=p->nextarc
void BFS(AdjGraph *G,int v)
flag=0,ArcNode *p;
定义queue[MAXV],front=0,rear=0;
visited[v]=1,flag++,queue[rear]=v;
输出v和空格
while(front<=rear)
p=G->adjlist[queue[front]].firstarc;
while p不为空
if(visited[p->adjvex]==0)
flag++;
输出p->adjvex;
if(flag!=G->n) 输出空格
visited[p->adjvex]=1;
queue[++rear]=p->adjvex;
p=p->nextarc;
front++;
3.3拓扑排序
3.3.1截图错题代码
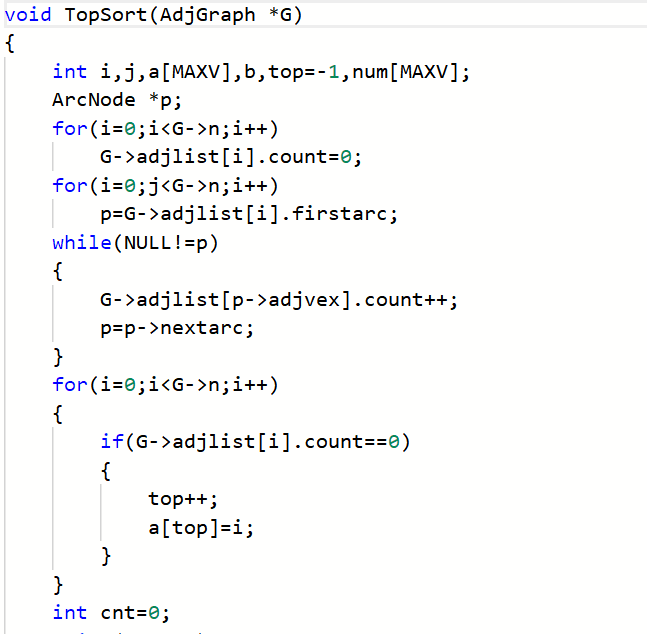


3.3.2 错的原因及处理方法
- 原因
 在最后的循环里应该是cnt-1,但是写成了cnt
在最后的循环里应该是cnt-1,但是写成了cnt - 处理方法:修改for循环的长度
3.4六度空间
3.4.1截图错题代码
没有写该代码
3.4.2 错的原因及处理方法
- 思路:
3.5公路村村通
3.5.1截图错题代码

3.5.2 错的原因及处理方法
- 凑测试点
- 思路:
int minDist(int dist[],bool flag[],int n) //求最小的dist
int mindist = MAXNUM;
int icount = NOEXIT;
for(int i=1;i<n;i++)
if(dist[i] < mindist && flag[i] == false)
icount = i;
mindist = dist[i];
return icount;
int Prim(int *data[], int n, int m)
建int型的sta栈
sta.push(0);
定义 *dist = new int[n];
i from 0 to n
用dist记录长度MAXNUM
dist[1] = 0;
bool *collected = new bool[n];
i from 0 to n
collected标记是否被访问false
int *parent = new int[n];
i from 0 to n
parent记录树的结构NOEXIT
定义 output = 0;
while (1)
int V = minDist(dist, collected, n);
if (V == NOEXIT)
break;
sta.push(V);
output += dist[V];
dist[V] = 0;
collected[V] = true;
W from 1 to n
如果W是V的邻接点并且W没有被访问
dist[W] = data[V][W];
parent[W] = V;
if(sta.size() != n)
return NOEXIT;
else
return output;
int main()
{
输入n,m
n++;
用邻接矩阵存储图
输出Prim(data,n,m) 并换行
return 0;
3.6天梯地图
3.6.1截图错题代码
3.6.2 错的原因及处理方法
- 思路:
void InitGraph(int N, int M) //创建并初始化地图
i from 0 to N
j from 0 to N
sum[j] = 0;
初始化各点间的距离和时间均为无穷大
定义 v1, v2, way, length, time
i from 0 to M
读取输入创建地图
如果不是单行线,两地可互通
Graph[v2][v1].length = length;
Graph[v2][v1].time = time;
void InitVisit(int N, int S)
i from 0 to N
将 LVisit[i].visit = 0初始化为未访问
根据地图 LVisit[i].length = Graph[S][i].length初始化到原点距离
将TVisit[i].visit = 0初始化为未访问
根据地图TVisit[i].time = Graph[S][i].time初始化时间
如果和原点相通设置前驱点为原点,并设置个时间点到原点距离
设置原点LVisit[S].visit = 1,TVisit[S].visit = 1已访问
void DST_L(int N, int S)
{
j from 1 to N
设置N点为最近点,N点已设为无穷远
i from 0 to N
求出最近点并设置为已访问
LVisit[mlpoint].visit = 1
i from 0 to N
if(!LVisit[i].visit)
更新为短的距离
if(LVisit[i].length>LVisit[mlpoint].length+Graph[mlpoint][i].length)
更新为更短的距离
设置前驱点
else if(LVisit[i].length==LVisit[mlpoint].length+Graph[mlpoint][i].length){
int l1=0,l2=0;
int pre = LVisit[i].pre;
while(pre!=S)
l1计算结点
pre = mlpoint;
while(pre!=S)
l2计算节点
如果节点多则更新
void DST_T(int N, int S)
j from 1 to N
/无穷为最短点
i from 0 to N
求出最短点并设置为已访问
TVisit[mtpoint].visit = 1;
i from 0 to N
if(!TVisit[i].visit){
更新最短时间
if(TVisit[i].time>TVisit[mtpoint].time+Graph[mtpoint][i].time){
更新最短时间的距离
else if(TVisit[i].time==TVisit[mtpoint].time+Graph[mtpoint][i].time){
if(sum[i]>sum[mtpoint]+Graph[mtpoint][i].length)
选距离更短的
更新其距离
int main()
定义并输入 N, M;
初始化并读取输入创建图
定义并输入S, D;
创建并初始化距离、时间、访问表
DST_L(N,S)求最短距离
DST_T(N,S)求最短时间
定义 lpath[601]最短距离路径表
定义tpath[601]最短时间路径表
定义l=600, t=600,pre = D;
while(pre!=S)
l根据目的地不断往后后移,直到后移到原点
pre = D;
while(pre!=S)
t根据目的地不断往后后移,直到后移到原点
如果路径t,l长度一样
int flag = 0;
for(int i=t+1; i<601; i++)
判断路径是否完全相同,如果不同
flag = 1;
if(flag == 1)路径不同
输出"Time = "Visit[D].time": "<<S
i from t+1 to 601
输出tpath[i]
换行
输出Distance = "<<LVisit[D].length<<": "<<S;
i from l+1 to 601
输出lpath[i];
如果路径相同
输出"Time = "TVisit[D].time; "<<"Distance = "<<LVisit[D].length": "<<S;
i from t+1 to 601
输出tpath[i];
return 0;
输出"Time = "TVisit[D].time": "<<S;
i from t+1 to 601
输出tpath[i];
换行
输出"Distance = "LVisit[D].length": "<<S;
i from l+1 to 601
输出lpath[i];