Sum HDU

分析：

手动打表，发现：(ans=2^{(n-1)}\%mod)。
同时根据欧拉降幂公式：

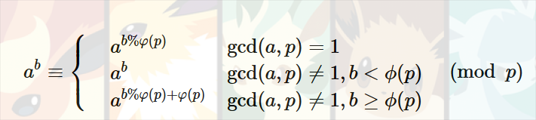
可以发现 (gcd(2,1e9+7)=1)，所以采用第一种形式，直接取模即可。
另外， ((a-1)\%p=(a\%p-1+p)\%p)

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
const int mod=1e9+7;
char ss[N];
ll power(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1)
            res=res*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return res%mod;
}
int main()
{
    while(scanf("%s",ss+1)!=EOF)
    {
        int len=strlen(ss+1);
        ll num=0;
        for(int i=1;i<=len;i++)
        {
            num=num*10+ss[i]-'0';
            num%=(mod-1);
        }
        printf("%lld
",power(2LL,(num%(mod-1)-1+mod-1)%(mod-1)));
    }
    return 0;
}