让你秒懂的快速幂入门教程
我们先来看一个例子:如何计算(2^8)?
首先,你会想到直接把(8)个(2)乘起来,像这样:
[egin{aligned}
2*2&=4 \
4*2&=8 \
8*2&=16 \
16*2&=32 \
32*2&=64 \
64*2&=128 \
128*2&=256
end{aligned}
]
这样需要做7次乘法运算。有没有更快的做法呢?其实还可以这样:
[2^2=4 \
4^2=16=(2^2)^2=2^{2*2}=2^4 \
16^2=256=(2^4)^2=2^{2*2*2}=2^8
]
上面的过程可以形象地理解为:
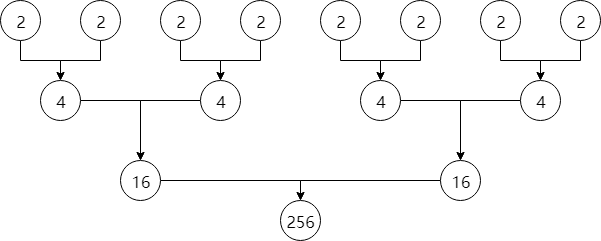
这样只需要做3次乘法运算,就能算出(2^8)的值!
上面这个例子揭示了快速幂算法的核心思想。即,要运算一个数(a)的(2^n)次方,可以将其自乘(n)次,每次指数都会翻倍,这样能够快速算得(a^{2^n})的值。用c++写起来就是这样:
int a=2,n=8;
n=log2(n); //log2()函数定义中头文件<cmath>中,表示以2为底取对数
for(int i=1;i<=n;++i){
a=a*a;
}
那你可能想问了,如果幂指数不是(2)的整数次方,该如何计算呢?以(2^7)为例:
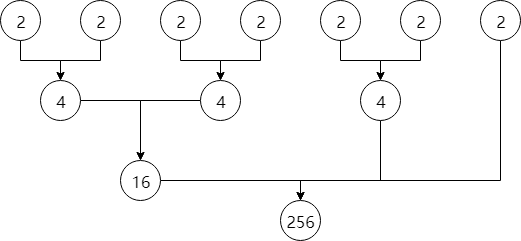
我们只要把指数(7)化为几个(2)的整数次方之和((2^2+2^1+2^0)),再将对应的(2^{2^2},2^{2^1},2^{2^0})乘起来,就能得到(2^7)。
看到这里,机智的你可能发现了什么:把一个十进制数化为几个2的整数次方之和,这不就是进制转换的过程吗?
[(7)_{10}=(111)_{2} \
7=2^2+2^1+2^0
]
二进制,正是计算机最擅长的东西。c++中有&和>>运算符,是针对二进制数进行运算的。
a&b得到a与b按位与的结果,如果将一个数&1,由于1除了末位其余位都是0,与的结果也是0,那么只需考虑末位,如果这个数的末位为1,得到的就是1;如果这个数末位是0,得到的就是0。我们可以用这个方法来判断一个数的二进制末位是否为1。
a>>b得到将数a的二进制都向右移动b位。可以类比十进制,向右移动一位(也就是小数点向左移动一位)表示将这个数除10,二进制中右移一位就是除2。
int quick_power(int a,int n){
int ans=1; //ans要初始化为1
while(n){ //当n不为0时继续进行快速幂
if(n&1){ //若n的二进制末位为1则返回真
//如果n的二进制数第i位为1,说明将幂指数n分解之后会包含2^i
//因此需要将当前计算的a^(2^i)乘进答案
ans=ans*a;
}
n>>=1; //表示将二进制数n左移一位,舍弃最低位
a=a*a; //计算a^(2^i)
}
return ans;
}