Scrambled Polygon
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 7703 | Accepted: 3673 |
Description
A closed polygon is a figure bounded by a finite number of line segments. The intersections of the bounding line segments are called the vertices of the polygon. When one starts at any vertex of a closed polygon and traverses each bounding line segment exactly once, one comes back to the starting vertex.
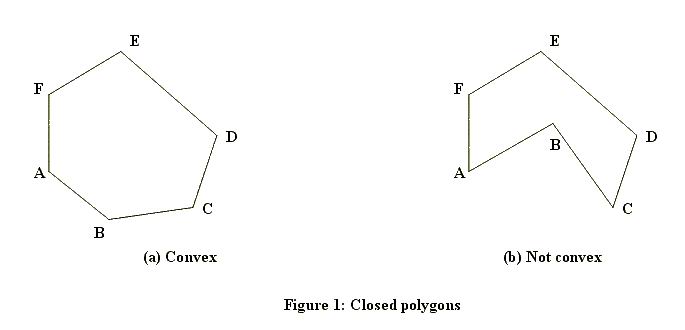
A closed polygon is called convex if the line segment joining any two points of the polygon lies in the polygon. Figure 1 shows a closed polygon which is convex and one which is not convex. (Informally, a closed polygon is convex if its border doesn't have any "dents".)
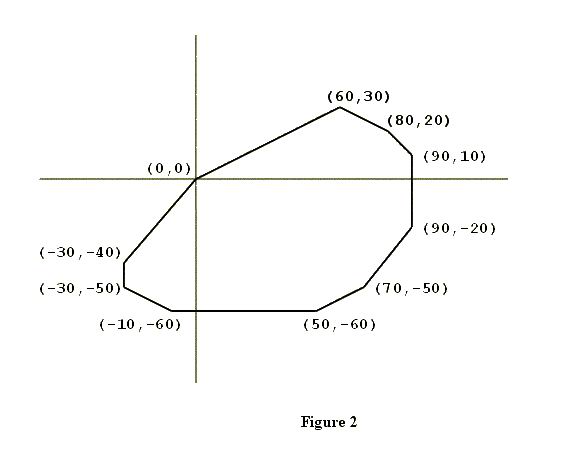
The subject of this problem is a closed convex polygon in the coordinate plane, one of whose vertices is the origin (x = 0, y = 0). Figure 2 shows an example. Such a polygon will have two properties significant for this problem.
The first property is that the vertices of the polygon will be confined to three or fewer of the four quadrants of the coordinate plane. In the example shown in Figure 2, none of the vertices are in the second quadrant (where x < 0, y > 0).
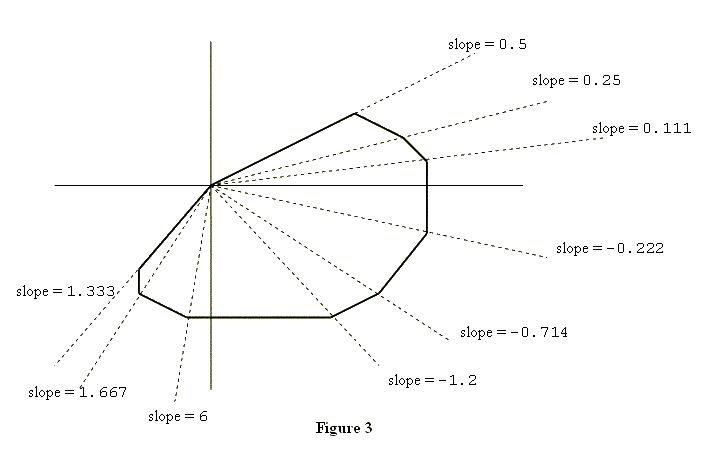
To describe the second property, suppose you "take a trip" around the polygon: start at (0, 0), visit all other vertices exactly once, and arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw the diagonal that connects the current vertex with (0, 0), and calculate the slope of this diagonal. Then, within each quadrant, the slopes of these diagonals will form a decreasing or increasing sequence of numbers, i.e., they will be sorted. Figure 3 illustrates this point.
A closed polygon is called convex if the line segment joining any two points of the polygon lies in the polygon. Figure 1 shows a closed polygon which is convex and one which is not convex. (Informally, a closed polygon is convex if its border doesn't have any "dents".)

The subject of this problem is a closed convex polygon in the coordinate plane, one of whose vertices is the origin (x = 0, y = 0). Figure 2 shows an example. Such a polygon will have two properties significant for this problem.
The first property is that the vertices of the polygon will be confined to three or fewer of the four quadrants of the coordinate plane. In the example shown in Figure 2, none of the vertices are in the second quadrant (where x < 0, y > 0).
To describe the second property, suppose you "take a trip" around the polygon: start at (0, 0), visit all other vertices exactly once, and arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw the diagonal that connects the current vertex with (0, 0), and calculate the slope of this diagonal. Then, within each quadrant, the slopes of these diagonals will form a decreasing or increasing sequence of numbers, i.e., they will be sorted. Figure 3 illustrates this point.


Input
The input lists the vertices of a closed convex polygon in the plane. The number of lines in the input will be at least three but no more than 50. Each line contains the x and y coordinates of one vertex. Each x and y coordinate is an integer in the range -999..999. The vertex on the first line of the input file will be the origin, i.e., x = 0 and y = 0. Otherwise, the vertices may be in a scrambled order. Except for the origin, no vertex will be on the x-axis or the y-axis. No three vertices are colinear.
Output
The output lists the vertices of the given polygon, one vertex per line. Each vertex from the input appears exactly once in the output. The origin (0,0) is the vertex on the first line of the output. The order of vertices in the output will determine a trip taken along the polygon's border, in the counterclockwise direction. The output format for each vertex is (x,y) as shown below.
Sample Input
0 0 70 -50 60 30 -30 -50 80 20 50 -60 90 -20 -30 -40 -10 -60 90 10
Sample Output
(0,0) (-30,-40) (-30,-50) (-10,-60) (50,-60) (70,-50) (90,-20) (90,10) (80,20) (60,30)
Source
有点累。。不多说了。。。直接代码

1 /************************************************************************* 2 > File Name: code/poj/2007.cpp 3 > Author: 111qqz 4 > Email: rkz2013@126.com 5 > Created Time: 2015年11月08日 星期日 19时35分54秒 6 ************************************************************************/ 7 8 #include<iostream> 9 #include<iomanip> 10 #include<cstdio> 11 #include<algorithm> 12 #include<cmath> 13 #include<cstring> 14 #include<string> 15 #include<map> 16 #include<set> 17 #include<queue> 18 #include<vector> 19 #include<stack> 20 #include<cctype> 21 #define fst first 22 #define sec second 23 #define lson l,m,rt<<1 24 #define rson m+1,r,rt<<1|1 25 #define ms(a,x) memset(a,x,sizeof(a)) 26 using namespace std; 27 const double eps = 1E-8; 28 const int dx4[4]={1,0,0,-1}; 29 const int dy4[4]={0,-1,1,0}; 30 typedef long long LL; 31 const int inf = 0x3f3f3f3f; 32 const int N=55; 33 int cnt; 34 int dblcmp(double d) 35 { 36 return d<-eps?-1:d>eps; 37 } 38 struct point 39 { 40 double x,y; 41 point(){} 42 point(double _x,double _y): 43 x(_x),y(_y){}; 44 bool input() 45 { 46 return scanf("%lf %lf",&x,&y)!=EOF; 47 } 48 point operator - (const point &p)const 49 { 50 return point(x-p.x,y-p.y); 51 } 52 53 double operator^(const point &p)const 54 { 55 return x*p.y-y*p.x; 56 } 57 }p[N]; 58 59 bool cmp(point a,point b) 60 { 61 point c; 62 c.x=0.0; 63 c.y=0.0; 64 double tmp =(a-c)^(b-c); 65 // cout<<"tmp:"<<tmp<<endl; 66 return tmp>0; 67 } 68 int main() 69 { 70 #ifndef ONLINE_JUDGE 71 freopen("in.txt","r",stdin); 72 #endif 73 cnt = 0 ; 74 while (p[cnt].input()) cnt++; 75 76 sort(p+1,p+cnt,cmp); 77 for ( int i = 0 ; i < cnt ; i++) printf("(%.0f,%.0f) ",p[i].x,p[i].y); 78 79 80 81 #ifndef ONLINE_JUDGE 82 #endif 83 fclose(stdin); 84 return 0; 85 }
