一.思维导图
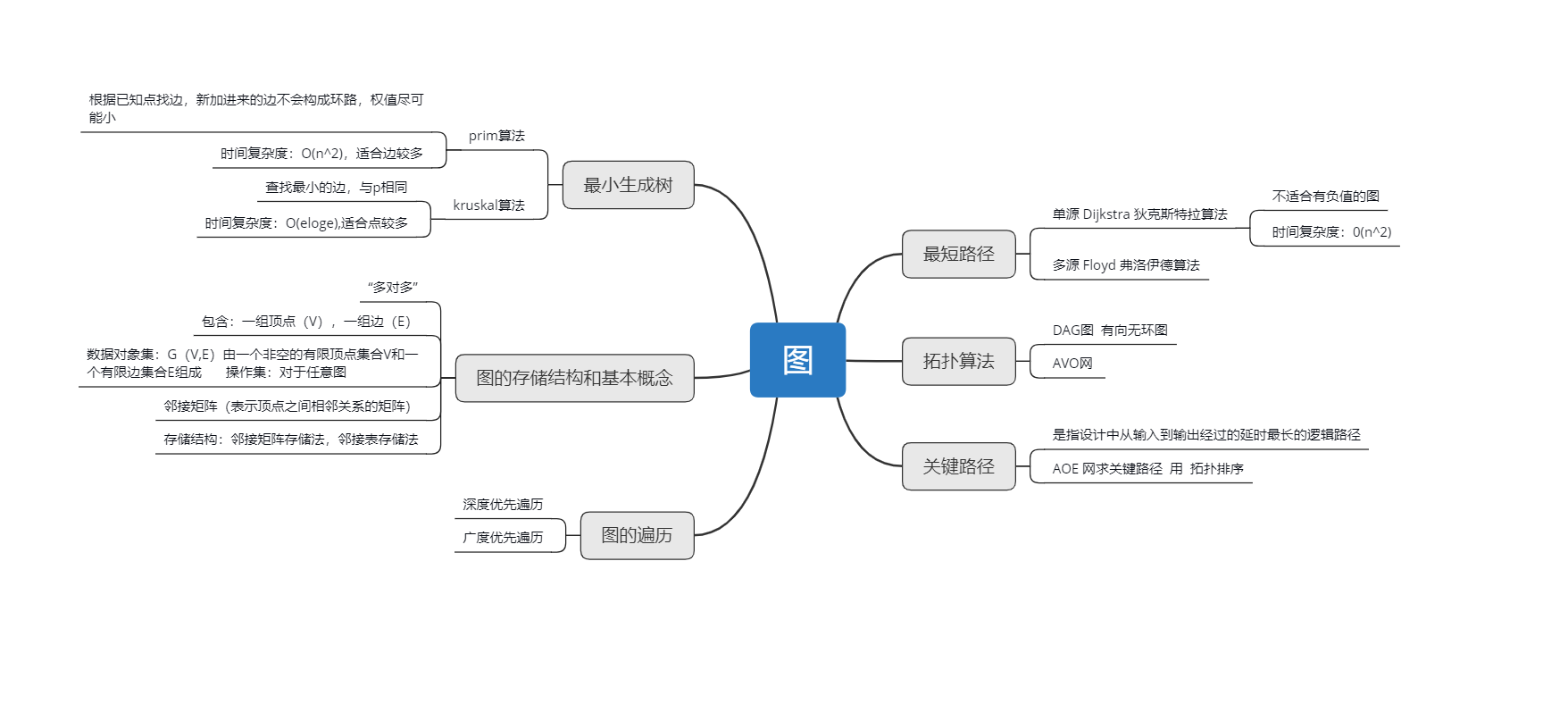
二.重要概念的笔记
1.图的定义:
图是由一些点和这些点之间的连线所组成的,其中,点通常称为顶点,而点到点之间的连线通常称之为边或者弧。通常记为G=(V,E);
2.
含有 e=n(n-1)/2条边的无向图称作###完全图;
含有 e=n(n-1)条弧的有向图称作###有向完全图;
若边或弧的个数 e<nlog2n,则称作###稀疏图,否则称作###稠密图。
3.生成树和最小生成树
生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。
4.图的遍历:
从给定图中任意指定的顶点(称为初始点)出发,按照某个搜索方法沿着图的边访问图中的所有顶点,使每个顶点仅被访问一次的过程。
(1)深度优先遍历(DFS):
从图中某个顶点v出发,访问此顶点,然后从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。
(2)广度优先遍历(BFS):
类似于树的层次遍历。
DFS和BFS:
(1)空间复杂度相同,都为O(n);时间复杂度只与存储结构有关,而与搜索路径无关
(2)DFS求出的路径不一定是最短路径,BFS一定是最短路径
5.最短路径
求每一对顶点之间的最短路径:每次以一个顶点为源点,重复执行Dijkstra算法n次,时间复杂度为O(n3);弗洛伊德(Floyd)算法:时间复杂度也是O(n3)。
6.关键路径
求ve的顺序应该是按拓扑有序的次序;求vl的顺序应该是按拓扑逆序的次序
三.疑难解答及解决方案
对普里姆算法(prim)和克鲁斯卡尔算法(kruskal)不太清楚。
解决方法:
通过看老师的文件及百度来掌握。
都是用来求图的最小生成树
Kruskal算法思想:直接以边为目标去构建最小生成树
第一步:构造一个只含 n 个顶点的子图 SG;
第二步:从权值最小的边开始,若它的添加不使SG中产生回路,则在 SG 上加上这条边;
第三步:如此重复,直至加上 n-1 条边为止。
Prim算法思想:以某一顶点为起点,一点一点的去找各顶点上最小权值的边来构建最小生成树。
第一步:取图中任意一个顶点 v 作为生成树的根;
第二步:往生成树上添加新的顶点 w。在添加的顶点w和已经在生成树上的顶点v 之间必定存在一条边,并且该边的权值在所有连通顶点 v 和 w 之间的边中取值最小;
第三步:继续往生成树上添加顶点,直至生成树上含有 n 个顶点为止。