NOIP 2015：信息传递

题目描述

有n个同学（编号为1到n）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为i的同学的信息传递对象是编号为Ti同学。

游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息，但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自己的生日时，游戏结束。请问该游戏一共可以进行几轮？

输入输出格式

输入格式：
输入共2行。

第1行包含1个正整数n表示n个人。

第2行包含n个用空格隔开的正整数T1,T2,……,Tn其中第i个整数Ti示编号为i

的同学的信息传递对象是编号为Ti的同学，Ti≤n且Ti≠i

数据保证游戏一定会结束。

输出格式：
输出共 1 行，包含 1 个整数，表示游戏一共可以进行多少轮。

输入输出样例

输入样例#1：
5
2 4 2 3 1

输出样例#1：
3

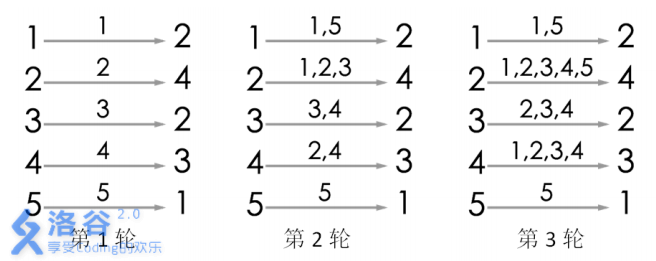
样例解释：

游戏的流程如图所示。当进行完第 3 轮游戏后， 4 号玩家会听到 2 号玩家告诉他自

己的生日，所以答案为 3。当然，第 3 轮游戏后， 2 号玩家、 3 号玩家都能从自己的消息

来源得知自己的生日，同样符合游戏结束的条件。

对于 30%的数据， n ≤ 200；

对于 60%的数据， n ≤ 2500；

对于 100%的数据， n ≤ 200000。

　　芒果君：我先随便说两句~本来说好假期要好好学OI，结果这几天一直在浪，那就从这道题开始我要好好学了的说_(:з」∠)_

　　这道题的题意灰常清楚，在我刚学完floyd后画了个图就看出，这是在求图中长度大于1的最小环。关键是怎么求呢？啥都不会的我一脸懵逼，然后就暂时放弃了。再然后我看了个tarjan算法的B站视频，猛的发现作者居然选了信息传递当例题~再再然后我就跟着他打了一遍……我一直觉得low[i]很迷，其实它就是表示能到达i点的最小编号是多少。（我去，如果我把红字部分换成为i或i的子树能够追溯到的最早的栈中节点的次序号你还能看懂吗），然后进行栈操作计数更新答案就做完了。

　　哦！对啦！其实我觉得这道题的写法还有一个可取的地方就是用了我不会用的vector容器，这也是放到博客上的一个原因，就当开开眼界。（原视频：http://www.bilibili.com/video/av7330663/）<--既然都用人家代码了我就k一下下

#include<bits/stdc++.h>
#define maxn 200010
using namespace std;
vector<int>E[maxn];
stack<int>S;
int dfn[maxn],low[maxn],tot,n,ans=maxn,vis[maxn];
void tarjan(int x)
{
    low[x]=dfn[x]=++tot;
    S.push(x);vis[x]=1;
    for(int i=0;i<E[x].size();++i)
    {
        int v=E[x][i];
        if(!dfn[v])
        {
            tarjan(v);
            low[x]=min(low[x],low[v]);
        }
        else if(vis[v])
        {
            low[x]=min(low[x],dfn[v]);
        }
    }
    if(low[x]==dfn[x])
    {
        int cnt=0;
        while(1)
        {
            int now=S.top();
            S.pop();
            cnt++;
            if(now==x) break;
        }
        if(cnt>1) ans=min(ans,cnt);
    }
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;++i)
    {
        int x;
        cin>>x;
        E[i].push_back(x);
    }
    for(int i=1;i<=n;++i)
    {
        if(!dfn[i]) tarjan(i);
    }
    cout<<ans<<endl;
    return 0;
}