求逆元的几种方法(点击打开链接)
费马小定理求逆元 a^(p-1) ≡1(mod=p)(p为素数)→a*a^(p-2)≡1(mod=p) 所以a^(p-2)为a的逆元;
求现在来看一个逆元最常见问题,求如下表达式的值(已知 )
)
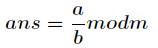
通用的求逆元方法,适合所有情况公式如下(已知 )
)
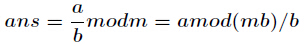
证:

通过扩展欧几里德求逆元时 (前提ab互质)
a*x+b*y=1=gcd(a,b)
b=0时x=1,y=0;
x为a的逆元
证:
∵ax≡1(mod=b)
设ax=b*-y+1;
∴ ax+by=1;
证毕
∵gcd(a,b)=gcd(b,a mod b)
∴a*x1+b*y1=gcd(b,a mod b)
a*x1+b*y1=gcd(b,a-(a/b*b))
设 bx2 + (a%b)y2 = gcd(b, a%b) = gcd(a, b)(!!!因为很多博客都没提到百思不得其解浪费了很久时间 感谢 Jaydenouyang dalao 在博客园的博客)
∴ ax1+by1=bx2+(a mod b)y2
ax1+by1=bx2+(a - (a/b)*b)y2
ax2+by2-(a/b)*b*y2=ax1+by1
横等得:
x1=y2
y1=x2-(a/b)*y2
如此反复递归终有b=0时
最后得出x的解求出逆元

