hdu多校第4场E. Matrix from Arrays HDU 二维前缀和

Problem E. Matrix from Arrays

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 907    Accepted Submission(s): 403


Problem Description
Kazari has an array A length of L, she plans to generate an infinite matrix M using A.
The procedure is given below in C/C++:

int cursor = 0;
for (int i = 0; ; ++i) {
    for (int j = 0; j <= i; ++j) { 
        M[j][i - j] = A[cursor];
        cursor = (cursor + 1) % L;
    }
}


Her friends don't believe that she has the ability to generate such a huge matrix, so they come up with a lot of queries about M, each of which focus the sum over some sub matrix. Kazari hates to spend time on these boring queries. She asks you, an excellent coder, to help her solve these queries.
 

Input
The first line of the input contains an integer T (1≤T≤100) denoting the number of test cases.
Each test case starts with an integer L (1≤L≤10) denoting the length of A.
The second line contains L integers A0,A1,...,AL−1 (1≤Ai≤100).
The third line contains an integer Q (1≤Q≤100) denoting the number of queries.
Each of next Q lines consists of four integers x0,y0,x1,y1 (0≤x0≤x1≤108,0≤y0≤y1≤108) querying the sum over the sub matrix whose upper-leftmost cell is (x0,y0) and lower-rightest cell is (x1,y1).
 

Output
For each test case, print an integer representing the sum over the specific sub matrix for each query.
 

Sample Input
1        
3        
1 10 100
5        
3 3 3 3
2 3 3 3
2 3 5 8
5 1 10 10
9 99 999 1000
 

Sample Output
1
101
1068
2238
33076541
 

Source
2018 Multi-University Training Contest 4
 

Recommend
chendu   |   We have carefully selected several similar problems for you:  6343 6342 6341 6340 6339 
 

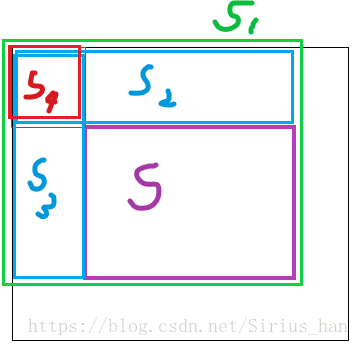
如图二 根据容斥原理S=S1-S2-S3+S4；；S1, S2, S3, S4都是以(x, y)为右下角，以(0, 0)为左上角的矩阵，问题就转化成了求这样的矩阵图一；

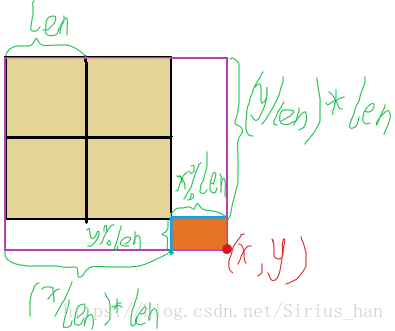
米黄色的面积表示有多少个完整的循环矩阵，下方白条及右方白条表示只有长或宽不完整的矩阵，橙黄色面积表示不完整的循环矩阵；

#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
#define ll long long
ll m[100][100];
ll a[100000];
ll sum[25][25];
ll len;
ll jisuan(int x,int y)
{
    ll ans=(x/len)*(y/len)*sum[len][len];//多少个重复规律
    ans+=sum[x%len][len]*(y/len)+sum[len][y%len]*(x/len);//左边和下面
    ans+=sum[x%len][y%len];//左下角
    return ans;

}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int l;
        scanf("%d",&l);
        for(int i=0;i<l;i++)
            scanf("%lld",&a[i]);
        int cursor = 0;
        for (int i = 0; i<100; ++i)
        {
            for (int j = 0; j <= i; ++j)
            {
                m[j+1][i - j+1] = a[cursor];
                cursor = (cursor + 1) %l;
            }
        }
        len=2*l;
        memset(sum, 0, sizeof(sum));
        for(ll i=1; i<=len; i++){
            for(ll j=1; j<=len; j++){
                sum[i][j]=sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1]+m[i][j];//容斥原理
            }
        }
        int q;
        scanf("%d",&q);
        while(q--)
        {
            int x0,y0,x1,y1;
            scanf("%d%d%d%d",&x0,&y0,&x1,&y1);
            x0++,y0++,x1++,y1++;
            ll ans=0; ans=jisuan(x1,y1)+jisuan(x0-1,y0-1)-jisuan(x0-1,y1)-jisuan(x1,y0-1);
            cout<<ans<<endl;
            
        }
        
    }
    
    return 0;
}