20162327 2017-2018-1 《程序设计与数据结构》第七周学习总结
教材学习内容总结
- 1、树是非线性结构,其元素组织为一个层次结构
- 2、树的度表示树中的任意结点的最大子结点数
- 3、有m个元素的平衡n叉树的高度是lognm
- 4、树的遍历有4种方法
- 5、进行层序遍历时可采用队列来储存树中的元素
- 6、使用数组实现二叉树时,位于位置n的元素的左孩子在(2n+1)的位置,其右孩子在(2*(n+1))的位置
- 7、树的基于数组的存储链实现方式可以占数组中的连续位置,不管树是不是完全树
- 8、如何在一般二叉树中添加及删除元素,要取决于树的用途
- 9、使用决策树可以设计专家系统
- 10、二叉查找树时一颗二叉树,对于其中的每个结点,左子树上的元素小于父结点的值,二右子树上的元素大于等于父结点的值
- 11、如果没有其他的操作,二叉查找树的树形由元素的添加次序来决定
- 12、最有效地二叉查找树时平衡的,所以每次比较时可以排除一半的元素
- 13、当从二叉查找树中删除元素时要考虑三种情形,其中的两种比较简单
- 14、当从二叉查找树中删除有两个子结点的结点时,比较好的办法是用它的中序后继来取代它
- 15、可以对二叉查找树进行旋转以恢复平衡
教材学习中的问题和解决过程
- 问题1:树的遍历
- 问题1解决方案:
1、先序遍历——先访问根,再自左向右遍历子树
2、中序遍历——遍历左子树,然后访问根,然后自左向右遍历余下的各个子树
3、后续遍历——自左向右遍历各个子树,然后访问根
4、层序遍历——从树的顶层(根)打包底层,从左至右,访问树中每层的每个结点
例子:如图所示写出该图的前序、后序、中序、层序遍历顺序 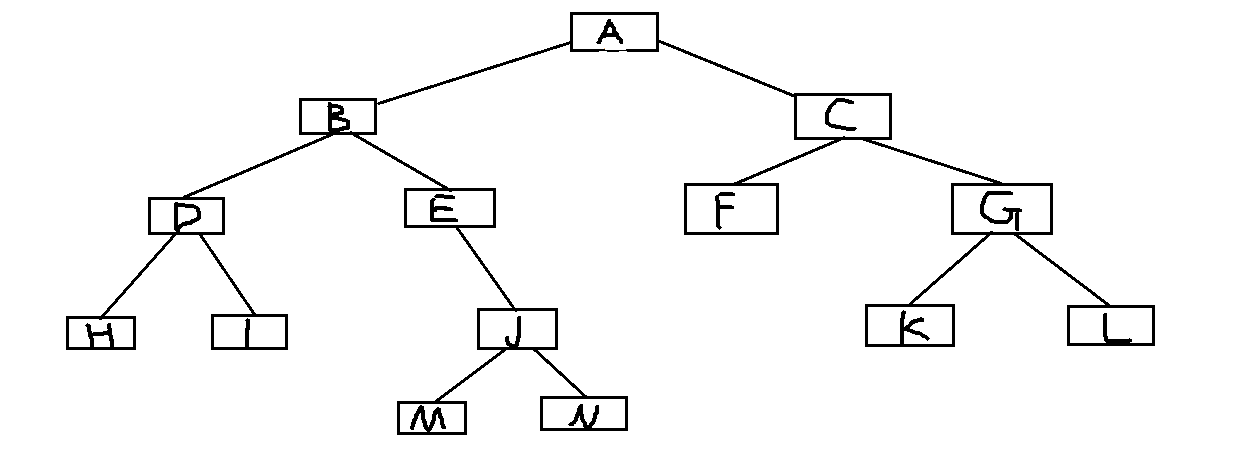
- 先序遍历:ABDHIEJMNCFGKL
中序遍历:HDIBEMJNAFCKGL
后序遍历:HIDMNJEBFKLGCA
层序遍历:ABCDEFGHIJKLMN - 问题2:决策树的有关问题
- 问题2解决方案: 决策树是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。组成包括:决策点,是对几种可能方案的选择,即最后选择的最佳方案。如果决策属于多级决策,则决策树的中间可以有多个决策点,以决策树根部的决策点为最终决策方案。
状态节点,代表备选方案的经济效果(期望值),通过各状态节点的经济效果的对比,按照一定的决策标准就可以选出最佳方案。由状态节点引出的分支称为概率枝,概率枝的数目表示可能出现的自然状态数目每个分枝上要注明该状态出现的概率。
结果节点,将每个方案在各种自然状态下取得的损益值标注于结果节点的右端。
教材中出现的代码问题及解决过程
- 问题一:如何创建一棵树
- 解决方案:
LinkedBinaryTree<String> current = new LinkedBinaryTree<String>("A");//首先创建一个有一个根的树
BTNode<String> a = current.root;//将这个根设置为一个结点,BTNode类会自动产生left和right两个子结点
a.left = new LinkedBinaryTree<String>("B").root;//根据方法 public LinkedBinaryTree (T element, LinkedBinaryTree<T> left,LinkedBinaryTree<T> right)想左右两结点添加元素
a.right = new LinkedBinaryTree<String>("C").root;
(a.left).left = new LinkedBinaryTree<String>("D").root;
(a.left).right = new LinkedBinaryTree<String>("E").root;
(a.right).left = new LinkedBinaryTree<String>("F").root;
(a.right).right = new LinkedBinaryTree<String>("G").root;//构成一个三层的树
问题二:四种遍历方式的代码实现
public Iterator<T> preorder() { //先序遍历
ArrayIterator<T> list = new ArrayIterator<>();
if(root!=null)
root.preorder(list);
return list;
}
public void preorder ( ArrayIterator<T> iter) {
iter.add(element);
if(left!=null)
left.preorder(iter);
if (right != null)
right.preorder(iter);
}
public Iterator<T> postorder() { //后续遍历
ArrayIterator<T> list = new ArrayIterator<>();
if(root!=null)
root.postorder(list);
return list;
}
public void postorder ( ArrayIterator<T> iter) {
if(left != null)
left.postorder(iter);
if(right != null)
right.postorder(iter);
iter.add(element);
}
public Iterator<T> inorder() //中序遍历
{
ArrayIterator<T> iter = new ArrayIterator<T>();
if (root != null)
root.inorder (iter);
return iter;
}public void inorder ( ArrayIterator<T> iter)
{
if (left != null)
left.inorder (iter);
iter.add (element);
if (right != null)
right.inorder (iter);
}
public Iterator<T> levelorder() throws Exception { //层序遍历
LinkedQueue<BTNode<T>> queue = new LinkedQueue<BTNode<T>>();
ArrayIterator<T> iter = new ArrayIterator<T>();
if (root != null)
{
queue.enqueue(root);
while (!queue.isEmpty())
{
BTNode<T> current = queue.dequeue();
iter.add (current.getElement());
if (current.getLeft() != null)
queue.enqueue(current.getLeft());
if (current.getRight() != null)
queue.enqueue(current.getRight());
}
}
return iter;
}
- 前三个方法都是返回一个迭代器,可让用户按所需要的方式扫描树中的每个元素。而层序遍历使用队列来保存元素。
代码托管
本周结对学习情况
其他
- 树的出现让我时一头雾水,可以说树时结合了前几周 学的所有东西,如队列,线表之类的,而树的应用也相当的广泛,例如决策树等等,感觉亚历山大。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 200/200 | 2/2 | 20/20 | |
| 第二周 | 300/500 | 2/4 | 18/38 | |
| 第三周 | 500/1000 | 3/7 | 22/60 | |
| 第四周 | 300/1300 | 2/9 | 30/90 |
参考:软件工程软件的估计为什么这么难,软件工程 估计方法
(有空多看看现代软件工程 课件
软件工程师能力自我评价表)