POJ

题目链接：

http://poj.org/problem?id=1258

题目：

Agri-Net

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 68462		Accepted: 28369

Description

Farmer John has been elected mayor of his town! One of his campaign promises was to bring internet connectivity to all farms in the area. He needs your help, of course. 
Farmer John ordered a high speed connection for his farm and is going to share his connectivity with the other farmers. To minimize cost, he wants to lay the minimum amount of optical fiber to connect his farm to all the other farms. 
Given a list of how much fiber it takes to connect each pair of farms, you must find the minimum amount of fiber needed to connect them all together. Each farm must connect to some other farm such that a packet can flow from any one farm to any other farm. 
The distance between any two farms will not exceed 100,000. 

Input

The input includes several cases. For each case, the first line contains the number of farms, N (3 <= N <= 100). The following lines contain the N x N conectivity matrix, where each element shows the distance from on farm to another. Logically, they are N lines of N space-separated integers. Physically, they are limited in length to 80 characters, so some lines continue onto others. Of course, the diagonal will be 0, since the distance from farm i to itself is not interesting for this problem.

Output

For each case, output a single integer length that is the sum of the minimum length of fiber required to connect the entire set of farms.

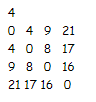
Sample Input

Sample Output

     28

最小生成树prime 模板题

AC代码：

#include <stdio.h>
#include <string.h>
#include <iostream>
using namespace std;
const int inf = 0x3f3f3f3f;
int n,road[105][105],vis[105],minroad,dis[105];

int prime()
{
    memset(vis,0,sizeof(vis));
    for(int i=1; i<=n; i++)
        dis[i]=road[1][i];
    vis[1]=1;
    int sum=0;
    int c=1;
    int i,j;
    while( c < n )
    {
        minroad = inf ;
        for(j=0,i=1; i<=n; i++)
        {
            if(vis[i]==0 && minroad > dis[i])
            {
                minroad = dis[i];
                j=i;
            }
        }
        sum += minroad;
        c++;
        vis[j]=1;
        for(i=1; i<=n; i++)
            if(vis[i]==0 && road[j][i] < dis[i])
                dis[i] = road[j][i];
    }
    return sum;
}

int main()
{
    while(cin>>n)
    {
        if(n==0)break;
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
                cin>>road[i][j];
        printf("%d
",prime());
    }
}