一、矩阵分解
1.案例
我们都熟知在一些软件中常常有评分系统,但并不是所有的用户user人都会对项目item进行评分,因此评分系统所收集到的用户评分信息必然是不完整的矩阵。那如何跟据这个不完整矩阵中已有的评分来预测未知评分呢。使用矩阵分解的思想很好地解决了这一问题。
假如我们现在有一个用户-项目的评分矩阵R(n,m)是n行m列的矩阵,n表示user个数,m行表示item的个数

那么,如何根据目前的矩阵R(5,4)如何对未打分的商品进行评分的预测(如何得到分值为0的用户的打分值)?
——矩阵分解的思想可以解决这个问题,其实这种思想可以看作是有监督的机器学习问题(回归问题)。
矩阵分解的过程中,,矩阵R可以近似表示为矩阵P与矩阵Q的乘积:
矩阵P(n,k)表示n个user和k个特征之间的关系矩阵,这k个特征是一个中间变量,矩阵Q(k,m)的转置是矩阵Q(m,k),矩阵Q(m,k)表示m个item和K个特征之间的关系矩阵,这里的k值是自己控制的,可以使用交叉验证的方法获得最佳的k值。为了得到近似的R(n,m),必须求出矩阵P和Q,如何求它们呢?
2.推导步骤
1.首先令:
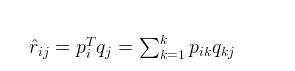
2。对于式子1的左边项,表示的是r^ 第i行,第j列的元素值,对于如何衡量,我们分解的好坏呢,式子2,给出了衡量标准,也就是损失函数,平方项损失,最后的目标,就是每一个元素(非缺失值)的e(i,j)的总和最小值
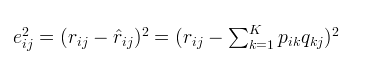
3.使用梯度下降法获得修正的p和q分量:
- 求解损失函数的负梯度
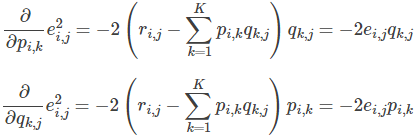
- 根据负梯度的方向更新变量:
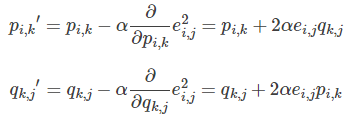
4.不停迭代直到算法最终收敛(直到sum(e^2) <=阈值,即梯度下降结束条件:f(x)的真实值和预测值小于自己设定的阈值)
5.为了防止过拟合,增加正则化项
3.加入正则项的损失函数求解
1.通常在求解的过程中,为了能够有较好的泛化能力,会在损失函数中加入正则项,以对参数进行约束,加入正则L2范数的损失函数为:

对正则化不清楚的,公式可化为:
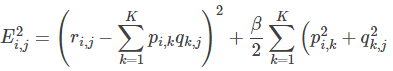
2.使用梯度下降法获得修正的p和q分量:
- 求解损失函数的负梯度:
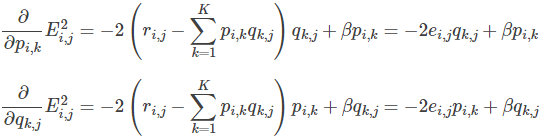
- 根据负梯度的方向更新变量:
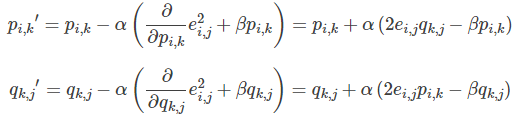
4.预测
预测利用上述的过程,我们可以得到矩阵和,这样便可以为用户 i 对商品 j 进行打分:

二、代码实现
import numpy as np
import matplotlib.pyplot as plt
def matrix(R, P, Q, K, alpha, beta):
result=[]
steps = 1
while 1 :
#使用梯度下降的一步步的更新P,Q矩阵直至得到最终收敛值
steps = steps + 1
eR = np.dot(P,Q)
e=0
for i in range(len(R)):
for j in range(len(R[i])):
if R[i][j]>0:
# .dot(P,Q) 表示矩阵内积,即Pik和Qkj k由1到k的和eij为真实值和预测值的之间的误差,
eij=R[i][j]-np.dot(P[i,:],Q[:,j])
#求误差函数值,我们在下面更新p和q矩阵的时候我们使用的是化简得到的最简式,较为简便,
#但下面我们仍久求误差函数值这里e求的是每次迭代的误差函数值,用于绘制误差函数变化图
e=e+pow(R[i][j] - np.dot(P[i,:],Q[:,j]),2)
for k in range(K):
#在上面的误差函数中加入正则化项防止过拟合
e=e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2))
for k in range(K):
#在更新p,q时我们使用化简得到了最简公式
P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])
Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])
print('迭代轮次:', steps, ' e:', e)
result.append(e)#将每一轮更新的损失函数值添加到数组result末尾
#当损失函数小于一定值时,迭代结束
if eij<0.00001:
break
return P,Q,result
R=[
[5,3,1,1,4],
[4,0,0,1,4],
[1,0,0,5,5],
[1,3,0,5,0],
[0,1,5,4,1],
[1,2,3,5,4]
]
R=np.array(R)
alpha = 0.0001 #学习率
beta = 0.002
N = len(R) #表示行数
M = len(R[0]) #表示列数
K = 3 #3个因子
p = np.random.rand(N, K) #随机生成一个 N行 K列的矩阵
q = np.random.rand(K, M) #随机生成一个 M行 K列的矩阵
P, Q, result=matrix(R, p, q, K, alpha, beta)
print("矩阵Q为:
",Q)
print("矩阵P为:
",P)
print("矩阵R为:
",R)
MF = np.dot(P,Q)
print("预测矩阵:
",MF)
#下面代码可以绘制损失函数的收敛曲线图
n=len(result)
x=range(n)
plt.plot(x, result,color='b',linewidth=3)
plt.xlabel("generation")
plt.ylabel("loss")
plt.show()