实验7:已知某系统在通信联络中只可能出现n种字符,其概率从键盘输入。试创建哈夫曼树。
要求:
1、从键盘输入n, 以及n个字符的概率。
例如:已知某系统在通信联络中只可能出现n种字符,其概率分别为 0.05, 0.29, 0.07, 0.08, 0.14, 0.23, 0.03, 0.11,试设计哈夫曼编码创建哈夫曼树。
2、用顺序存储。
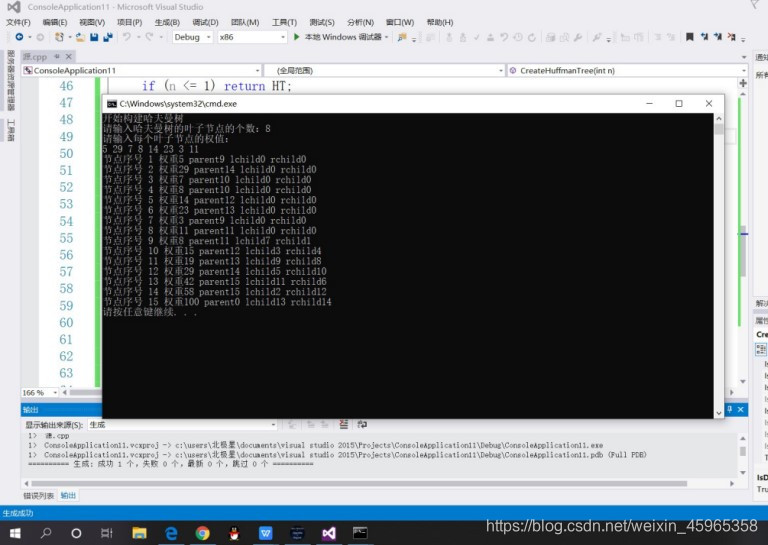
3、输出结果如下

源程序:
#include
#include
using namespace std;
int s1, s2,min1;
typedef struct {
int weight;
int parent, lchild, rchild;
}HTNode, *HuffmanTree;
void Select(HuffmanTree HT, int n)
{
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0)
{
min1 = i;
break;
}
}
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0)
if (HT[i].weight < HT[min1].weight)
min1 = i;
}
s1 = min1;
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0 && i != s1)
{
min1 = i;
break;
}
}
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0 && i != s1)
if (HT[i].weight < HT[min1].weight)
min1 = i;
}
s2 = min1;
}
HuffmanTree CreateHuffmanTree(int n)
{
HuffmanTree HT = NULL;
int i, m;
if (n <= 1) return HT;
m = 2 * n - 1;
HT = new HTNode[m + 1];
for (i = 1; i <= m;i++)
{
HT[i].parent = 0; HT[i].lchild = 0; HT[i].rchild = 0;
}
cout << “请输入每个叶子节点的权值:” << endl;
for (i = 1; i <= n; ++i)
cin >> HT[i].weight;
for (i = n + 1; i <= m; ++i)
{
Select(HT, i - 1);
HT[s1].parent = i; HT[s2].parent = i;
HT[i].lchild = s1; HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight;
}
return (HT);
}
int main()
{
int n, i;
HuffmanTree HT = NULL;
cout << “开始构建哈夫曼树” << endl;
cout << “请输入哈夫曼树的叶子节点的个数:”;
cin >> n;
HT = CreateHuffmanTree(n);
for (i = 1; i <= (2 * n - 1); i++)
{
cout << “节点序号 " << i;
cout<< " 权重” << HT[i].weight;
cout << " parent" << HT[i].parent;
cout << " lchild" << HT[i].lchild;
cout<< " rchild" << HT[i].rchild<<endl;
}
}