Week1绪论--抽象数据类型

一.作业题目

1.构造有理数T，元素e1,e2分别被赋以分子、分母值
2.销毁有理数T
3.用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
4.将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
5.有理数T1,T2相加,结果存入有理数T3
6.有理数T1,T2相减,结果存入有理数T3
7.有理数T1,T2相乘,结果存入有理数T3
8.有理数T1,T2相除,结果存入有理数T3

二.作业内容

1.抽象数据结构描述

ADT Rational{
　　数据结构：
　　　　D={e1,e2,e3,e4|e1,e2为整数}
　　数据关系：
　　　　R={<e1,e2><e3,e4>|e1,e3为有理数的分子，e2,e4为有理数的分母，e2,e4大于0}
　　基本操作：
　　　　InitRational(T1, e1, e2);
　　　　 //操做结果：构造有理数T，元素e1,e2分别被赋以分子、分母值
　　　　DestroyRational( &T);
　　　　 //操做结果：销毁有理数T
　　　　Get(T,i,&e)
　　　　 //操作结果：用e返回有理数T的分子或分母,i为1时返回分子, i为2是返回分母
　　　　Put(&T,i,e)
　　　　 //操作结果：将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
　　　　AddRational(&T1,&T2,&T3)
　　　　 //操作结果：有理数T1,T2相加,结果存入有理数T3
　　　　SubRational(&T1,&T2,&T3)
　　　　 //操作结果：将T1，T2相减，结果存入T3
　　　　MulRational(&T1,&T2,&T3)
　　　　 //操作结果：将T1，T2相乘，结果存入T3
　　　　DivRational(&T1,&T2,&T3)
　　　　 //操作结果：将T1，T2相除，结果存入T3
}ADT Rational

2.数据结构、函数说明

1.头文件

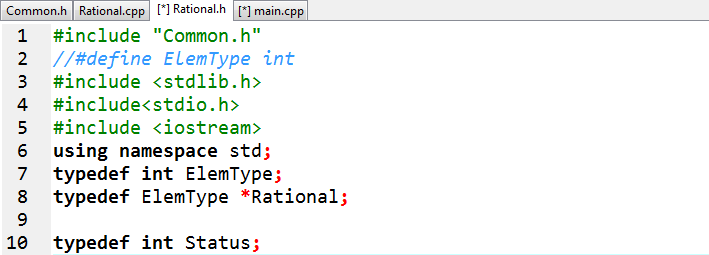
2.函数说明

3.代码实现说明

1.构造有理数

动态申请内存，分别把3个变量放入数组T中

2.销毁有理数

将构造好的有理数从内存中释放

3.用e返回有理数的分子或分母

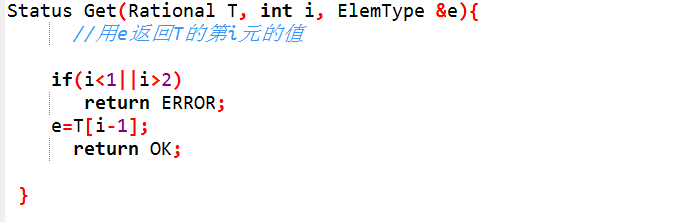
判断输入的i的值，若i=1，返回分子，i=2，返回分母

4.改变有理数的分子或分母为e

判断输入的i的值，若i=1，将e赋值给有理数的分子，i=2，将e赋值给有理数的分母

5.有理数相加

两有理数相加，先通分，相加后，调用最大公约数函数，将所得的有理数化简

6.有理数相减

两有理数相减，先通分，相减后，若相减后所得有理数的分子为0，则有理数为0；若相减后所得有理数的分子不为0，调用最大公约数函数，将所得的有理数化简

7.有理数相乘

两有理数相乘，若分子不为0，则调用最大公约数函数，化简

8.有理数相除

两有理数相除，若分子不为0，则调用最大公约数函数，化简

9.用辗转相除法求最大公约数

若a<b,则将c=a,b=c,a=b, t=a%b,重复循环，保证大数除小数，直到t=0时，这时得到的数即为两有理数的最大公约数

4.结果展示

有理数分母为0或负数

有理数分子为0

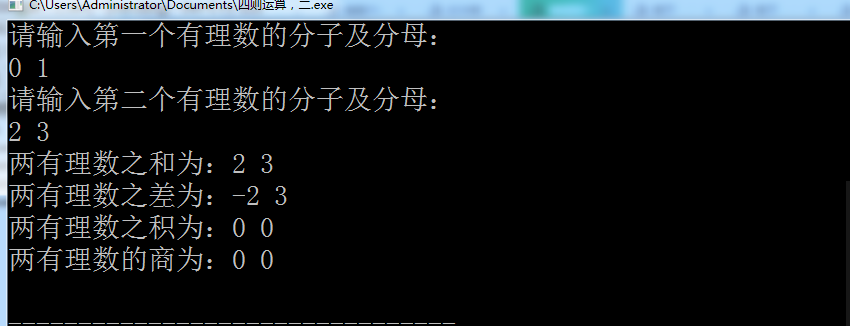
有理数分子为负数

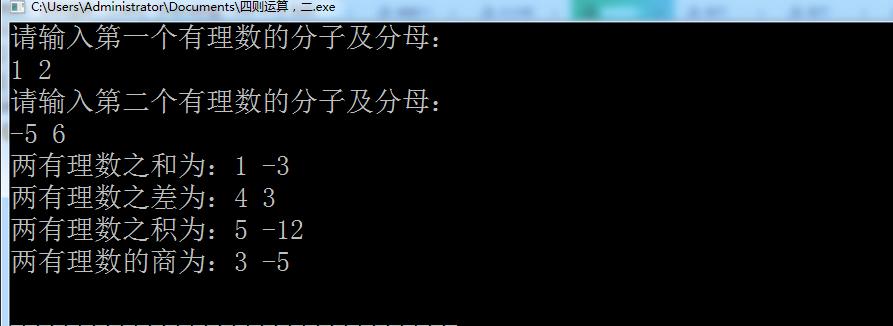
两有理数相等

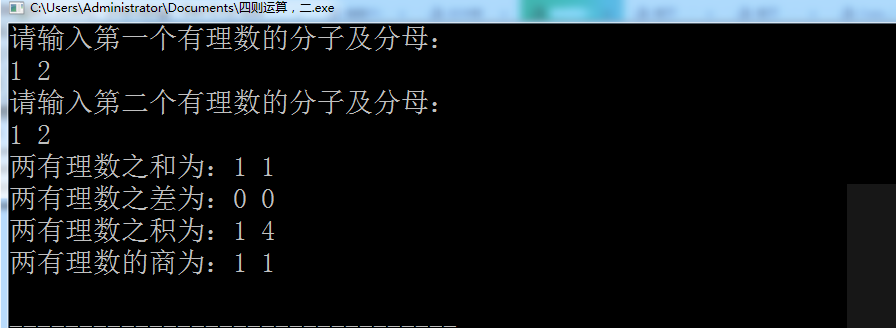
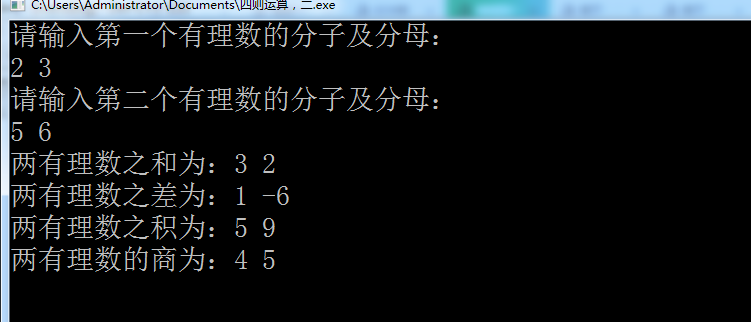
随机有理数

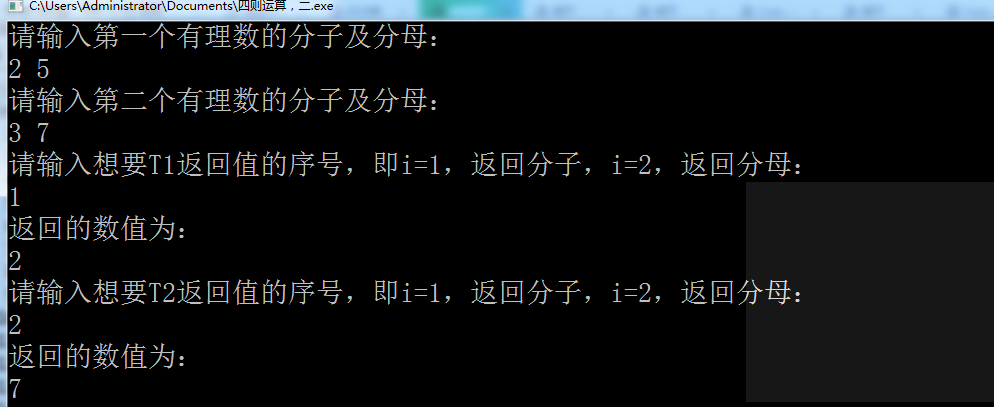
根据i的值返回有理数的分子或分母

6.总结

···

通过这次作业，认识到自己的很多地方的不足，例如&的使用还有还有定义数组和参数传递方面还是需要更深入的去理解，接下来慢慢加强自己的能力吧。

1.数据结构：即是相互间有联系的具有某种组织方式的数据集合。

2.抽象数据类型：即指一个数据模型以及定义在该模型的一组操作，且它的定义取决于它的一组逻辑特性，与其在计算机内部如何表示和实现无关。

···