1.学习总结(2分)
1.1图的思维导图




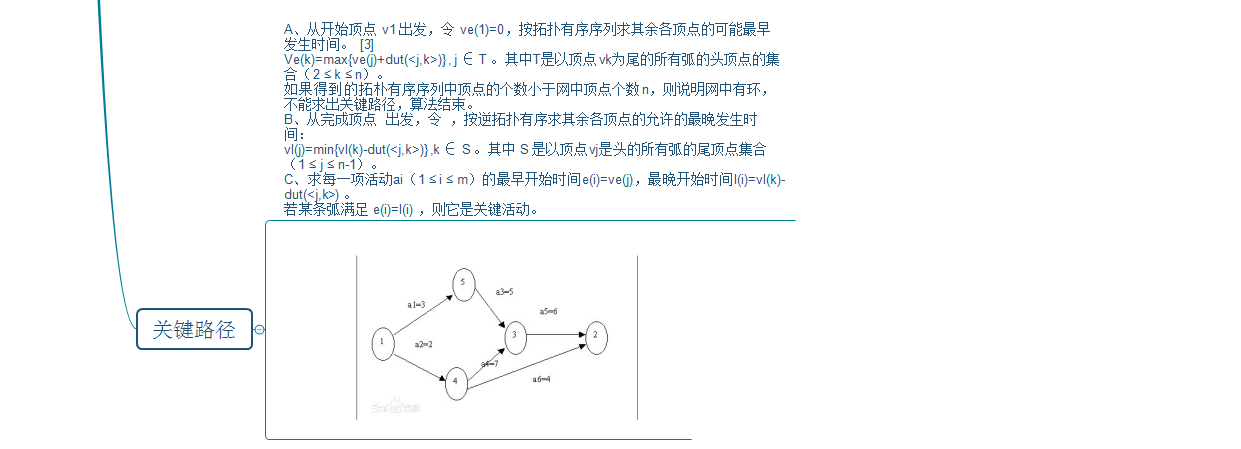
1.2 图结构学习体会
深度遍历的思想:
①访问顶点v;
②依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
③若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
广度遍历的思想:
① 访问顶点vi ;
② 访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ;
③ 依次从这些邻接点(在步骤②中访问的顶点)出发,访问它们的所有未被访问的邻接点; 依此类推,直到图中所有访问过的顶点的邻接点都被访问;
深度优先
数组表示:查找所有顶点的所有邻接点所需时间为O(n2),n为顶点数,算法时间复杂度为O(n2)
广度优先
数组表示:查找每个顶点的邻接点所需时间为O(n2),n为顶点数,算法的时间复杂度为O(n2)
Kruskal VS Prim
方法上:Kruskal在所有边中不断寻找最小的边,Prim在U和V两个集合之间寻找权值最小的连接,共同点是构造过程都不能形成环。
时间上:Prim适合稠密图,复杂度为O(n * n),因此通常使用邻接矩阵储存,复杂度为O(e * loge),而Kruskal多用邻接表,稠密图 Prim > Kruskal,稀疏图 Kruskal > Prim。
空间上: Prim适合点少边多,Kruskal适合边多点少。
Dijkstra算法
算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
拓扑排序算法
执行步骤,由AOV网构造拓扑序列的拓扑排序算法主要是循环执行以下两步,直到不存在入度为0的顶点为止。
(1) 选择一个入度为0的顶点并输出之;
(2) 从网中删除此顶点及所有出边。
循环结束后,若输出的顶点数小于网中的顶点数,则输出“有回路”信息,否则输出的顶点序列就是一种拓扑序列
2.PTA实验作业(4分)
2.1 题目1 7-4 公路村村通(30 分)
2.2 设计思路(伪代码或流程图)
定义数组G存放两条路的预算成本
初始化数组G;
for i=1 to N
输入两条道路编号及预算成本
给G赋初值
定义数组lowcost,closest分别用来标记最近顶点已访问过和最少金额
for i=0 to N
在(V-U)中找出离U最近的顶点k,k记录最近顶点的编号
遍历数组G
如果顶点未被访问过且顶点K到顶点的最少金额小于该顶点的预算成本,则将
lowcost[j]=G[k][j];closest[j]=k;
遍历结束将数组中的最少金额相加
end
2.3 代码截图



2.4 PTA提交列表说明。

本题其主要思路就是求最小生成树的问题,采用prim算法,一开始按照书上的prim算法写的,没有考虑到其边界条件,然后提交果然是边界测试点过不了

后来加了
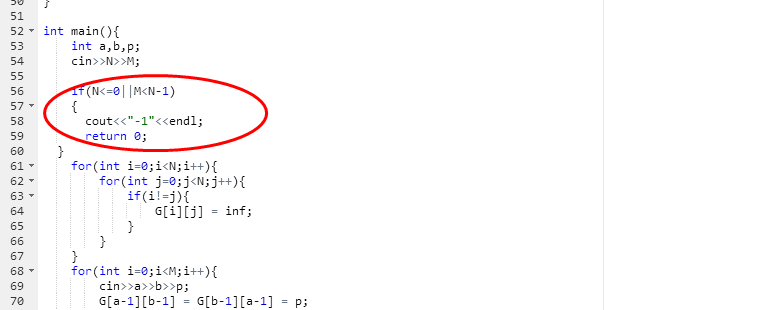
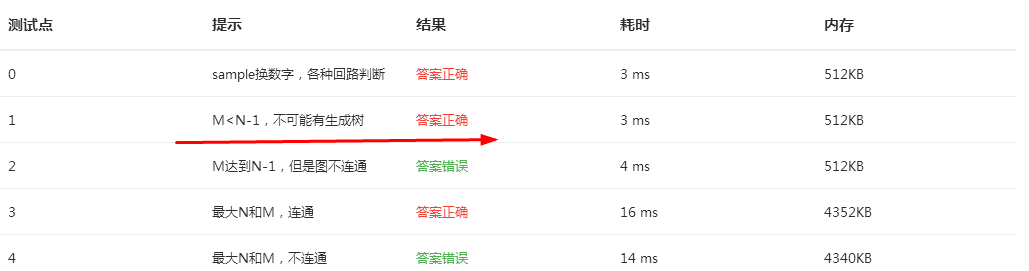
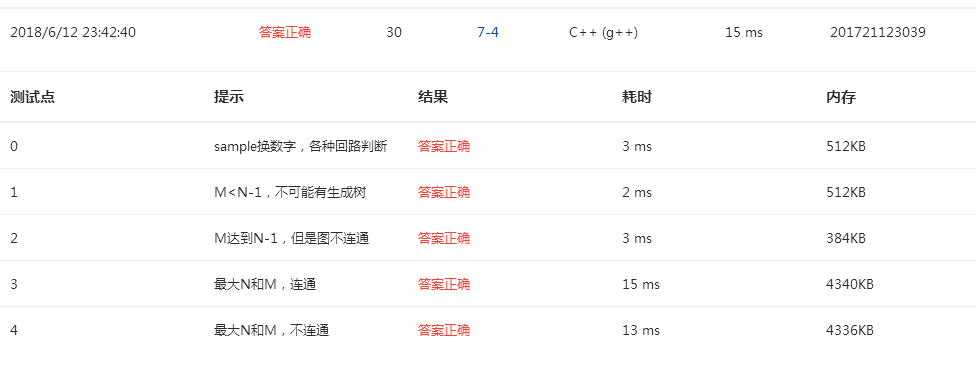
但是还是有两个测试点过不了,后来是最后的金额也需判断

2.1 题目:7-7 旅游规划(25 分)
2.2 设计思路(伪代码或流程图)
定义数组ways[505][505][2];用于储存路径的长度,费用
dist[505],cost[505];分别储存由st出发点到个点的最短路径及其费用
visited[505] = {0};储存个点是否加入集合中
初始化数组ways,dist,cost
for i=0 to M 循环找到最短路径或最少金额
for j=0 to M
找到与初始顶点最近的顶点,用mindis保存该顶点
visited标记该顶点已被访问过
for j=0 to M
如果顶点未被访问过,且到起始顶点的路径大于最短路径
则将最短路径附给dist[j];同时金额也相应改变
如果距离相等则只改变金额
end
2.3 代码截图

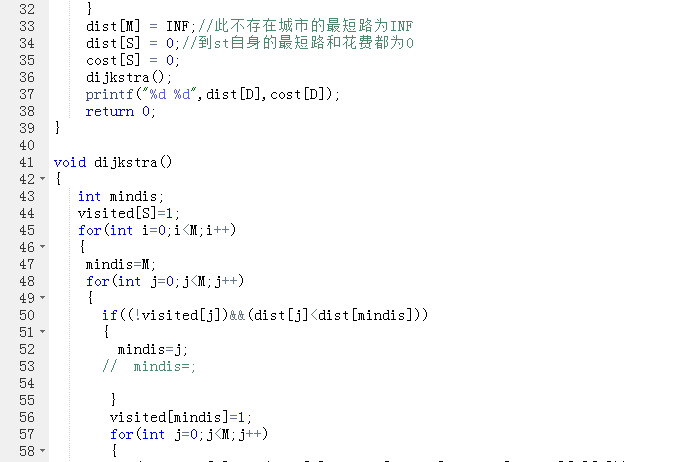

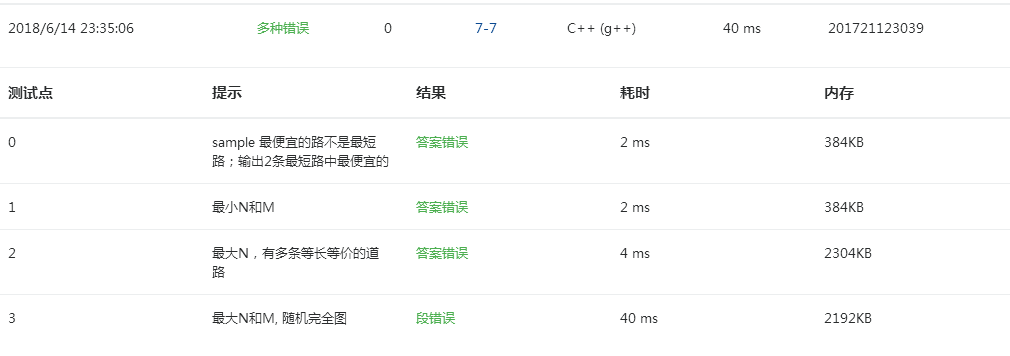
2.4 PTA提交列表说明。

旅游规划这题其主要思路也即最短路径的问题,采用Dijkstra算法,这题没有考虑到其城市是可以从0开始的,还有当最短路径有多条时,需考虑最便宜的路径导致提交时答案错误,
2.1 题目:7-2 排座位(25 分)
2.2 设计思路(伪代码或流程图)
定义数组aor存放两个人的关系
while M--
输入两位宾客以及两人的关系数
用数组aor记录两位宾客的关系
if 宾客关系数为1
则将这两位宾客的编号放入并查集
while K--
输入要查阅的宾客编号m,n
如果aor[m][n]=1,则输出No problem
如果aor[m][n]=-1,
如果在并查集中找到m,n,则输出OK but...
否则输出No way
否则
如果在并查集中找到m,n,则输出No problem
否则输出OK
end
2.3 代码截图



2.4 PTA提交列表说明。

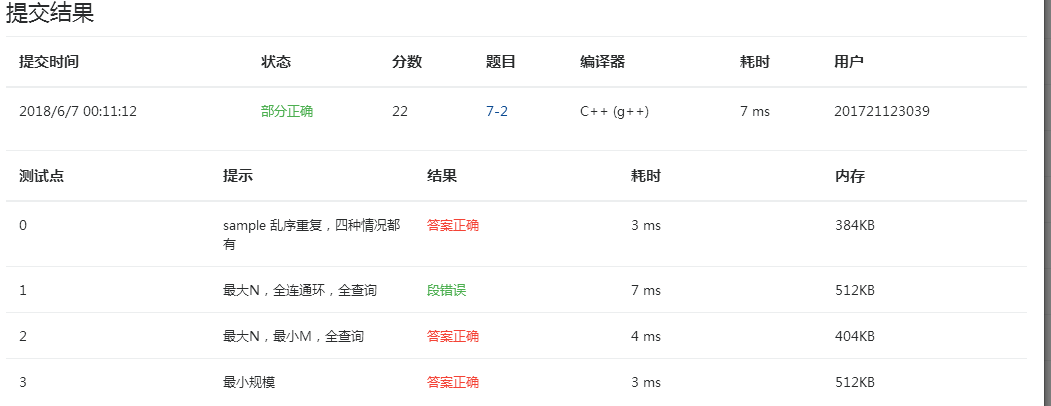
这题一开始是打算用Floyd算法做的,但总是答案错误,后来改用了上一章学习的并查集做的,其解题思路与微信朋友圈的类似,改用并查集后简单多了,但是在写的时候最大值考虑错误
3.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分:195
4. 阅读代码(必做,1分)
代码:7-8 城市间紧急救援(25 分)
思路: 基于dijkstra算法的问题。 要考虑最优路径上的点权和尽可能大,所以出现两路径长度相等时要进行关于点权和的判断。另外还要记录最短路径的条数,只需开一个数组记载,每次更新时基于上一点的最短路径条数更新即可。每次更新最优路径时,将上一点记录在theway数组,用于最后输出最优路径。
代码
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
int N,M,S,D;
int graph[505][505],dis[505],p[505],sum[505],ans[505],theway[505];
// 邻接矩阵 。最短距离 ,每个点的消防队数目, 最多消防队数目, 最短路径条数,经过此点的最优路径的上一个点
bool vis[505]; //记录是否访问此点
void dijkstra()
{
ans[S] = 1;
vis[S] = true;
sum[S] = p[S];
int min_poi;
while(1)
{
min_poi = N;
for(int i = 0 ; i < N; ++i)
{
if( !vis[i] && dis[i] < dis[min_poi])
{
min_poi = i;
}
}
if(min_poi == N) break;
vis[min_poi] = true;
for(int i = 0; i < N; ++i)
{
if(!vis[i])
{
if(dis[i] > dis[min_poi] + graph[min_poi][i])
{
dis[i] = dis[min_poi] + graph[min_poi][i];
ans[i] = ans[min_poi];
sum[i] = sum[min_poi] + p[i];
theway[i] = min_poi;
}
else if(dis[i]==dis[min_poi] + graph[min_poi][i])
{
ans[i] += ans[min_poi];
if( sum[i] < sum[min_poi] + p[i])
{
sum[i] = sum[min_poi] +p[i];
theway[i] = min_poi;
}
}
}
}
}
}
int main()
{
int a,b,c;
scanf("%d%d%d%d",&N,&M,&S,&D);
for(int i = 0; i < N; ++i)
for(int j = 0; j < N; ++j)
graph[i][j] = inf;
for(int i = 0; i < N; ++i )
{
vis[i] = false;
scanf("%d",&p[i]);
}
for(int i = 0; i < M; ++i)
{
scanf("%d%d%d",&a,&b,&c);
graph[a][b] = graph[b][a] = c;
}
for(int i = 0; i < N; ++i)
{
dis[i] = graph[S][i];
if(dis[i] != inf) theway[i] = S;
if(S != i && graph[S][i] != inf)
{
sum[i] = p[i] + p[S];
ans[i] = 1;
}
}
dis[N] = inf;
dijkstra();
printf("%d %d
", ans[D], sum[D]);
int answay[505],rear = 0;
int thepoi = D;
while(1) // 把所求路径上的点储存到数组中,再倒序输出
{
answay[rear++] = theway[thepoi];
thepoi = theway[thepoi];
if(thepoi == S) break;
}
for(int i = (rear - 1); i >= 0; --i)
printf("%d ",answay[i]);
printf("%d",D);
return 0;
}