只是板子和性质, 主要用于复习, 想要学习的话, 去找其他帖子
以前都是懂原理的, 好久不写就忘的差不多了, 这东西会用就好, 懂原理更好
kmp及其扩展
kmp
f[i]表示 模板串t的以第i个字符结尾的后缀字符串 与 模板串前缀字符串 匹配的最大长度
n-f[n] 为字符串的最小循环节长度(忽略最后没显示的) ababa 5-3=2,故循环节(ab)长度为2
aaabaa 最小循环节为aaab,但还有aaaba、aaabaa
对于完美覆盖,最小循环节完美覆盖字符串,则其他循环节必定是最短循环节的倍数
kmp扩展
extend[i]表示 匹配串s的以第i个字符结尾的后缀字符串 与 模板串t前缀字符串 匹配的最大长度
一般用于查找匹配串中有多少个模板串
代码
#include<bits/stdc++.h>
using namespace std;
const int LenT = 1e5 + 5, LenS = 1e6 + 5;
char t[LenT], s[LenS];
int lens, lent;
int f[LenT], extend[LenS];
int cnt;
//n-f[n] 为字符串的最小循环节长度(忽略最后没显示的) ababa 5-3=2,故循环节(ab)长度为2
//aaabaa 最小循环节为aaab,但还有aaaba、aaabaa
//对于完美覆盖,最小循环节完美覆盖字符串,则其他循环节必定是最短循环节的倍数
void KMP()
{
f[1] = 0;
for (int i = 2, j = 0; i <= lent; ++i)
{
while (j > 0 && t[i] != t[j + 1]) j = f[j];
if (t[i] == t[j + 1]) ++j;
f[i] = j;
}
}
void ext_KMP()
{
extend[1] = 0;
for (int i = 1, j = 0; i <= lens; ++i)
{
while (j > 0 && (j == lent || s[i] != t[j + 1]))
j = f[j];
if (s[i] == t[j + 1])
++j;
extend[i] = j;
if (j == lent)
++cnt;
}
}
int main()
{
scanf("%s%s", t+1, s+1);
lens = strlen(s+1);
lent = strlen(t+1);
KMP();
ext_KMP();
printf("%d", cnt);
return 0;
}
Trie数
就是简单的把给的所有串全部放到树中, 但是空间开销较大, 为 (字符种类数^{maxlen}) 或者 maxlen * 字符种类数
通常用于寻找匹配串中有多少模板串
代码
#include<bits/stdc++.h>
using namespace std;
const int SIZE=100+5;
int trie[SIZE][26],tot=1,ended[SIZE];
void insert(char *str)
{
int len=strlen(str),p=1;
for(int k=0;k<len;++k)
{
int ch=str[k]-'a';
if(trie[p][ch]==0)
trie[p][ch]=++tot;
p=trie[p][ch];
}
ended[p]=true;
}
bool search(char *str)
{
int len=strlen(str),p=1;
for(int k=0;k<len;++k)
{
p=trie[p][str[k]-'a'];
if(p==0)
return 0;
}
//如果end[p]=false,则相当于有 cat 查 ca 尽管存在 ca 单词 但并没有 ca
return ended[p];
}
int main()
{
return 0;
}
马拉车
寻找最大回文串
核心思想
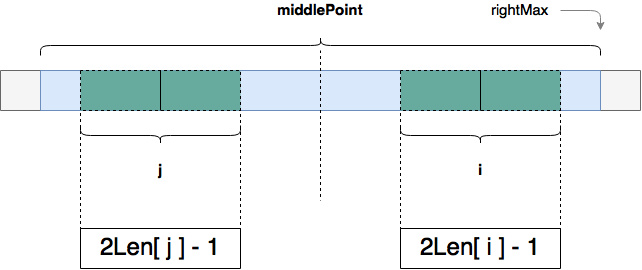
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110005;
int pArr[N << 1];
char s[N], chaArr[N << 1];
int maxLcsplength() {
register int len = 0;
chaArr[len++] = '$', chaArr[len++] = '#';
for (register int i = 0; s[i]; ++i) chaArr[len++] = s[i], chaArr[len++] = '#';
chaArr[len] = '�';
register int R = -1, C = -1, maxN = 0;
for (register int i = 0; i < len; ++i) {
pArr[i] = R > i ? min(R - i, pArr[(C << 1) - i]) : 1;
while (chaArr[i + pArr[i]] == chaArr[i - pArr[i]]) ++pArr[i];
if (i + pArr[i] > R) R = i + pArr[i], C = i;
maxN = max(maxN, pArr[i]);
}
return maxN - 1;
}
int main() {
while (gets(s)) {
printf("%d
", maxLcsplength());
getchar();
}
return 0;
}
字符串环的最大最小表示
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 10000;
char str[N << 1];
int len;
int getMin(char s[]) {
int i = 0, j = 1, k = 0, t;
while (i < len && j < len && k < len) {
t = s[(i + k) % len] - s[(j + k) % len];
if (t == 0) ++k;
else {
if (t > 0) i += k + 1;
else j += k + 1;
if (i == j) ++j;
k = 0;
}
}
return i > j ? j : i;
}
int getMax(char s[]) {
int i = 0, j = 1, k = 0, t;
while (i < len && j < len && k < len) {
t = s[(i + k) % len] - s[(j + k) % len];
if (t == 0) ++k;
else {
if (t < 0) i += k + 1;
else j += k + 1;
if (i == j) ++j;
k = 0;
}
}
return i > j ? j : i;
}
int main()
{
scanf("%s", str + 1);
len = strlen(str + 1);
strncpy(str + len + 1, str + 1, len-1);
char maxa[N], mina[N];
strncpy(maxa + 1, str + getMax(str), len);
strncpy(mina + 1, str + getMin(str), len);
printf("%s
%s", maxa + 1, mina + 1);
return 0;
}
AC自动机
Trie树的思想, 就是多了个失配指针
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#define RE register
#define FOR(i,a,b) for(RE int i=a;i<=b;++i)
#define ROF(i,a,b) for(int i=a;i>=b;--i)
#define ll long long
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%d%d",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define ss(s) scanf("%s",s)
using namespace std;
const int MAXN = 1000005;
const int MAXM = 51;
const int NUM = 10001;
const int C = 'a';
const int M = 26;
struct AC {
static const int N = 1e5 + 5, M = 26, C = 'a'; //字符串总长度, 字符范围
int trie[N][M], cnt[N], fail[N];
vector<VI> idx; //记录节点结尾的字符串id
int q[N], tot;
void init() {
rep (i, 0, M - 1) trie[0][i] = 0;
tot = 0;
idx.resize(1, VI());
}
int newnode() {
cnt[++tot] = 0; fail[tot] = 0;
rep (i, 0, M - 1) trie[tot][i] = 0;
idx.pb(VI());
return tot;
}
void insert(char* s, int id) {
int p = 0;
for (int i = 0; s[i]; ++i) {
int ch = s[i] - C;
if (!trie[p][ch]) trie[p][ch] = newnode();
p = trie[p][ch];
}
++cnt[p];
idx[p].pb(id);
}
void build() {
int head = 0, tail = -1;
rep (i, 0, M - 1) if (trie[0][i]) q[++tail] = trie[0][i];
while (head <= tail) {
int p = q[head++];
rep (i, 0, M - 1)
if (trie[p][i])
fail[trie[p][i]] = trie[fail[p]][i], q[++tail] = trie[p][i];
else trie[p][i] = trie[fail[p]][i];
}
}
int query(char* s) {
set<int> vis;
int p = 0, res = 0;
for (int i = 0; s[i]; ++i) {
p = trie[p][s[i] - C];
for (int tmp = p; tmp && !vis.count(tmp); tmp = fail[tmp])
res += cnt[tmp], vis.insert(tmp);
}
return res;
}
} a;
int _, n;
char s[MAXN];
int main() {
for (sc(_); _; --_) {
sc(n);
FOR(i, 1, n)
ss(s), a.insert(s, i);
a.build();
ss(s);
printf("%d
", a.query(s));
a.init();
}
return 0;
}
后缀数组(nlogn)
太菜了, 只会倍增的写法
sa和rk(rank)数组互逆, sa[i]表示以i为开头的原串的后缀串的排名, rk[i]表示原串后缀串第i名在原串中的位置
后缀数组sa,rk有了没啥用, 主要是得到 heigh数组, hi表示 rk[i] 和 rk[i - 1]的后缀串的最大前缀长度
然后就是倍增rmq
倍增rmq
有的题直接给你一堆字符串, 可以直接sort(), 然后预处理, 按照后缀数组的rmq去写
代码
#include <bits/stdc++.h>
#define RE register
#define FOR(i,a,b) for(RE int i=a;i<=b;++i)
#define ROF(i,a,b) for(RE int i=a;i>=b;--i)
using namespace std;
const int N = 30000 + 9;
char str[N];
int sa[N], rk[N], tp[N], tax[N], lcp[N], len, f[N][30], M;
inline void sort() {
memset(tax, 0, (M + 1) * sizeof(int));
//FOR(i, 0, M)tax[i] = 0;
FOR(i, 1, len) ++tax[rk[i]];
FOR(i, 1, M) tax[i] += tax[i - 1];
ROF(i, len, 1) sa[tax[rk[tp[i]]]--] = tp[i];
}
void getH() {
int j, k = 0;
FOR(i, 1, len) {
if (k) --k;
j = sa[rk[i] - 1];
while (str[i + k] == str[j + k])++k;
lcp[rk[i]] = k;
}
}
void SuffixSort() {
M = 200;
FOR(i, 1, len) rk[i] = str[i], tp[i] = i;
sort();
for (RE int w = 1, p = 0; p < len; w <<= 1, M = p) {
p = 0;
FOR(i, 1, w)tp[++p] = len - w + i;
FOR(i, 1, len)if (sa[i] > w)tp[++p] = sa[i] - w;
sort();
swap(tp, rk);
rk[sa[1]] = p = 1;
FOR(i, 2, len)
rk[sa[i]] = (tp[sa[i - 1]] == tp[sa[i]]
&& tp[sa[i - 1] + w] == tp[sa[i] + w]) ? p : ++p;
}
getH();
}
void rmq_init() {
memset(f, 63, sizeof f);
FOR(i, 0, len-1)f[i][0] = lcp[i + 1];
for (int j = 1,mj=2; mj <= len; ++j,mj<<=1)
for (int i = 1; i + mj <= len; ++i)
f[i][j] = min(f[i][j - 1], f[i + (mj>>1)][j - 1]);
}
int rmq_query(int l, int r) {
if (l<1 || r>len)return 0;
l = rk[l], r = rk[r];
if (l > r)swap(l, r);
int k =r-l<2?0:ceil(log2(r-l))-1;
return min(f[l][k], f[r - (1 << k)][k]);
}
int main() {
scanf("%s", str + 1);
len = strlen(str + 1);
SuffixSort();
getH();
FOR(i, 1, len)
printf("%d ", sa[i]-1);
puts("");
FOR(i,1,len)
printf("%d ",lcp[i]);
return 0;
}
后缀自动机
仿着AC自动机有个失配指针, 不过是endpos等价类的父类
这东西是工具, 要会树上dp才行
//1.如果两个子串�? endpos 相同,则其中子串一个必然为另一个的后缀
//2.对于任意两个子串 t �? p (len_t<=len_p)要么 endpos(p)∈endpos(t) ,要�? endpos(t)∩endpos(p)= �?
//3.对于 endposendpos 相同的子串,我们将它们归为一�? endposendpos 等价类。对于任意一�? endposendpos
//等价类,将包含在其中的所有子串依长度从大到小排序,则每一个子串的长度均为上一个子串的长度�? 11 ,且�?
//上一个子串的后缀(简单来说,一�? endposendpos 等价类内的串的长度连续)
//4.endpos 等价类个数的级别�? O(n)
//5.一个类 aa 中,有最长的子串,也有最短的子串,我们称最长子串的长度�? len(a)len(a) ,最短子�?
//长度�? minlen(a) 。对于存在父子关系的两个类,�? fa(a) 表示�? a 的父亲(也是一个类)。则�? l
//en(fa(a))+1=minlen(a)
//6.后缀自动机的边数�? O(n)O(n)
/////////////////后缀自动机的一般性可以让我们处理的问题有:判断子串,计算不同子串个数等�?
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 4e5 + 10;
struct node
{
int fa, len;
map<char, int> nxt;
}tr[N];
int sz, las;
void init()
{
sz = las = 1;
tr[1].len = tr[1].fa = 0;
map<char, int>().swap(tr[1].nxt);
}
void add(char c)
{
int p = las; int cur = las = ++sz;
tr[cur].len = tr[p].len + 1;
for (; p && !tr[p].nxt.count(c); p = tr[p].fa)
tr[p].nxt[c] = cur;
if (p == 0) { tr[cur].fa = 1; return; }
int q = tr[p].nxt[c];
if (tr[q].len == tr[p].len + 1) { tr[cur].fa = q; return; }
int nq = ++sz; tr[nq] = tr[q];
tr[nq].len = tr[p].len + 1;
for (; p && tr[p].nxt[c] == q; p = tr[p].fa)
tr[p].nxt[c] = nq;
tr[q].fa = tr[cur].fa = nq;
}
int dp[N], n;
char s[N >> 1];
void solve()
{
int lenx = 1, p = 1, tmp = 0;
for(int& i = lenx; s[i]; ++i)
{
if (tr[p].nxt.count(s[i])) p = tr[p].nxt[s[i]], ++tmp;
else
{
while (!tr[p].nxt.count(s[i]) && p) p = tr[p].fa;
if(p == 0) p = 1, tmp = 0;
else tmp = tr[p].len + 1, p = tr[p].nxt[s[i]]; //注意顺序
}
if(!tmp) { puts("-1"); return; }
dp[i] = dp[i - tmp] + 1;
}--lenx;
printf("%d
", dp[lenx]);
}
int main()
{
scanf("%s%d", s + 1, &n); init();
for (int i = 1; s[i]; ++i) add(s[i]);
for (int i = 1; i <= n; ++i)
scanf("%s", s + 1), solve();
return 0;
}