cs231n线性分类器作业 svm代码 softmax

CS231n之线性分类器

斯坦福CS231n项目实战（二）：线性支持向量机SVM

CS231n 2016 通关 第三章-SVM与Softmax

 cs231n：assignment1——Q3: Implement a Softmax classifier

cs231n线性分类器作业：（Assignment 1 ）：

二 训练一个SVM：

steps：

• 完成一个完全向量化的SVM损失函数
• 完成一个用解析法向量化求解梯度的函数
• 再用数值法计算梯度，验证解析法求得结果
• 使用验证集调优学习率与正则化强度
• 用SGD（随机梯度下降）方法进行最优化
• 将最终学习到的权重可视化

1.SVM

支持向量机(Support Vector Machine, SVM)的目标是希望正确类别样本的分数( )比错误类别的分数越大越好。两者之间的最小距离(margin)我们用 来表示，一般令 =1。

对于单个样本，SVM的Loss function可表示为：

将 ， 带入上式：

其中， 表示正确类别， 表示正确类别的分数score， 表示错误类别的分数score。从 表达式来看， 不仅要比 小，而且距离至少是 ，才能保证 。若 ，则 。也就是说SVM希望 与 至少相差一个Δ的距离。

该Loss function我们称之为Hinge Loss

此处使用多分类的hinge loss， Δ=1：　　　

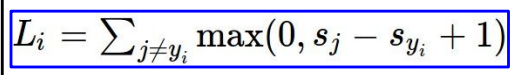
假如一个三分类的输出分数为：[10, 20, -10]，正确的类别是第0类 （yi=0），则该样本的Loss function为：

值得一提的是，还可以对hinge loss进行平方处理，也称为L2-SVM。其Loss function为：

这种平方处理的目的是增大对正类别与负类别之间距离的惩罚。

依照scores带入hinge loss：

依次计算，得到最终值，并求和再平均：

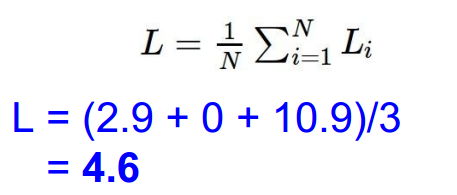
svm 的loss function中bug：

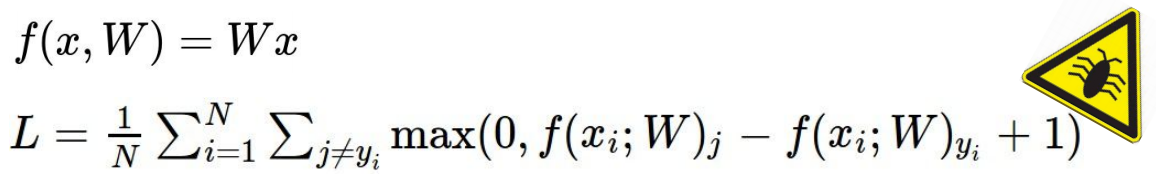
 　　　　简要说明：当loss 为0，则对w进行缩放，结果依旧是0，如何解决？如下图所示：

 

加入正则项：

 

加入正则，对w进行约束，常用的正则有L1 L2

L1趋于选取稀疏的参数，L2趋于选取数值较小且离散的参数。

　　问题1：如果在求loss时，允许j=y_i

　　　　　　此时L会比之前未包含的L大1

　　问题2：如果对1个样本做loss时使用对loss做平均，而不是求和，会怎样？

　　　　　　相当于sum乘以常系数

　　问题4：上述求得的hinge loss的最大值与最小值：

　　　　最小值为0，最大值可以无限大。

　　问题5：通常在初始化f(x,w)中的参数w时，w值范围较小，此时得到的scores接近于0，那么这时候的loss是？

　　　　此时正确score与错误score的差接近于0，对于3classes，loss的结果是2。

2.softmax

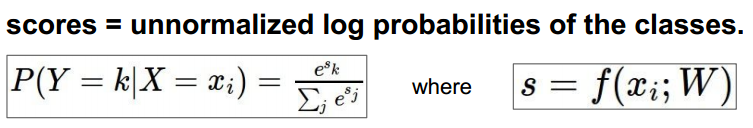
使用似然估计作为loss，本来是似然估计越大越好，但通常loss使用越小时更直观，所以乘以-1：

单一样本：

　　

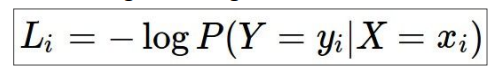
单一样本数值表示：

具体例子：

3、SVM与Softmax比较：

　　模型不同，loss function不同》》

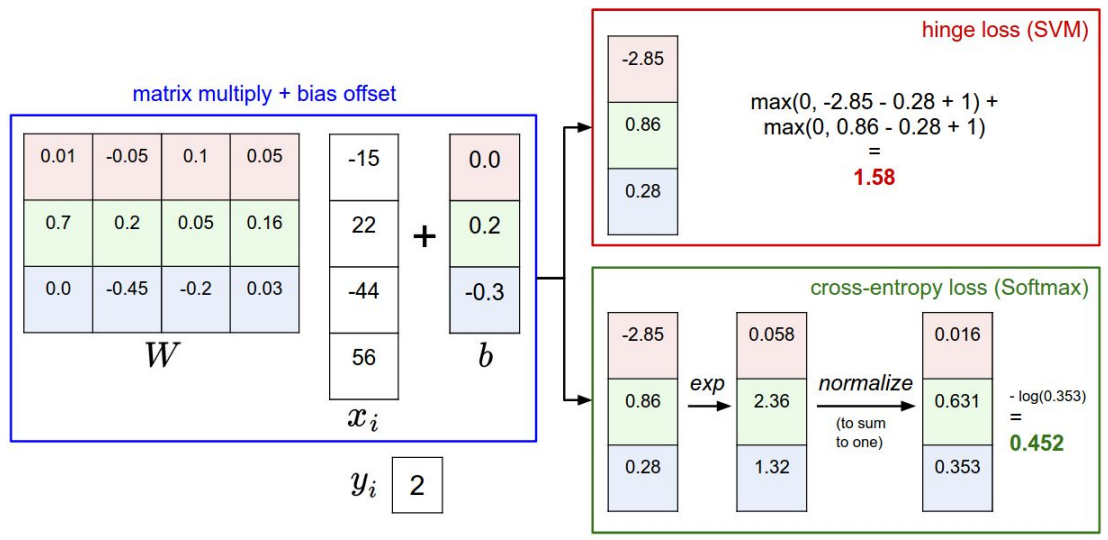
　　loss function：

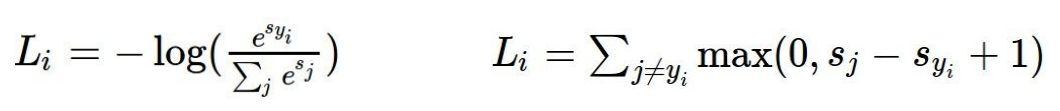
问题8：如果改变对输入数据做改变，即f(x,w)后的值发生变化，此时两个模型的loss分别会怎样变化？（如下例所示）

当改变的值不大时，对svm结果可能没影响，此时改变的点没有超过边界；但当改变较大时，会使得loss变化，此时表示数据点已经跨越了最大边界范围。

但是对softmax而言，无论大小的改变，结果都会相应变化。

4、参数计算

　　对两种模型loss 求和取平均并加入正则项。

方案1：随机选择w，计算得到相应的loss，选取产生的loss较小的w。

方案2：数值计算法梯度下降 

一维求导：

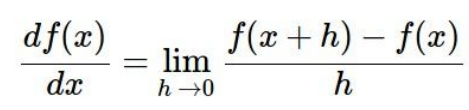
　　多维时，分别对分量求导。具体步骤如下所示： h为定值

　　　　　

　　上述计算了2个分量的偏导。按照此方法求其余分量偏导。代码结构如下图：

　　显然，这种方式计算比较繁琐，参数更新比较慢。

方案三：解析法梯度下降

方案二使用逐一对w进行微量变化，并求导数的方式步骤繁琐，并且产生了很多不必要的步骤。

方案三是直接对w分量求偏导的方式：

 　　　　

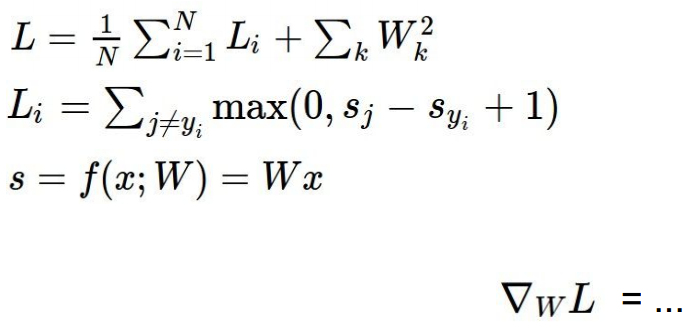
　　对于SVM：

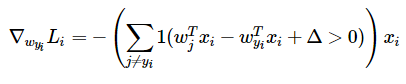
　　对于softmax：

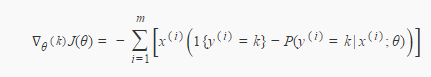
softmax梯度推导

（1）概率

　　（2）似然函数

　　（3）对似然函数关于θq求导

　　　　　　似然函数展开：

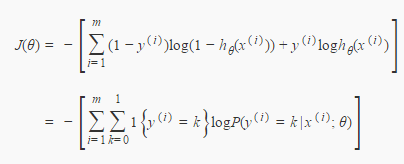
　　　　　　求导：

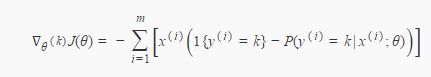
 SVM代码 返回loss和dw 给出两种写法 ：

(1)循环的写法：

def loss_naive(self, X, y, reg):
        """
        Structured SVM loss function, naive implementation (with loops).
        Inputs:
        - X: A numpy array of shape (num_train, D) contain the training data
          consisting of num_train samples each of dimension D
        - y: A numpy array of shape (num_train,) contain the training labels,
          where y[i] is the label of X[i]
        - reg: float, regularization strength
        Return:
        - loss: the loss value between predict value and ground truth
        - dW: gradient of W
        """

        # Initialize loss and dW
        loss = 0.0
        dW = np.zeros(self.W.shape)

        # Compute the loss and dW
        num_train = X.shape[0]
        num_classes = self.W.shape[1] 
        for i in range(num_train):
            scores = np.dot(X[i], self.W)
            for j in range(num_classes):
                if j == y[i]:
                    margin = 0
                else:
                    margin = scores[j] - scores[y[i]] + 1    # delta = 1
                    if margin > 0:
                        loss += margin
                        dW[:,j] += X[i].T
                        dW[:,y[i]] += -X[i].T
        # Divided by num_train
        loss /= num_train
        dW /= num_train

        # Add regularization
        loss += 0.5 * reg * np.sum(self.W * self.W)
        dW += reg * self.W

        return loss, dW

(2)矩阵操作;

def loss_vectorized(self, X, y, reg):
        """
        Structured SVM loss function, naive implementation (with loops).
        Inputs:
        - X: A numpy array of shape (num_train, D) contain the training data
          consisting of num_train samples each of dimension D
        - y: A numpy array of shape (num_train,) contain the training labels,
          where y[i] is the label of X[i]
        - reg: (float) regularization strength
        Outputs:
        - loss: the loss value between predict value and ground truth
        - dW: gradient of W
        """

         # Initialize loss and dW
        loss = 0.0
        dW = np.zeros(self.W.shape)

        # Compute the loss
        num_train = X.shape[0]
        scores = np.dot(X, self.W)
        correct_score = scores[range(num_train), list(y)].reshape(-1, 1)    # delta = -1
        margin = np.maximum(0, scores - correct_score + 1)
        margin[range(num_train), list(y)] = 0
        loss = np.sum(margin) / num_train + 0.5 * reg * np.sum(self.W * self.W)

        # Compute the dW 
        num_classes = self.W.shape[1]
        mask = np.zeros((num_train, num_classes))
        mask[margin > 0] = 1
        mask[range(num_train), list(y)] = 0
        mask[range(num_train), list(y)] = -np.sum(mask, axis=1)
        dW = np.dot(X.T, mask)
        dW = dW / num_train + reg * self.W

        return loss, dW

 dw是Li中j不等于yi时hingeloss大于0的个数的和乘对应的xi的负数，就是下面的式子

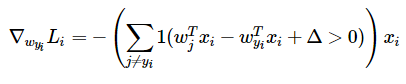
每一列是一个样本经过参数矩阵计算得到的对不同类别的score，Li计算每个样本得分与真实标签的hinge loss

 每个score都是由下面的矩阵计算得到，xi是一个样本，w和b是参数矩阵，f(xi;W,b)是样本对每一类的score：