浅析二分图——最大匹配与最佳匹配
<1> 概念
二分图主要有这几个重要概念:
1.二分图:也就是在一张无向图中,可以把所有定点分成两个子集,且子集内的任意两点都没有边直接相连。二分图的一个等价定义是:不含有「含奇数条边的环」的图。通俗地讲,就是正常性取向,没有男男cp||女女cp
关于二分图的判定——交叉染色法,推荐一个博客:交叉染色法判断二分图
2.匹配:简单来讲,匹配就是「边的集合」,也就是在二分图中找出一些边,使得他们中没有公共点。如图,就是一种匹配。
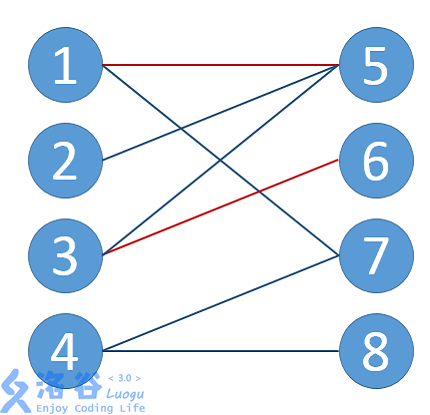
3.最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。如图,即为上一张的最大匹配。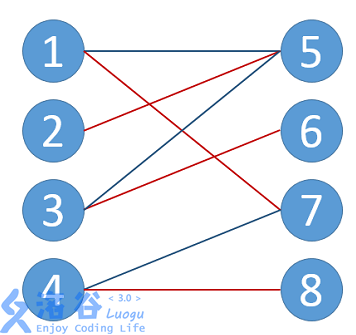
4.最佳匹配:如果在二分图的每一条边上都加上一个权值呢?此时,内个边权和最大的匹配就是最佳匹配。
5.增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。例如,图 5 中的一条增广路如图 6 所示(图中的匹配点均用红色标出):图偷来的
6.交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
<2> 匈牙利算法求最大匹配
由增广路定义可知,增广路有以下特性:(1)增广路的起点和终点必须是非匹配点;(2)增广路中非匹配边比匹配边多1。
由增广路的性质,增广路中的匹配边总是比未匹配边多一条,所以如果我们放弃一条增广路中的匹配边,选取未匹配边作为匹配边,则匹配的数量就会增加。(就是一些博客上的“取反”操作)匈牙利算法就是在不断寻找增广路,如果找不到增广路,就说明达到了最大匹配。
匈牙利算法的核心就是在原始二分图中不停的找增广路,直到找不到为止,或二分图中一边的顶点遍历完。
那么据此可以敲出如下核心代码——寻找增广路
bool findx(int s)
{
for(int i=head[s];i!=-1;i=e[i].nxt)
{
int p=e[i].to;
if(!used[p])
{
used[p]=1;
if(pri[p]==-1||findx(pri[p]))
//若pri[]中的p没有匹配(pri[p]==-1)
//或p已经匹配,但是从中能够找到一条增广路(findx(pri[p]))
{
pri[p]=s;
return 1;
}
}
}
return 0;
}
模板见P3386 【模板】二分图匹配
完整代码:
#include<bits/stdc++.h>
using namespace std;
int e[1005][1005];
int pri[1005];
int used[1005];
int n,m,ans,k;
bool findx(int s)
{
for(int i=1;i<=m;i++)
{
if(!used[i]&&e[s][i]==1)
{
used[i]=1;
if(pri[i]==-1||findx(pri[i]))
{
pri[i]=s;
return 1;
}
}
}
return 0;
}
int main()
{
memset(e,0,sizeof(e));
memset(pri,-1,sizeof(pri));
scanf("%d%d%d",&n,&m,&k);
int x,y;
for(int i=1;i<=k;i++)
{
scanf("%d%d",&x,&y);
e[x][y]=1;
}
ans=0;
for(int i=1;i<=n;i++)
{
memset(used,0,sizeof(used));
if(findx(i)) ans++;
}
printf("%d
",ans);
return 0;
}
<3> KM算法求最佳匹配
这种问题被称为带权二分图的最优匹配问题,可由KM算法解决。
以下借鉴一些BLOG,若有雷同,原作者(dalao)勿喷。
可行顶点标号
用l(v)表示顶点v的标号,w(uv)表示边(u,v)的权,对于赋权二分图G=(X,Y),若对每条边e=xy,均有l(x)+l(y)>=w(xy),则称这个标号为G的一个可行顶点标号。
赋权二分图的可行顶点标号总是存在,一种平凡的可行顶点标号是:l(v)=max w(vy),v∈X y∈Y
l(v)=0,v∈Y
相等子图
设G是一个赋权二分图,l是G的可行顶点标号,边(u,v)上的权为w(uv)。令El={xy∈E(G)|l(x)+l(y)=w(xy)},G中以El为边集的生成子图称为G的l相等子图,记为Gl,注意Gl 的顶点集与G的顶点集相同。
定理
设l是赋权二分图G的一个可行顶点标号,若相等子图有Gl有完美匹配M,则M是G的最大权完美匹配。
Kuhn-Munkras算法(即KM算法)流程:
1.初始化可行顶标的值 (设定lx,ly的初始值)
2.用匈牙利算法寻找相等子图的完备匹配
3.若未找到增广路则修改可行顶标的值
4.重复(2)(3)直到找到相等子图的完备匹配为止
KM算法的核心部分即控制修改可行顶标的策略使得最终可到达一个完美匹配。
1.初始时,设定lx[xi]为和xi相关联的edge(xi,yj)的最大权值,ly[yj]=0,满足公式lx[xi]+ly[yj]>=weight(xi,yj)
2.当相等子图中不包含完备匹配的时候(也就是说还有增广路),就适当修改顶标。直到找到完备匹配为止。(整个过程在匈牙利算法中执行)