经常有一些学弟在QQ或者邮箱上面问我, 机器学习是什么? 我要怎么学习机器学习? 机器学习要如何入门/上手 等类似的问题.
现在我索性就发个博客出来, 以后你们直接来看这个文章就好了~
机器学习是一门研究如何从已有的数据样本中发现该数据样本的数学模型, 而后利用该数学模型对未知数据进行预测的学科.
从学科分类上面来说, 机器学习算是计算统计学与计算机科学的交叉学科. 也因此在不同的大学, 机器学习会隶属于不同的院系. 比如在美国的斯坦福大学,卡内基梅隆大学以及英国的南安普顿大学的计算科学院系都有开始机器学习这门课程(值得一提的是,不同于在其它学校机器学习只是一个专业, 在卡内基梅隆大学机器学习是独立的一个系http://www.ml.cmu.edu/). 而在加州大学伯克利分校的机器学习课程则开设在统计系, 不过该校计算机科学学院也有Practical Machine Learning这门课.
接下来我们谈谈机器学习的应用, 也是为什么近些年机器学习特别火的原因.
机器学习的常见应用包括:
搜索引擎(利用历史点击数据把用户经常点击的结果排在前面)
语音识别技术, 自然语言处理(IBM WATSON, IPHONE 的Siri, 微软的小冰这一类的聊天微软[机器人小冰有什么不一样?])
人脸识别(人脸识别新技术准确率超99%:比肉眼更加精准)
汽车无人驾驶技术(谷歌利用机器学习帮助无人驾驶汽车识别行人)
推荐系统(比如每日头条上面的新闻推荐[今日头条张一鸣:借机器学习给产品带来的价值]
网易云音乐的私人FM, 京东上面的猜你喜欢, QQ聊天窗口上面推荐的广告)
邮件的反垃圾过滤系统(谷歌:人工智能将垃圾邮件拦截率提升至99.9%)
金融机构的风险评估系统,反诈骗系统等(Using machine learning and stream computing to detect financial fraud)
人体基因序列分析, 蛋白质结构预测
日常天气预报以及天文现象预测等, (比如IBM研究院成功将太阳活动和风力预报的精确度提高了30%)
潜在犯罪预测(美国一警局率先利用预测犯罪系统 降低犯罪率)
以及各个行业的专家系统(该挑哪个心理医生?IBM Watson会告诉你)等等.
简单来说机器学习正在成为各行各业都会经常使用到的分析工具.
前文说道, 机器学习研究的是如何从已有的数据样本中发现该数据样本的数学模型, 而后利用该数学模型对未知数据进行预测的学科. 可能有的同学看到这句话时会问什么是数学模型? 什么是未知数据?
数学模型确切来说还没有一个统一的准确的定义, 但是我们可以简单的把数学模型当作是一组方程或者公式. 比如说小学时, 我们学过计算平均速度的数学模型, 中学时学过重力加速度的数学模型. 使用这些数学模型能够帮助我们不必通过实验就可以直接计算(预测)在不同环境(参数)下的物体的平均速度或者瞬时速度
未知数据就是当我们已经有了数据模型时, 如果新的一批数据我们只知道参数而不知道结果的数据(比如 知道了加速度模型, 求铅球在自由落体时, 想求第4秒的瞬时速度, 这个瞬时速度就是一个未知的数据)
别看发现数据样本的数学模型看起来有点不明觉厉的样子, 实际上大家从小学开始就已经学会如何在样本中发现数学模型了! 简单来说就是解方程.
举个一个例子来说:
我们班的同学小谢读三年级时去奶奶家玩, 奶奶家养了好多鸡. 奶奶想考考小谢, 如果三只鸡有6条腿,那么10只鸡会有多少条腿?
小谢当时心想 假设 每只鸡有x条腿 通过创建方程 3 x X = 6 可以算出 x=2. 也就是说鸡脚的数量= 2 x 鸡的数量. 用数学模型来表达就是 Y=2 x X. 所以10只鸡有 Y = 2 x X = 2 x 10 = 20 条腿.
换一个复杂一点的例子:
小谢读六年级时, 在数学课上解过一道数学题.
已知直线经过点A(3,8) B(9,20) 与C点的横坐标x=20, 求C点的纵坐标y
当时小谢写道
解: 由直接方程 a x + b = y 可得方程组
3a +b = 8
9a +b = 20
解方程等 b = 2, a =2 可得该直线为 y = 2x+2 因此当x=20时 y=2*20+2 =42
再来一个再复杂一些的
这是小谢在初中数学课上才学到的!
如下图所示,抛物线y=ax2+bx+c经过点A(-3,0),B(1,0),C(0,-3).求抛物线在D点的坐标!;
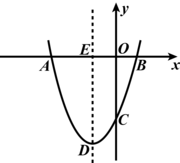
解: 由于抛物线y=ax2+bx+c经过A(-3,0),B(1,0),可设抛物线的解析式为:y=a(x+3)(x-1),将C点坐标(0,-3)代入,得:a(0+3)(0-1)=5,解得a=1,则y=(x+3)(x-1)=x2+2x-3,所以抛物线的解析式为:y=x2+2x-3
当D点横坐标x=-1.5时, D点的纵坐标为 -3.75
好了, 同学们上面的三个例子简单明了的描述了 机器学习最重要的两个步骤:
1. 发现模型(比如通过计算得到Y =2 x X方程式, 通过两个点确定直线方程, 通过三个点确定抛物线方程) ---专业点描述就是 训练的过程
2. 使用模型进行预测(比如 使用方程式计算10只鸡的鸡腿数量, 通过横坐标直接计算直线与抛物线的纵坐标)
好了, 正如大家所感受到的, 机器学习就是一个类似解方程的过程
.
.
.
.
.
.
同学A: 好像都会了耶,
同学B: 不过,.. 好像哪里不对....
同学C: 是了! 我们是怎么知道直线的方程为ax+b=y, 抛物线的方程为y=ax2+bx+c的?
同学D: 额, 万一我们不知道那些个方程怎么办?
(那就且听下回分解吧 ~~)
