DS01-线性表

0.PTA得分截图

1.本周学习内容总结

1.1总结线性表内容

顺序表结构体定义及创建

typedef int ElemType;
typedef struct
{
ElemType data[MaxSize]; //存放顺序表元素
int length:  //存放顺序表的长度
} List;
typedef List* SqList;
void CreateList(SqList &L .int n）//创建顺序表
{
  inti;
  L=new List; 
  L->length=n;
  for(i=0;i<n;i++) cin>>L->data[i];
}

顺序表插入元素e

bool ListInsert(List &L, int i, ElemType e)
{ 
      int j;
      if (i<1 || i>L->length+1)
      return false;  //参数错误时返回false
      i--;//将顺序表逻辑序号转化为物理序号

      for (j=L->length;j>i;j--) //将data[i.. n]元素后移一个位置
      L- >data[j]=L >data[j-1];  
      L->data[i]=e;  //插入元素e
      L->length++;  //顺序表长度增1
      return true;  //成功插入返回true
}

顺序表删除元素e

bool ListDelete(List &L,int i, ElemType &e)

  if (i<1|| i>L->length)//刪除位置不合法
  return false;
  i--; //将顺序表逻辑序号转化为物理序号

  e=L->data[i];
  for (int j=i;j<L->length-1;j++)
  L->data[j]=L->data[j+1];
  L->length--;//顺序表长度减1
  return true;
}

链表的结构体定义

• 链表的节点由数据元素及指针组成，其中数据元素存放数据，指针存放该节点下一个元素的存储位置

typedef struct LNode
{
ElemType   data;//数据域
struct LNode  *next;//指针域
} LNode, *LinkList;

头插法创建单链表

• 具体操作：
  1.声明一个指针变量并初始化空链表L。
  2.让L的头节点的指针指向NULL,即建立一个带头节点的单链表
  3.循环：为新节点nodePtr动态申请内存空间并给其赋值；使新节点指向原来头节点的后面一个节点，头节点指向新节点。

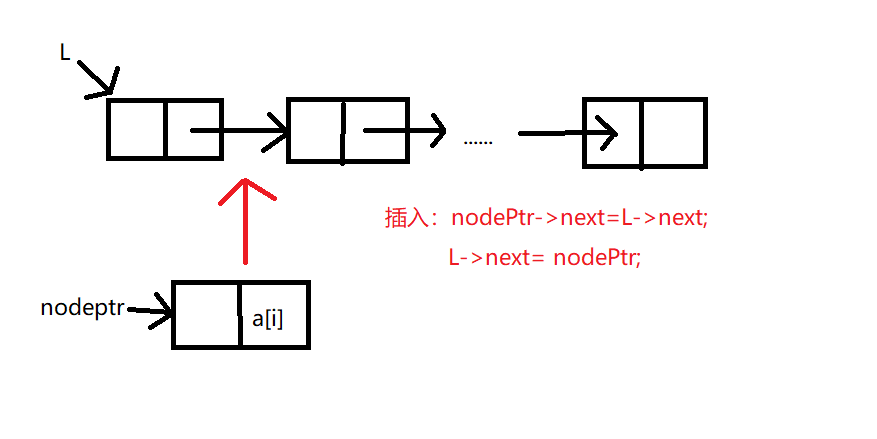
void CreateListF(LinkList &L,ElemType a[],int n)
{
  int i;
  LinkList nodePtr;
  L=new LNode; 
  L->next=NULL;
  
  for(i=0;i<n;i++)
{
  nodePtr=new LNode;
  nodcPtr->data=a[i];
  nodePtr->next=L->next;
  L->next= nodePtr;
}
}

尾插法创建单链表

• 具体操作：
  1.为头节点开辟新空间并使尾指针tailPtr指向头节点L。
  2.生产新节点nodePtr并将数据域赋值想要插入的数据。
  3.将新建的空间地址的指针变量nodePtr的值赋值给尾指针指向的地址，尾指针指向的地址就变成了新插入节点的地址。
  

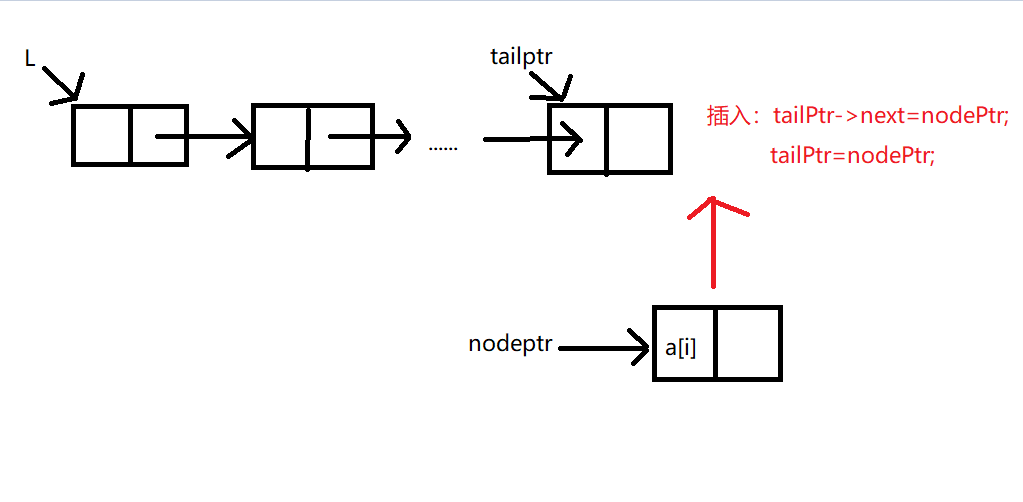
void CreateListR(LinkList &L,ElemType a[],int n)
{
  int i;
  LinkList nodePtr ,ailPtr;
  L=new LNode;
  L->next=NULL;
  tailPtr=L;//尾指针
  for(i=0;i<n;i++)
{
  nodePtr=new LNode;
  nodePtr->data=a[i];
  tailPtr->next=nodePtr;//尾部插入新结点
  tailPtr=nodePtr; 
}
  nodePtr->next=NULL;
}

单链表插入数据元素

bool ListInsert(LinkList &L,int i,ElemType x)//在L中第i个元素之前插入x
{
      int j=0;
      LinkList p=L,s;
      while(p&&j<i-1)
{
      j++;
      p=p->next; 
}
      if(p==NULL) return false;
      s=new LNode;  
      s->data=x;
      s->next=p->next; //插入p后面
      p->next=s;
      return true;
}

单链表删除数据元素

bool ListDelete L(LinkList &L,int i,ElemType &e)
{
  int j=0;
  LinkList p=L,s,q;
  while(p&&j<i-1)
{
  p=p->next;
  j++;
}
  if(p==NULL) return false;
  q=p->next; //第i个位置
  if(q==NULL) return false;
  e=q->data;
  p->next=q->next;//改变指针关系
  delete q;
  return true;
}

有序表插入数据元素

首先构造一个只含头结点和首结点的有序单链表(只含一个数据结点的单链表一定是有序的)。然后扫描单链表L余下的结点(由p指向),在有序单链表中通过比较找插人结点p的前驱结点(由pre指向它),在pre结点之后插人p结点，直到p==NULL为止。

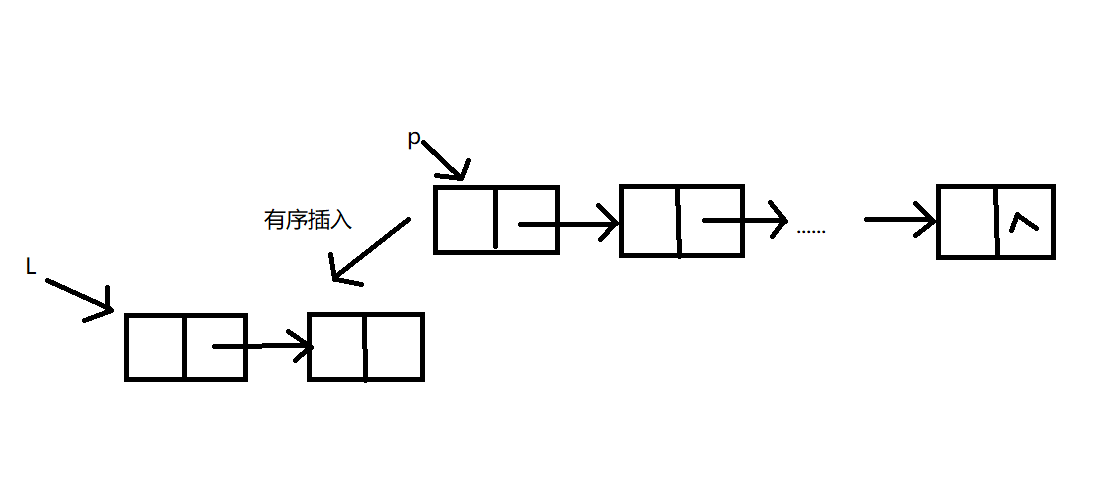
void ListInscrt(LinkNode &L，ElcmType e)
{
  LinkNode pre=L, p;

  while (pre->next!=NULL && pre->next->data<e)
{
  pre=pre->next; //查找插入结点的前驱结点*pre
}
  p=new LinkNode;
  p->data=e;  //创建存放e的数据结点*p
  p->next= pre->next;//在 *pre结点之后插入*p结点
  pre->next =p;
  p=q;
}

有序表的二路归并算法

• 其过程是分别扫描LA和LB两个有序表，当两个有序表都没有扫描完时循环:比较LA、LB的当前元素,将其中较小的元素放人LC中,再从较小元素所在的有序表中取下一个元素。重复这一过程直到LA或LB比较完毕,最后将未比较完的有序表中余下的元素放人LC中。
• 采用顺序表存放有序表时的二路归并算法:

void UnionList(SqList * LA,SqList * LB,SqList * &LC)
{
  int i=0,j=0,k=0;//ij分别为LA、LB的下标,k为LC中元素的个数
  LC= (SqList * )malloc sizeof(SqList));//建立有序顺序表LC
  while (i<LA-> length &.& j< LB - length)
{ 
    if (LA-> data[]<LB-> data[])
  {
    LC-> data[k]= LA-> data[i];
    i++;k++;
  }
    else            //LA-> data[i]> LB-> data[i]
  { 
    LC-> data[k]= LB -> data[i];
    j++;k++;
  }
}
  while (i< LA -> length)//LA 尚未扫描完,将其余元素插人LC中
{
  LC-> data[k]=LA-> data[i];
  i++;k++;
}
  while (j< LB-> length)  //LB 尚未扫描完,将其余元素插人LC中
{
  LC- > data[k]=LB -> data[];
  j++;k++ ;
}
  LC-> length= k;
}

• 采用单链表存放有序表时的二路归并算法:

void UnionListl(LinkNode * LA, LinkNode * LB, LinkNode * &LC)
{
  LinkNode * pa=LA-> next, * pb=LB ->next,*r，*s;
  LC= (LinkNode*)malloc( sizeof( LinkNode));  //创建 LC的头结点
  r=LC;  //r始终指向LC的尾结点
while (pa!= NULL && pb!= NULL)
{
    if (pa-> data<pb > data)
  {
   s= (LinkNode* )malloc sizeof(LinkNode)); //复制 pa所指结点
   s->data= pa -> data;
   r-> next=s;
   r=s;                  //将s结点插人到LC中
   pa= pa -> next;
  }
   else
  {
   s= (LinkNode * )malloc( sizeof(LinkNode)); //复 制pb所指结点
   s-> data=pb -> data;
   r -> next=s;
   r=s;            //将s结点插人到LC中
   pb=pb -> next;
  } 

while (pa!= NULL)
{ 
  s= (LinkNode * )malloc( sizeof(LinkNode);//复制pa所指结点
  s-> data=pa -> data;
  r-> next= s;
  r=s;                  //将s结点插人到LC中
  pa=pa-> next;
}

while (pb!= NULL)
{
  s= (LinkNode * )malloc( sizeof(LinkNode)); //复制pb所指结点
  s-> data=pb -> data;
  r -> next=s;
  r=s;            //将s结点插人到LC中
  pb=pb -> next;
}
r->next= NULL;//尾结点的next城置空
}

双链表的结构体定义

• 在双链表中,由于每个结点既包含一个指向后继结点的指针,又包含一个指向前驱结点的指针，所以当访问过一个结点后既可以依次向后访问每一个结点，也可以依次向前访问每一个结点。因此与单链表相比,双链表中访问一个结点的前、后结点更方便。

typedef struct DNode
{
ElemType data;//存放元素值
struct DNode*prior;//指向前驱结点
struct DNode*next;//指向后继结点
}DLinkNode;//双链表的结点类型

头插法建立双链表

void CreateListF(DLinkNode *&L，ElemTypea[]， int n)//含有n个元素的数组a创建带头结点的双链表L
{ 
  DLinkNode *s; int i;
  L=(DLinkNode *)malloc(sizeof(DLinkNode)); //创建头结点
  L->prior=L->next=NULL; //前后指针域置为NULL
  for (i=0;i<n;i++) //循环建 立数据结点
 { 
  s=(DLinkNode *)malloc(sizeof(DLinkNode));
  s->data=a[i]; //创 建数据结点*s
  s->next=L->next;//将*s插入到头结点之后
  if(L->next!=NULL) //若L存在数据结点， 修改前驱指针
      L->next-> prior=s;
  L->next=s;
  s->prior=L;

 }
}

尾插法建立双链表

void CreateListR(DLinkNode *&L，ElemTypea[], intn)//含有n个元素的数组a创建带头结点的双链表L
{ 
  DLinkNode *s，*r;
  int 1;
  L=(DL inkNode * )malloc(sizeof(DLinkNode)); //创建头结点
  L->prior=L->next=NULL; //前后指针域置为NULL
  r=L; //r始终 指向尾结点，开始时指向头结点
  for (i=0;i<n;i++)  //循环建 立数据结点
  {
    s=(DLinkNode * )malloc(sizeof(DLinkNode));
    s->data=a[i];  //创建数据结点*s
    r->next=s;
    s->prior=r;//将*s插入*r之后
    r=s;//r指向尾结点
  }
  r->next=NULL;//尾结点next域置为NULL
}

循环链表

• 循环链表是另一种形式的链式存储结构，有循环单链表和循环双链表两种类型。它的特点是表中最后一个结点的指针域指向头结点，整个链表形成一个环。它无须增加存储量，仅对表的链接方式稍作改变，即可使得表处理更加方便灵活。
• 在单链表中，从一已知结点出发，只能访问到该结点及其后续结点，无法找到该结点之前的其它结点。而在单循环链表中，从任一结点出发都可访问到表中所有结点。
• 循环链表中没有空指针域，也没有明显的尾端，涉及遍历操作时，其终止条件就不再是像非循环链表那样判别p或p->next是否为空，而是判别它们是否等于某一指定指针，如头指针或尾指针等,例p所指节点为尾节点的条件是：p->next=L。

1.2谈谈你对线性表的认识及学习体会

• 线性表，从名字可以看出来，是具有像线一样的性质的表。它是零个或多个数据元素的有限序列，有顺序存储和链式存储两种形式。也意味着，元素之间是有序的，若元素存在多个，则第一个元素无前驱，最后一个元素无后继，其他每个元素有且只有一个前驱和后继。线性表强调有限，元素个数是有限的。学习线性表，必然要学会各种基本操作，增删查改等，特别是链式表的基本操作，它不像顺序表一样是一片连续的区域，逻辑清晰，它实际操作起来总感觉有点绕，有时候脑子会短路，不明白那行代码的意思。

2.PTA实验作业

2.1.题目1：jmu-ds-区间删除数据

2.1.1代码截图

2.1.2本题PTA提交列表说明

多种错误：两种错误分别是格式错误和答案错误，没有控制好尾部不带空格的问题。
答案错误：调整格式输出，在for循环里面让最后一个数据独立输出不带空格，提交就变成答案错误。
答案错误：后来发现删除后没有修改链表长度，应该加上L->length=j,结果只过了全部删除这一测试点。
部分正确：两次修改提交都是部分正确，没有能删除在区间内的数据，最后不把输出线性表为空和输出数据用if-else语句连起来就对了。

2.2.题目2：jmu-ds-链表倒数第m个数

2.2.1代码截图

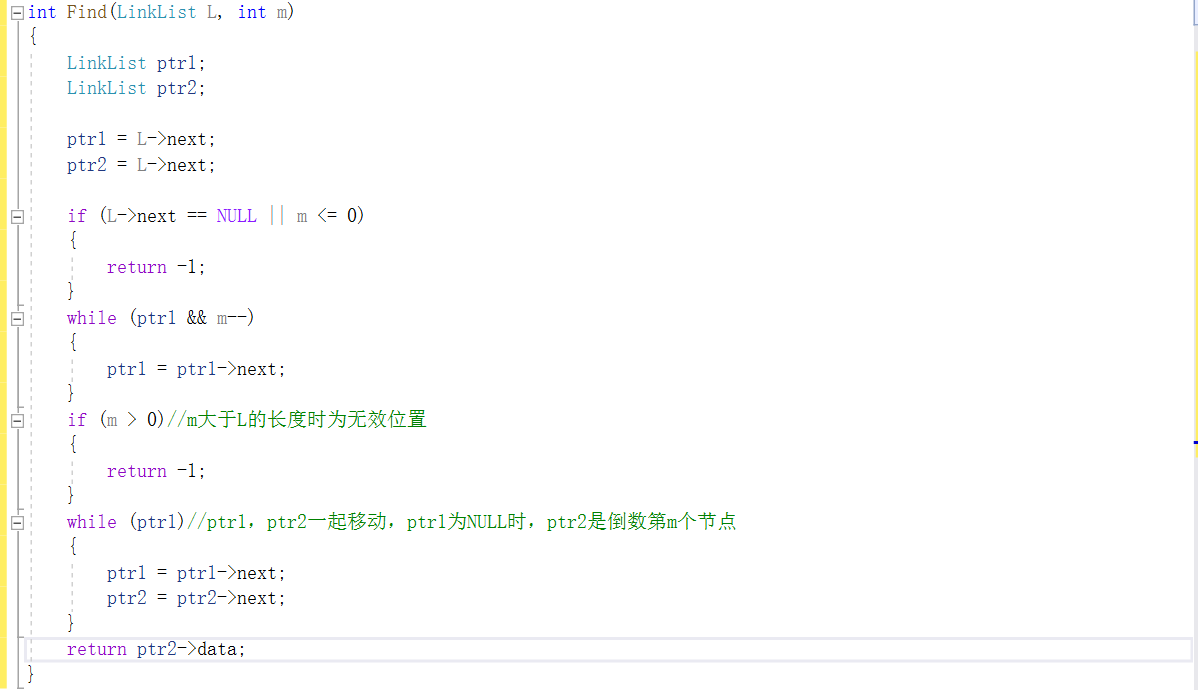
2.2.2本题PTA提交列表说明

段错误：开始没有给两个指针变量初始化，全部测试点都是段错误。
部分正确：加上了ptr1=ptr2=L这条语句，过了两个测试点，测试点2位置无效依然是段错误。
部分正确：改了一下flag,当ptr1为空时将其置为0，则flag==1时两指针一起移动，结果发现后两个测试点过了，但是测试点0却变成答案错误。
部分正确：后来还是改回来，反复修改提交多次总是有测试点过不了。
部分正确：最后将头节点分别指向俩指针，并增加了判断L->next是否为空且m是否是有效位置才完全正确。

2.3.题目3：jmu-ds-有序链表合并

2.3.1代码截图

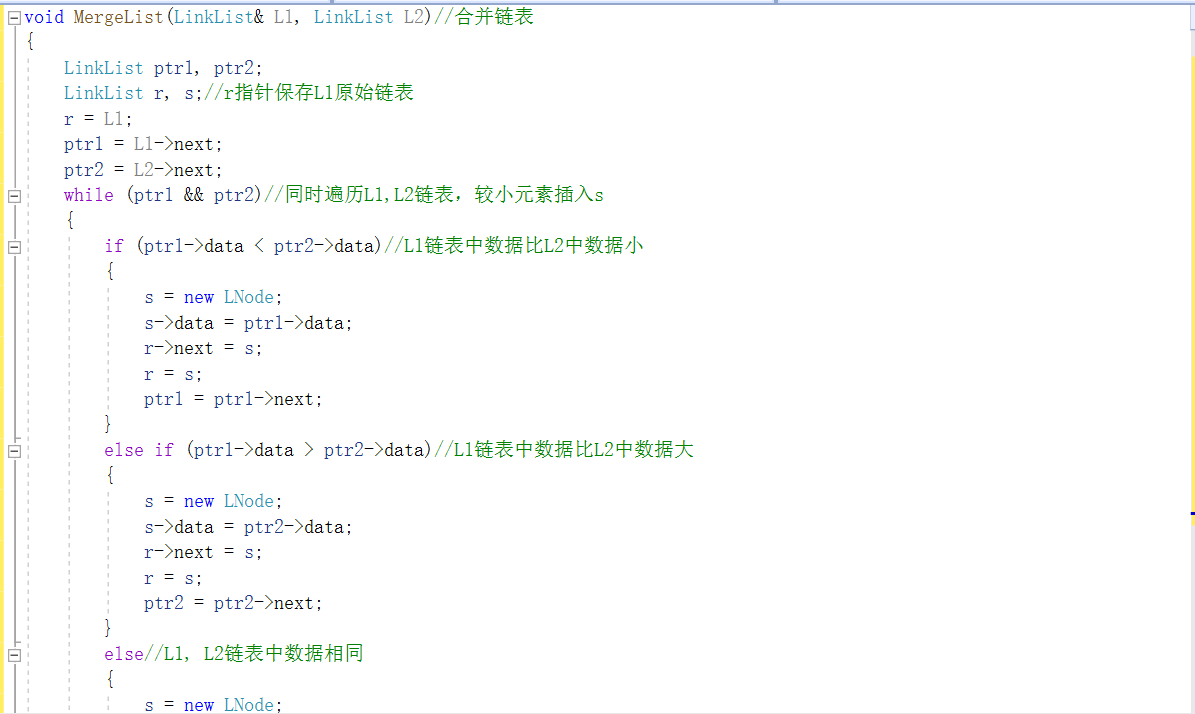
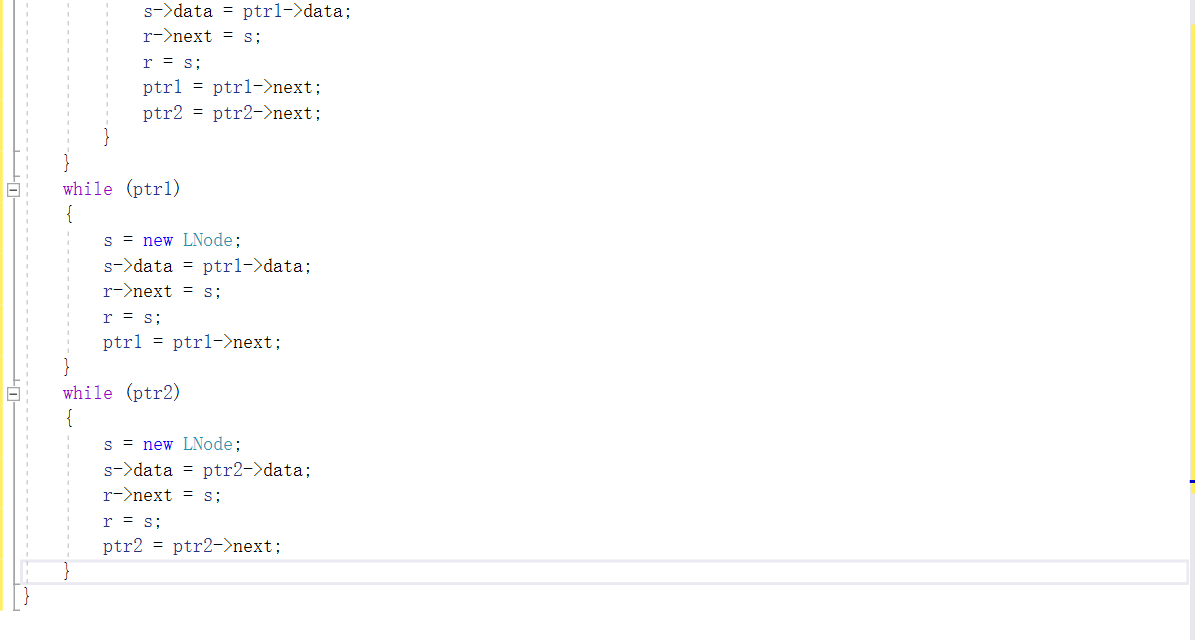
2.3.2本题PTA提交列表说明

部分正确：第一次提交只对了空表的测试点，其他两个测试点提示内存超限。
部分正确：然后发现while循环里面两指针都没有继续移动，分别加上ptr1=ptr1->next和ptr2=ptr2->next,结果内存超限都变成了答案错误。
答案错误：因为插入的时候用了尾插法，于是在最后将尾指针指向空，结果全都错了。
部分正确：前面没有考虑到链表还有剩余数据的情况，所以加上两个while循环判断链表是否有剩余数据，若有则继续插入。

3.阅读代码

3.1 单链表反转 (leetcode 206)

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

struct ListNode* reverseList(struct ListNode* head) {
	struct ListNode* cur = head;
	struct ListNode* prev = NULL;
	while (cur != NULL) {
		struct ListNode* next = cur->next;
		cur->next = prev;
		prev = cur;
		cur = next;
	}
	return prev;
}

3.1.1 该题的设计思路

重新开辟一条链表，然后依次取下原链表的每个结点头插入到新的链表中，新的链表就是逆置的结果。其中时间复杂度为O(n),空间复杂度为O(n)。

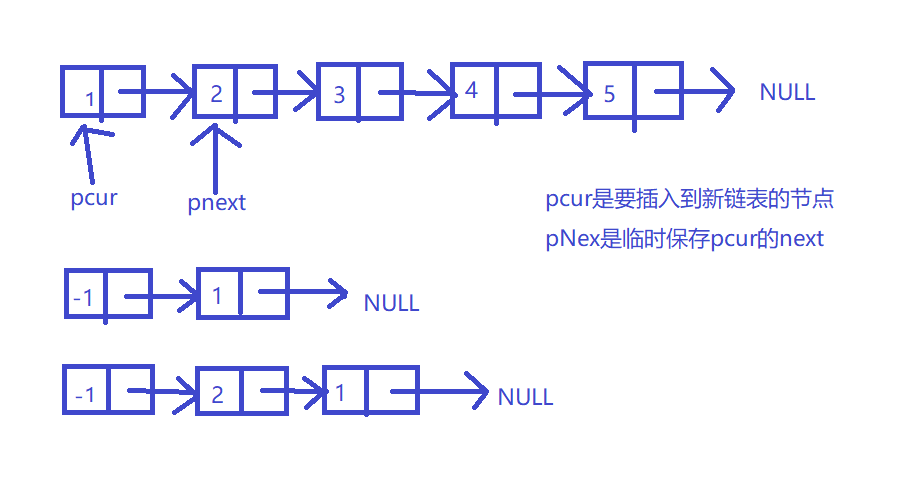
3.1.2 该题的伪代码

定义两个指针，一个指针cur指向链表头结点，另一个指针prev设置为空
while(cur不为空)
{
记录下指针cur后面的结点next;
将指针cur的 next 置为指针prev;
然后更改指针cur为指针next;
指针prev改为指针cur;
}
end while
返回prev的地址;

3.1.3 运行结果

3.1.4分析该题目解题优势及难点

• 代码比较精简，只需要一次遍历，时间复杂度为O(n),巧妙地实现了单链表的逆转。难点是写起来比较绕，不容易理清思路。

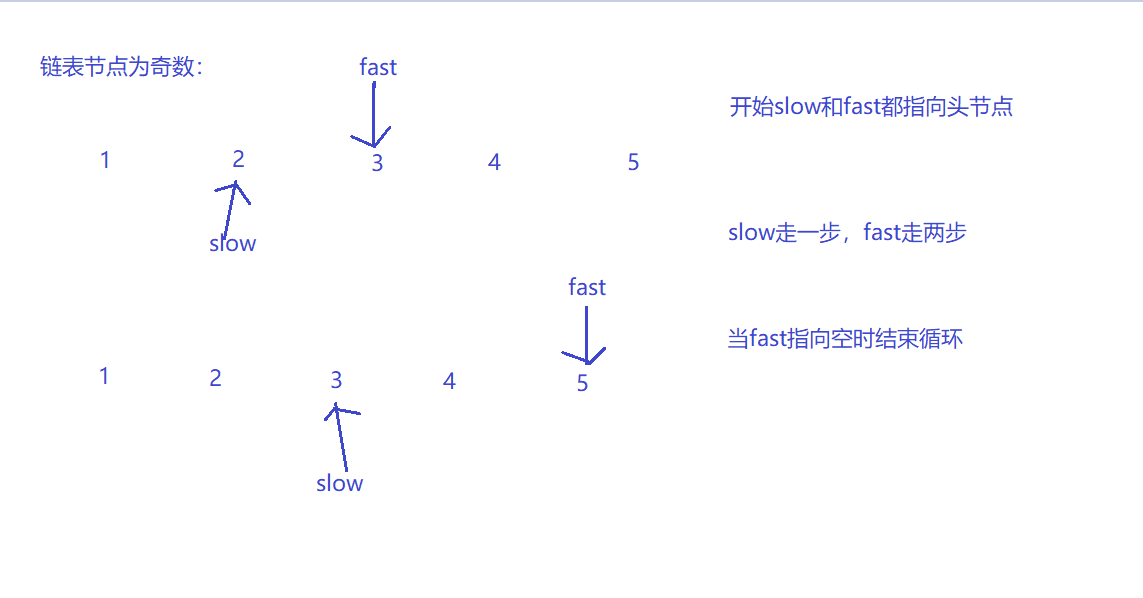
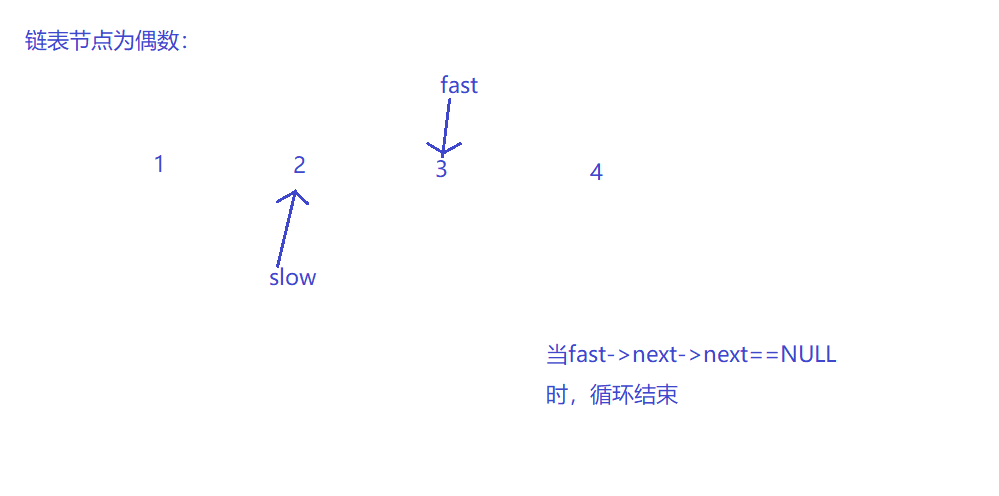
3.2 查找单链表的中间节点

要求只能遍历一次链表,利用快慢指针。

Node* FindMidNode(Node* pHead)  //找单链表的中间节点
{
       Node* slow = pHead, *fast = pHead;
       while (fast && fast->next && fast->next->next) //预防fast为空，奇数时预防fast的next为空，偶数时保证输出前一个元素
       {
              slow = slow->next;  //slow每次走一步，fast每次走两步，当fast到尾时，slow在中间
              fast = fast->next->next;
       }
       return slow;
}

3.2.1 该题的设计思路

思路：慢指针每一次走一步，快指针每次走两步，快指针走到尾或者倒数第二个节点时，慢指针正好走到中间节点。只需要遍历一次而且不用另外开辟新空间，所以其时间复杂度为O(n),空间复杂度为O(1)。

3.2.2 该题的伪代码

定义一个快指针，一个慢指针，它们都指向头节点
while(fast,fast->next和fast->next->next都不为空)
{
  slow指向下一项；
  fast指向下一项的下一项;
}
end slow;
返回slow的地址;

3.2.3 运行结果

3.2.4分析该题目解题优势及难点

• 快慢指针应用非常灵活，代码量少而功能强大，不需要另行开辟新空间。难点是链表的节点可能是奇数也可能是偶数，循环结束的条件不好判断。