紧接上篇~
数据迁移阶段的实现分析
通过分配好迁移的区间之后,开始对数据进行迁移。在看这段代码之前,先来了解一下原理:
synchronized (f)
{//对数组该节点位置加锁,开始处理数组该位置的迁移工作
if (tabAt(tab, i) == f) {//再做一次校验
Node<K, V> ln, hn;//ln 表示低位, hn 表示高位;接下来这段代码的作用是把链表拆分成两部分,0 在低位,1 在高位
if (fh >= 0) {//下面部分代码原理点击这里
int runBit = fh & n;
Node<K, V> lastRun = f;
//遍历当前 bucket 的链表,目的是尽量重用 Node 链表尾部的一部分
for (Node<K, V> p = f.next; p != null; p = p.next) {
int b = p.hash & n;
if (b != runBit) {
runBit = b;
lastRun = p;
}
}
if (runBit == 0) {//如果最后更新的 runBit 是 0,设置低位节点
ln = lastRun;
hn = null;
} else {//否则,设置高位节点
hn = lastRun;
ln = null;
}
//构造高位以及低位的链表
for (Node<K, V> p = f; p != lastRun; p = p.next) {
int ph = p.hash;
K pk = p.key;
V pv = p.val;
if ((ph & n) == 0)
ln = new Node<K, V>(ph, pk, pv, ln);
else
hn = new Node<K, V>(ph, pk, pv, hn);
}
setTabAt(nextTab, i, ln);//将低位的链表放在 i 位置也就是不动
setTabAt(nextTab, i + n, hn);//将高位链表放在 i+n 位置
setTabAt(tab, i, fwd); // 把旧 table 的 hash 桶中放置转发节点,表明此 hash 桶已经被处理
advance = true;
}
//红黑树的扩容部分暂时忽略
}
}
高低位原理分析
ConcurrentHashMap 在做链表迁移时,会用高低位来实现,这里有两个问题要分析一下
1. 如何实现高低位链表的区分
假如我们有这样一个队列

第 14 个槽位插入新节点之后,链表元素个数已经达到了 8,且数组长度为 16,优先通过扩容来缓解链表过长的问题,扩容这块的图解稍后再分析,先分析高低位扩容的原理:
假如当前线程正在处理槽位为 14 的节点,它是一个链表结构,在代码中,首先定义两个变量节点 ln 和 hn,实际就是 lowNode 和 HighNode,分别保存 hash 值的第 x 位为 0 和不等于0 的节点通过 fn&n 可以把这个链表中的元素分为两类,A 类是 hash 值的第 X 位为 0,B 类是 hash 值的第 x 位为不等于 0(至于为什么要这么区分,稍后分析),并且通过 lastRun 记录最后要处理的节点。最终要达到的目的是,A 类的链表保持位置不动,B 类的链表为 14+16(扩容增加的长度)=30,我们把 14 槽位的链表单独伶出来,我们用蓝色表示 fn&n=0 的节点,假如链表的分类是这样:

for(Node<K, V> p = f.next; p !=null;p =p.next)
{
int b = p.hash & n;
if (b != runBit) {
runBit = b;
lastRun = p;
}
}
通过上面这段代码遍历,会记录 runBit 以及 lastRun,按照上面这个结构,那么 runBit 应该是蓝色节点,lastRun 应该是第 6 个节点接着,再通过这段代码进行遍历,生成 ln 链以及 hn 链。
for (Node<K,V> p = f; p != lastRun; p = p.next) {
int ph = p.hash; K pk = p.key; V pv = p.val;
if ((ph & n) == 0)
ln = new Node<K,V>(ph, pk, pv, ln);
else
hn = new Node<K,V>(ph, pk, pv, hn);
}
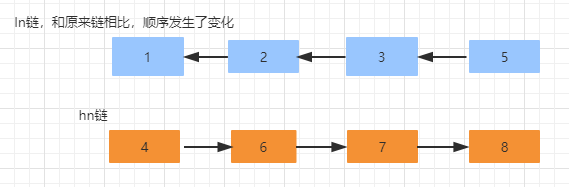
接着,通过 CAS 操作,把 hn 链放在 i+n 也就是 14+16 的位置,ln 链保持原来的位置不动。并且设置当前节点为 fwd,表示已经被当前线程迁移完了 。
setTabAt(nextTab, i, ln);
setTabAt(nextTab, i + n, hn);
setTabAt(tab, i, fwd);
迁移完成以后的数据分布如下

为什么要做高低位的划分
要想了解这么设计的目的,我们需要从 ConcurrentHashMap 的根据下标获取对象的算法来看,在 putVal 方法中 1018 行(f = tabAt(tab, i = (n - 1) & hash)) == null,通过(n-1) & hash 来获得在 table 中的数组下标来获取节点数据,【&运算是二进制运算符,1& 1=1,其他都为 0】,假设我们的 table 长度是 16, 二进制是【0001 0000】,减一以后的二进制是 【0000 1111】,假如某个 key 的 hash 值=9,对应的二进制是【0000 1001】,那么按照(n-1) & hash 的算法,0000 1111 & 0000 1001 =0000 1001 , 运算结果是 9,当我们扩容以后,16 变成了 32,那么(n-1)的二进制是 【0001 1111】,仍然以 hash 值=9 的二进制计算为例,0001 1111 & 0000 1001 =0000 1001 ,运算结果仍然是 9,我们换一个数字,假如某个 key 的 hash 值是 20,对应的二进制是【0001 0100】,仍然按照(n-1) & hash算法,分别在 16 为长度和 32 位长度下的计算结果:
16 位: 0000 1111 & 0001 0100=0000 0100
32 位: 0001 1111 & 0001 0100 =0001 0100
从结果来看,同样一个 hash 值,在扩容前和扩容之后,得到的下标位置是不一样的,这种情况当然是不允许出现的,所以在扩容的时候就需要考虑,而使用高低位的迁移方式,就是解决这个问题.大家可以看到,16 位的结果到 32 位的结果,正好增加了 16:
比如 20 & 15=4 、20 & 31=20 ; 4-20 =16
比如 60 & 15=12 、60 & 31=28; 12-28=16
所以对于高位,直接增加扩容的长度,当下次 hash 获取数组位置的时候,可以直接定位到对应的位置。这个地方又是一个很巧妙的设计,直接通过高低位分类以后,就使得不需要在每次扩容的时候来重新计算 hash,极大提升了效率。
扩容结束以后的退出机制
如果线程扩容结束,那么需要退出,就会执行 transfer 方法的如下代码
//i<0 说明已经遍历完旧的数组,也就是当前线程已经处理完所有负责的 bucket if (i < 0 || i >= n || i + n >= nextn) { int sc; if (finishing) {//如果完成了扩容 nextTable = null;//删除成员变量 table = nextTab;//更新 table 数组 sizeCtl = (n << 1) - (n >>> 1);//更新阈值(32*0.75=24) return; } // sizeCtl 在迁移前会设置为 (rs << RESIZE_STAMP_SHIFT) + 2 // 然后,每增加一个线程参与迁移就会将 sizeCtl 加 1, // 这里使用 CAS 操作对 sizeCtl 的低 16 位进行减 1,代表做完了属于自己的任务 if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) { /*第一个扩容的线程,执行 transfer 方法之前,会设置 sizeCtl = (resizeStamp(n) << RESIZE_STAMP_SHIFT) + 2) 后续帮其扩容的线程,执行 transfer 方法之前,会设置 sizeCtl = sizeCtl+1 每一个退出 transfer 的方法的线程,退出之前,会设置 sizeCtl = sizeCtl-1 那么最后一个线程退出时:必然有sc == (resizeStamp(n) << RESIZE_STAMP_SHIFT) + 2),即 (sc - 2) == resizeStamp(n) << RESIZE_STAMP_SHIFT*/ // 如果 sc - 2 不等于标识符左移 16 位。如果他们相等了,说明没有线程在帮助他们扩容了。也就是说,扩容结束了。 if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT) return; // 如果相等,扩容结束了,更新 finising 变量 finishing = advance = true; // 再次循环检查一下整张表 i = n; // recheck before commit } }
put 方法第三阶段
如果对应的节点存在,判断这个节点的 hash 是不是等于 MOVED(-1),说明当前节点是ForwardingNode 节点,意味着有其他线程正在进行扩容,那么当前现在直接帮助它进行扩容,因此调用 helpTransfer方法 。
else if ((fh = f.hash) == MOVED)
tab = helpTransfer(tab, f);
helpTransfer
从名字上来看,代表当前是去协助扩容
final Node<K, V>[] helpTransfer(Node<K, V>[] tab, Node<K, V> f) {
Node<K, V>[] nextTab;
int sc;
// 判断此时是否仍然在执行扩容,nextTab=null 的时候说明扩容已经结束了
if (tab != null && (f instanceof ForwardingNode) &&
(nextTab = ((ForwardingNode<K, V>) f).nextTable) != null) {
int rs = resizeStamp(tab.length);//生成扩容戳
while (nextTab == nextTable && table == tab && (sc = sizeCtl) < 0) {
//说明扩容还未完成的情况下不断循环来尝试将当前线程加入到扩容操作中
//下面部分的整个代码表示扩容结束,直接退出循环
//transferIndex<=0 表示所有的 Node 都已经分配了线程
//sc=rs+MAX_RESIZERS 表示扩容线程数达到最大扩容线程数
//sc >>> RESIZE_STAMP_SHIFT !=rs, 如果在同一轮扩容中,那么 sc 无符号右移比较高位和 rs 的值,那么应该是相等的。如果不相等,说明扩容结束了
//sc==rs+1 表示扩容结束
if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || transferIndex <= 0)
break;//跳出循环
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) {//在低 16 位上增加扩容线程数
transfer(tab, nextTab);//帮助扩容
break;
}
}
return nextTab;
}
return table;//返回新的数组
}
put 方法第四阶段
这个方法的主要作用是,如果被添加的节点的位置已经存在节点的时候,需要以链表的方式加入到节点中如果当前节点已经是一颗红黑树,那么就会按照红黑树的规则将当前节点加入到红黑树中:
else
{ //进入到这个分支,说明 f 是当前 nodes 数组对应位置节点的头节点,并且不为 空
V oldVal = null;
synchronized (f) { //给对应的头结点加锁
if (tabAt(tab, i) == f) {//再次判断对应下标位置是否为 f 节点
if (fh >= 0) { //头结点的 hash 值大于 0,说明是链表
binCount = 1; //用来记录链表的长度
for (Node<K, V> e = f; ; ++binCount) {//遍历链表
K ek;
//如果发现相同的 key,则判断是否需要进行值的覆盖
if (e.hash == hash &&
((ek = e.key) == key || (ek != null && key.equals(ek)))) {
oldVal = e.val;
if (!onlyIfAbsent) //默认情况下,直接覆盖旧的值
e.val = value;
break;
}
//一直遍历到链表的最末端,直接把新的值加入到链表的最后面
Node<K, V> pred = e;
if ((e = e.next) == null) {
pred.next = new Node<K, V>(hash, key, value, null);
break;
}
}
}//如果当前的 f 节点是一颗红黑树
else if (f instanceof TreeBin) {
Node<K, V> p;
binCount = 2;
//则调用红黑树的插入方法插入新的值
if ((p = ((TreeBin<K, V>) f).putTreeVal(hash, key, value)) != null) {
oldVal = p.val; //同样,如果值已经存在,则直接替换
if (!onlyIfAbsent) p.val = value;
}
}
}
}
判断链表的长度是否已经达到临界值 8. 如果达到了临界值,这个时候会根据当前数组的长度来决定是扩容还是将链表转化为红黑树。也就是说如果当前数组的长度小于 64,就会先扩容。否则,会把当前链表转化为红黑树 :
if (binCount != 0) {//说明上面在做链表操作
//如果链表长度已经达到临界值 8 就需要把链表转换为树结构
if (binCount >= TREEIFY_THRESHOLD)
treeifyBin(tab, i);
if (oldVal != null)//如果 val 是被替换的,则返回替换之前的值
return oldVal;
break;
}
treeifyBin
在 putVal 的最后部分,有一个判断,如果链表长度大于 8,那么就会触发扩容或者红黑树的转化操作。
private final void treeifyBin(Node<K, V>[] tab, int index) {
Node<K, V> b;
int n, sc;
if (tab != null) {
if ((n = tab.length) < MIN_TREEIFY_CAPACITY) //tab 的长度是不是小于 64, 如果是,则执行扩容
tryPresize(n << 1);
else if ((b = tabAt(tab, index)) != null && b.hash >= 0) {//否则,将当前链表转化为红黑树结构存储
synchronized (b) {// 将链表转换成红黑树
if (tabAt(tab, index) == b) {
TreeNode<K, V> hd = null, tl = null;
for (Node<K, V> e = b; e != null; e = e.next) {
TreeNode<K, V> p = new TreeNode<K, V>(e.hash, e.key, e.val, null, null);
if ((p.prev = tl) == null)
hd = p;
else
tl.next = p;
tl = p;
}
setTabAt(tab, index, new TreeBin<K, V>(hd));
}
}
}
}
}
tryPresize
tryPresize 里面部分代码和 addCount 的部分代码类似,看起来会稍微简单一些:
private final void tryPresize(int size) {
//对 size 进行修复 ,主要目的是防止传入的值不是一个 2 次幂的整数 ,然 后通过tableSizeFor 来讲入参转化为离该整数最近的 2 次幂
int c = (size >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY :
tableSizeFor(size + (size >>> 1) + 1);
int sc;
while ((sc = sizeCtl) >= 0) {
Node<K, V>[] tab = table;
int n;
//下面这段代码和 initTable 是一样的,如果 table 没有初始化,则开始初始化
if (tab == null || (n = tab.length) == 0) {
n = (sc > c) ? sc : c;
if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) {
try {
if (table == tab) {
@SuppressWarnings("unchecked")
Node<K, V>[] nt = (Node<K, V>[]) new Node<?, ?>[n];
table = nt;
sc = n - (n >>> 2);//0.75
}
} finally {
sizeCtl = sc;
}
}
} else if (c <= sc || n >= MAXIMUM_CAPACITY)
break;
else if (tab == table) {//这段代码和 addCount 后部分代码是一样的,做辅助扩容操作
int rs = resizeStamp(n);
if (sc < 0) {
Node<K, V>[] nt;
if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || (nt = nextTable) == null || transferIndex <= 0)
break;
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1))
transfer(tab, nt);
} else if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2))
transfer(tab, null);
}
}
}
至此,ConcurrentHashMap的源码全部分析完毕,篇幅太长,有兴趣的朋友可以选择性阅读~