PTA数据结构与算法题目集(中文) 7-33
7-33 地下迷宫探索 (30 分)
地道战是在抗日战争时期,在华北平原上抗日军民利用地道打击日本侵略者的作战方式。地道网是房连房、街连街、村连村的地下工事,如下图所示。
我们在回顾前辈们艰苦卓绝的战争生活的同时,真心钦佩他们的聪明才智。在现在和平发展的年代,对多数人来说,探索地下通道或许只是一种娱乐或者益智的游戏。本实验案例以探索地下通道迷宫作为内容。
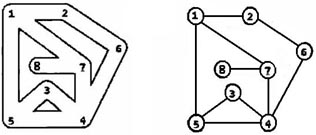
假设有一个地下通道迷宫,它的通道都是直的,而通道所有交叉点(包括通道的端点)上都有一盏灯和一个开关。请问你如何从某个起点开始在迷宫中点亮所有的灯并回到起点?
输入格式:
输入第一行给出三个正整数,分别表示地下迷宫的节点数N(1,表示通道所有交叉点和端点)、边数M(≤,表示通道数)和探索起始节点编号S(节点从1到N编号)。随后的M行对应M条边(通道),每行给出一对正整数,分别是该条边直接连通的两个节点的编号。
输出格式:
若可以点亮所有节点的灯,则输出从S开始并以S结束的包含所有节点的序列,序列中相邻的节点一定有边(通道);否则虽然不能点亮所有节点的灯,但还是输出点亮部分灯的节点序列,最后输出0,此时表示迷宫不是连通图。
由于深度优先遍历的节点序列是不唯一的,为了使得输出具有唯一的结果,我们约定以节点小编号优先的次序访问(点灯)。在点亮所有可以点亮的灯后,以原路返回的方式回到起点。
输入样例1:
6 8 1
1 2
2 3
3 4
4 5
5 6
6 4
3 6
1 5
输出样例1:
1 2 3 4 5 6 5 4 3 2 1
输入样例2:
6 6 6
1 2
1 3
2 3
5 4
6 5
6 4
输出样例2:
6 4 5 4 6 0
题目分析:一道利用图的深度优先遍历的题
收获:认识到了自己对数据结构的应用还不够熟练 别人用20行左右代码就写完这个了 
1 #define _CRT_SECURE_NO_WARNINGS 2 #include<stdio.h> 3 #include<string.h> 4 #include<malloc.h> 5 6 typedef struct ENode* Edge; 7 struct ENode 8 { 9 int V1, V2; 10 }; 11 12 typedef struct GNode* Graph; 13 struct GNode 14 { 15 int G[1010][1010]; 16 int Nv; 17 int Ne; 18 }; 19 20 int IsEdge(Graph Gra,int V1, int V2) 21 { 22 return Gra->G[V1][V2]; 23 } 24 25 void Insert(Graph Gra, Edge E) 26 { 27 Gra->G[E->V1][E->V2] = 1; 28 Gra->G[E->V2][E->V1] = 1; 29 } 30 31 Graph CreateGraph(int Nv) 32 { 33 Graph Gra = (Graph)malloc(sizeof(struct GNode)); 34 Gra->Nv = Nv; 35 Gra->Ne = 0; 36 for (int i = 1; i <= Gra->Nv; i++) 37 for (int j = 1; j <= Gra->Nv; j++) 38 Gra->G[i][j] = 0; 39 return Gra; 40 } 41 42 int Collected[1010]; 43 int cnt=1; 44 int F; 45 void DFS(Graph Gra, int V) 46 { 47 if (F)printf(" "); 48 F++; 49 printf("%d", V); 50 for (int i = 1; i <= Gra->Nv;i++) 51 { 52 if (!Collected[i] && IsEdge(Gra, V, i)) 53 { 54 cnt++; 55 Collected[i] = 1; 56 DFS(Gra, i); 57 printf(" %d", V); 58 } 59 } 60 } 61 62 int main() 63 { 64 int N, M, V; 65 Edge E = (Edge)malloc(sizeof(struct ENode)); 66 scanf("%d%d%d", &N, &M, &V); 67 Graph Gra = CreateGraph(N); 68 Gra->Ne = M; 69 for (int i = 0; i < Gra->Ne; i++) 70 { 71 scanf("%d%d", &(E->V1), &(E->V2)); 72 Insert(Gra, E); 73 } 74 Collected[V] = 1; 75 DFS(Gra, V); 76 if (cnt != Gra->Nv) 77 printf(" 0"); 78 return 0; 79 80 }