真就全网最详基础线段树

最初等版本的线段树

你以为我是树状数组?
其实我是线段树哒!

这两个东西作为同是数据结构又同是树状的东西,很让人迷糊,
你看ta们的题号:


然而看代码长度就容易区分多了

那么ta们之间到底有什么联系(废话,都是树状呗)与不同呢(名称)
先讲完线段树再归纳整理吧
线段树可维护的东西可比上面的辣鸡ST和树状数组多(好像后面就不用归纳整理了...)

关于长相大致形态

ta是这样一种结构:

当然这是将区间以数字形式表现,也可以直观表现,像这样:

(p.s. 这里的"ROOT"点并不是将最顶上的线段一分为二,最上面的线段就是一条线段,也就是说这个"ROOT"点可以忽略)

也是像树状数组一样的,将大区间拆分为小的,查询时选取相应区间做指定运算就是了

关于操作和维护的信息

最垃圾的线段树支持的操作有:

1. 区间修改,
   • 区间加减(本篇博客唯一介绍的,进阶知识以后整理)
   • 区间乘除
   • 区间开方,就是把元素一一开方
   • 其他
2. 区间查询
3. 好像没了

最垃圾的线段树可以维护的信息有:

1. 区间和
2. 区间最小值
3. 区间最大值
4. 区间异或值
5. (好像没有区间乘积这样一种毒瘤操作,有了也没啥意义)
6. 其他

总而言之,线段树就是一种用来对数列进行花式维护的数据结构

写在前面:本篇博客主要用线段树维护区间和

关于线段树大致的具体原理

具体的,其原理如下:

• 首先我们要清楚,线段树是一种支持很多区间修改的NB结构

  作为树,它是一个二叉树(这点我们稍后谈到),常数大一点

• 既然是"线段"树,我们用每个节点对应一个区间,就像是上面图中的线段

  当然,根节点对应的区间就是整个区间,也就是整个数列

  在上面的图中,我们可以看到,每个节点在树上的形态实质就是线段,就是区间

  所以本文中"区间"和"节点"基本上是一个东西...

• 为了保证每个操作快捷的完成,我们将区间拆成子区间来递归操作,

  我们规定将一个区间二分,拆为两段,分别代替左右区间,

  拆分规则在这里给出:

  (mid=leftlfloor (l+r)/2 ight floor,[l,r] o[l,mid] | [mid+1,r])

  特殊的,当一个区间无法再进行拆分,就是说它的长度为1时,它就对应了一个叶节点,让其对应数列的一个元素

  易证得,将一个区间二分下去,其长度为1的区间个数一定等于区间长度,(看上面的两张图感性理解下啊...)

• 总结一下,每个节点对应一个区间,而其左右儿子分别对应该节点左半个区间和右半个区间

• 在维护简单信息(区间和,最大值,最小值等)时,我们发现这些值可以由子区间非常简单的合并得到

  比如sum(区间和),我们有(sum_{l,r}=sum_{l,mid}+sum_{mid+1,r}),

  其他信息不妨自己推

  这样,我们就可以用小区间维护大区间,每个节点就保存了对应当前区间的区间信息

  对于多种信息,可以多开数组或者直接开个结构体储存

  记住这个"小区间维护大区间",后面有用...

• 但是数据肯定不会只对区间([1,8])中([1,4],[7,8])这样的特殊的区间进行操作,

  这里他们特殊表现在他们自己可以表示为一个节点对应的区间,

  翻译一下,存在唯一节点,其对应区间恰是这些"特殊区间"

  就是说,操作的区间可能会涉及到多个节点,

  倘若递归到每一个叶节点进行操作...这样还不如朴素算法吧...

• 那么我们考虑用尽可能少的特殊区间表示操作区间,然后再将这些特殊区间合并为要操作的目标区间的值,合并细则参考小区间维护大区间时的细则

• 拆分与合并原理如下:

  我们在操作目标区间的时候,从根节点出发,就是从整个区间开始往下找目标区间

  当然,最方便的查找方式还是将区间二分,只要当前区间与目标区间有交集,就说明有继续分的价值,否则舍弃,

  这样一来,层层递归可以精确找到目标区间,再进行合并

  具体细则在这里给出:

  1. 判断当前区间是否包含在目标区间,如果是,则直接对区间进行操作,如果节点该区间长度为1,则(return)

     这样一来,我们可以精确操作所有区间,并一路把所有值更新

  2. 否则,二分出中间节点(mid=leftlfloor (l+r)/2 ight floor)

  3. 查看目标区间的左端点是否在(mid)左边(或是与(mid)重合),是的话表明在左子区间与目标区间有交集,那么我们可以递归左子区间进行操作,否则舍弃左边区间

     同理,判断(mid)是否在目标区间右端点左边,然后进行相应操作

     注意对于右端点的判断没有重合,否则会由于取整的神奇性质重复计算单点导致死循环,不妨自己证明

     落实到代码就是

     if(x<=mid) ...
     if(mid<y) ...
     

  4. 然后进行区间合并,如果是查询,那么就把递归上来的左右区间(如果目标区间同时与左右区间有交集的话)进行合并,递归并且(return)该值,如果是修改,就用小区间维护大区间,完成对大区间值的更新

  5. 完成操作

• 比如在区间([1,8])中操作([2,8]),

  我们分出的节点大概是:([1,8]),([1,4]),([5,8]),([1,2]),([3,4]),([5,6]),([7,8])以及剩下的叶节点

  来,跟着我...好好看,好好学,好好模拟成神仙...

  看图,这里线段代表元素,而不是点代表元素:

  

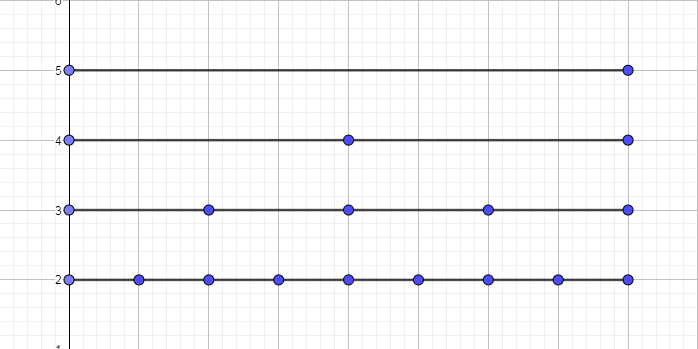
  首先,我们看到区间([1,8])

  发现并不是被目标区间包含,那么取(mid)

  发现它在左右子区间都有交集,递归,看到区间([1,4],[5,8])

  但是对于区间([1,4]),它仍然不是包含关系,且仍然左右都有交集,递归,([1,2],[3,4])

  对于区间([1,2]),继续递归,此时它的(mid)是(leftlfloordfrac{1+2}{2} ight floor=1)

  我们发现单点(1)并不包含在目标区间,舍弃不去递归,那么去递归有交集的单点(2),并直接操作

  同时发现有区间被包含,就是([3,4]),那么直接操作,并对它的整棵子树进行操作,一路维护到底,反正递归下去也全是包含关系

  递归回去发现([5,8])被包含,操作干就完了,

  这样一来,整个操作区间就被表示为单点(2),([3,4]),([5,8]),然后精确操作,并且暴力操作下去造福它们的子孙后代(滑稽)

  进行区间合并完成操作

• 至此,线段树的基本原理及实现思想结束

需要注意,在实现算法的途中,即建树过程中,假定当前编号为(k),

我们规定一个非叶节点的左儿子编号为(k*2),右儿子编号为(k*2+1),

这样十分方便建树

现在来看线段树空间复杂度

4倍,没别的

p.s.本来想写关于线段树3倍空间复杂度证明,但是其中感性理解太多

其实好像线段树是可以3倍空间的,但是听说某道题会RE所以保险起见开4倍吧...

看完最后一部分再回来想一想吧(downarrow downarrow downarrow)

朴素线段树函数代码

来看下每个部分的代码:

本代码维护区间和,有兴趣自己练最大值最小值,

(build)建造函数

用于建树,每次传参传的是节点编号(k),区间左端点(l),右端点(r)

思路:

• 递归操作,拆分区间,

• 如果区间长度为1说明对应到叶节点单一元素,直接赋值,

  注意这里线段树节点下标为(k)而单一元素则是(l),意为(k)号节点对应的是区间第(l)号元素,因为(l=r)所以可以对应到唯一元素

  赋值完成直接返回,不然会导致死循环,无限递而不归

• 如果长度不是1,继续按照二分法则拆分区间,递归回来以后用两个子区间的信息维护自己的信息

void build(int k,int l,int r){
	if(l==r){
		sum[k]=a[l];
		return ;
	}int mid=l+r>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
	sum[k]=sum[k<<1]+sum[k<<1|1];
}

insert修改函数,区间加

区间加上某个值

思路:

• 如果当前区间被包含,直接加,为什么这样加不妨自己证明,

  区间长度为1则(return)防止死循环

• 如果不被包含,拆分判断并在对应区间修改,修改递归完了就合并

void insert(int k,int l,int r,int x,int y,int v){
	if(x<=l&&r<=y)
		sum[k]+=(r-l+1)*v;
	if(l==r) return ;
	int mid=l+r>>1;
	if(x<=mid) insert(k<<1,l,mid,x,y,v);
	if(mid<y) insert(k<<1|1,mid+1,r,x,y,v);
	sum[k]=sum[k<<1]+sum[k<<1|1];
}

query查询函数

思路同(insert),只是需注意细节

比如(ret)一开始要初始化为0

int query(int k,int l,int r,int x,int y){
	if(x<=l&&r<=y)
		return sum[k];
	int mid=l+r>>1;
	int ret=0;
	if(x<=mid)
		ret+=query(k<<1,l,mid,x,y);
	if(mid<y)
		ret+=query(k<<1|1,mid+1,r,x,y);
	return ret;
}

ok,非常漂亮

来看时间复杂度

显而易见,线段树本身于"二分"这个东西有着不小的联系

所以一般来说,其操作是(O(mlog_2n))的,m是操作个数,n是区间长度

简单来说就是因为每次递归操作时只用归(log_2n)次,操作数又是m,那么得证

一切看上去美好而又理所当然

但是,我们考虑以下情况:

我们费了(log_2n)的时间去维护一个值,但是在查询的时候,一连几个区间用不到这个元素,这无疑造成了时间的浪费,

别小看这多出来的(log_2n),它可能要了你的小命,不仅仅是luogu上的30'

这在以线段树为工具的其他题目是十分要命的,

那么能不能在保存值的基础上,尽量的不用那些被更新但是不访问的变量呢?

考虑以下优化:

• 我们对于适当的区间,放上一种标记,使得未访问(这里的访问同时指插入和询问等多种区间操作)的节点不更新值,
• 就是假如区间([1,4])有一个新加的值,但我们并不访问,那就在这个节点上面记录一个值存多加了多少,对于其任何子区间,如([1,2],[3,4])等,不进行值的更新,

这样一来,就大大的加快了程序的运行,

运用了人不犯我我不犯人的重要思想

那么我们称这个东西为懒标记((Lazy-Tag)),
对于每个节点,可以有这样一个懒标记,储存当前这个(k)节点的每个元素加了(laz[k])的值,在访问时,给当前节点的(sum)加上(laz[k]*(r-l+1)),这样就是这个区间总的变化量,

注意,这个懒标记表示的是当前节点的儿子们需要加上的值,

也就是说,懒标记只对子区间进行修改,区间在被修改的同时,其对应区间懒标记也会被修改,表示当前节点修改过了,但是他的儿子们还没有修改,那么我们将这个值在(laz)数组中存着,以后再用,

但是用完以后一定要清零,表示我的儿子们已经加过了,不用再加一次了

比如对区间([3,4])加上4,那么就对于其(sum)加上4,对其懒标记加4,表示儿子们需要加的值多了4(因为毕竟可能之前有过标记),

那么在进一步操作时,将标记下传,将其所有子区间(sum)加上(len()就是(r-l+1)*laz),即为区间每个元素加完之后总的和,然后再将子区间(laz)也修改,这个操作就是说"当前节点儿子修改过了,当前节点的儿子的儿子需要修改了"

那么我们需要一个新的函数,即为标记下传函数(pushdown),后面讲,不要急,先看看在哪里用,再看怎么用,

那么有人要问,如果在多次操作中同一个节点区间的元素加了不同的值,如何处理?

就是说,如果在区间([1,3]),([2,4])中加了值,那么其中公共部分的标记如何处理呢?

其实不用担心,

• 每次在值的更新时,要先进行一步判断,判断当前区间是否被要修改的区间包含

• • 如果是,则直接进行加操作,并把相应标记加上对应值,直接(return),不对子区间进行操作,否则浪费时间还有可能死循环

  • 如果否,则说明现在处理的区间只是于目标区间存在交集,并不是所有位置都需要加,

    所以当前一层的懒标记并不能直接莽加,

• 考虑如果之前有标记的话,那么反正本次操作要用到子区间,那么不妨将之前存的标记进行下传,

  然后对子区间进行更新,

  然后再按照修改函数(insert)的区间拆分思想进行对于子区间的处理

  最后递归回来之后,对当前区间的(sum)用被更新过的子区间的(sum)进行更新,完成操作

来,如图模拟一下([1,3]),([2,4])的区间加,假设原来一点标记都没有,

首先,直接对区间([1,3])进行加操作,同时更新标记,如下图:

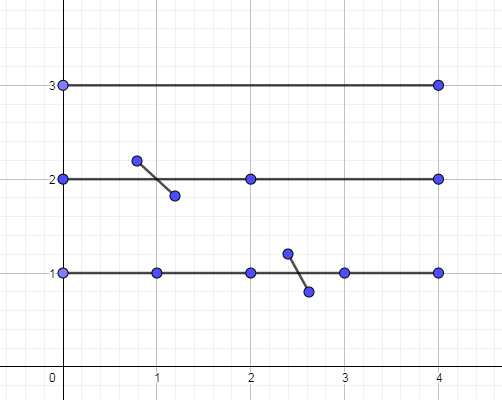
那么在第二次操作中,在递归区间([1,2])时,我们发现只需要更新叶节点2而并不是整个区间([1,2])

所以我们把其标记下传,传到两个子节点(在这个图中是叶子结点)上去:

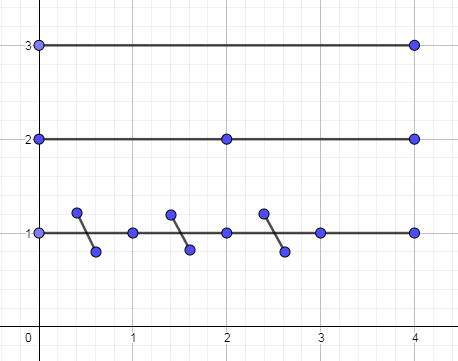
然后我们直接去找叶节点2,进行直接修改,

最后看右边的区间,发现([2,4])包含([3,4]),所以直接一波加操作猛如虎

最终结果如图:

当然,划线表示第一次的标记,/表示第二次的

如此一来,我们完成了区间加操作,

只得一提的是,叶子结点因为没有儿子,所以其懒标记没有实际意义,即使溢出也没关系,

以上是(pushdown)函数在区间修改中的应用,那么这个(pushdown)怎么实现呢?

• 先进行判断,如果标记为0就根本没有下传的必要,

• 如果不为0,则将其两个子节点的(sum)值加上(len(mid-l+1)或者(r-mid)*laz)

  至于这里为什么是(r-mid)不是(r-mid+1),因为右节点左端点是(mid+1),那么(r-(mid+1)+1)显然就是(r-mid)

• 再将子节点的(laz)加上当前节点的(laz)值,表示孩子,食大便了时代变了

• 最后将自己的(laz)清零

完成(pushdown)操作

代码如下:

void pushdown(int k,int l,int r){
	if(!laz[k]) return ;
	int mid=l+r>>1;
	sum[k<<1]+=(mid-l+1)*laz[k];
	sum[k<<1|1]+=(r-mid)*laz[k];
	laz[k<<1]+=laz[k];
	laz[k<<1|1]+=laz[k];
	laz[k]=0;
	return ;
}

当然还有算法是将标记永久化,

个人不喜欢,所以不用,毕竟消除标记方便多种运算的使用,就是同时支持区间加,乘,开方啥的,

于是我们将(O(nlog_2n))的复杂度优化成了...如果不是全都是单点修改的话...严格小于(O(nlog_2n))的复杂度

但是这可优化可是很大的(噘嘴)!

这就将最垃圾的线段树优化成了...

不是特别垃圾的基本线段树

所以说要在线段树的路上学习,要走的路还长得很

代码

结构体维护版本:

#include<iostream>
#include<cstdio>
using namespace std;
#define ci const int &
#define ll long long
const int N=100005;
int n,m;
struct node{
	ll sum,laz;
}nd[N<<2];
ll a[N];
inline void build(ci k,ci l,ci r){
	if(l==r){
		nd[k].sum=a[l];
		return ;
	}
	int mid=l+r>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
	nd[k].sum=nd[k<<1].sum+nd[k<<1|1].sum;
}
inline void pushdown(ci k,ci l,ci r){
	if(!nd[k].laz) return ;
	int mid=l+r>>1;
	nd[k<<1].sum+=(mid-l+1)*nd[k].laz;
	nd[k<<1|1].sum+=(r-mid)*nd[k].laz;
	nd[k<<1].laz+=nd[k].laz;
	nd[k<<1|1].laz+=nd[k].laz;
	nd[k].laz=0;
}
inline void insert(ci k,ci l,ci r,ci x,ci y,const ll &v){
	if(x<=l&&r<=y){
		nd[k].sum+=(r-l+1)*v;
		nd[k].laz+=v;
		return ;
	}
	pushdown(k,l,r);
	int mid=l+r>>1;
	if(x<=mid) insert(k<<1,l,mid,x,y,v);
	if(mid<y) insert(k<<1|1,mid+1,r,x,y,v);
	nd[k].sum=nd[k<<1].sum+nd[k<<1|1].sum;
}
inline ll find(ci k,ci l,ci r,ci x,ci y){
	if(x<=l&&r<=y) return nd[k].sum;
	pushdown(k,l,r);
	int mid=l+r>>1;
	ll ret=0;
	if(x<=mid) ret+=find(k<<1,l,mid,x,y);
	if(mid<y) ret+=find(k<<1|1,mid+1,r,x,y);
	return ret;
}
int main(){
	//...
	return 0;
}

数组维护版本:

#include<iostream>
#include<cstdio>
using namespace std;
#define ci const int &
#define ll long long
const int N=100005;
int n,m;
ll sum[N<<2];
ll laz[N<<2];
ll a[N];
inline void build(ci k,ci l,ci r){
	if(l==r){
		sum[k]=a[l];
		return ;
	}
	int mid=l+r>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
	sum[k]=sum[k<<1]+sum[k<<1|1];
}
inline void pushdown(ci k,ci l,ci r){
	if(!laz[k]) return ;
	int mid=l+r>>1;
	sum[k<<1]+=(mid-l+1)*laz[k];
	sum[k<<1|1]+=(r-mid)*laz[k];
	laz[k<<1]+=laz[k];
	laz[k<<1|1]+=laz[k];
	laz[k]=0;
}
inline void insert(ci k,ci l,ci r,ci x,ci y,const ll &v){
	if(x<=l&&r<=y){
		sum[k]+=(r-l+1)*v;
		laz[k]+=v;
		return ;
	}
	pushdown(k,l,r);
	int mid=l+r>>1;
	if(x<=mid) insert(k<<1,l,mid,x,y,v);
	if(mid<y) insert(k<<1|1,mid+1,r,x,y,v);
	sum[k]=sum[k<<1]+sum[k<<1|1];
}
inline ll find(ci k,ci l,ci r,ci x,ci y){
	if(x<=l&&r<=y) return sum[k];
	pushdown(k,l,r);
	int mid=l+r>>1;
	ll ret=0;
	if(x<=mid) ret+=find(k<<1,l,mid,x,y);
	if(mid<y) ret+=find(k<<1|1,mid+1,r,x,y);
	return ret;
}
int main(){
	//...
	return 0;
}

感受:

1. 对于部分人来说...好长的模板题呀!!!

   显然你没敲过树链剖分什么的...

2. 函数加上(inline),(const)和&可以更快,但(const)仅用于不修改其值的情况,是个常用的卡常技巧,这里我骚气地定义成了(ci)

   同样,因为计算机喜欢用二进制,所以位运算显然要快一些

那么前面整理的(ST)表,树状数组,线段树到底联系在哪,区别在哪?

先说(ST),其由于结构较简单,只能维护较简单的信息,也就求求最大值最小值

那么树状数组就要稍微好些,可以维护前缀和,前缀最大最小值,前缀积,

但是其缺陷就是在于只能维护"前缀",求和海星,然而求积的话,如果乘积较大需要取模,那么可能会出现这样一种东西（设查询区间(1sim x)前缀乘积函数值为(f(x)),模数为_rqy）:
(cfrac{f(r)\%\_rqy}{f(l-1)\%\_rqy})
然而众所周知,取模是不能除的,除非...你会一种叫逆元的东西...

还有区间最大最小值的问题,这根本没法求...

使用ta的唯一理由怕就是好写,代码短...
那么对于线段树...(坏笑)
几乎上面有限制的ta都能做
另外还可以求区间异或和,区间这那,超级方便,
对于区间(k)小值...想听听主席树吗...

线段树的一些有趣的性质(选学,其实完全可以不学...)

本部分内容仅对于二分法则为(mid=leftlfloordfrac{l+r}{2} ight floor)的线段树,实际上不这么分的也没几个...

p.s.这些东西本来都是空间复杂度证明中的内容,懒得证了

易得:对于区间长度为(2^n,nin Z),其节点个数是(2*n-1),不再议论,

那么如果区间长度不是(2)的整次幂...

对于任意的奇数长度区间,其左子区间一定比右子区间长

原因如下:
对于奇数区间,其右端点可以表示成如下状态:(l)(左端点)(+len)(奇数区间长度)(-1),

那么,其划分的区间就是([l,dfrac{2*l+len-1}{2}])

以及([dfrac{2*l+len-1}{2} +1,l+len-1])

化简:

([l,l+dfrac{len-1}{2}])

与([l+dfrac{len-1}{2}+1,l+len-1]),也就是([l+dfrac{len+1}{2},l+len-1])

整理一下两边的区间长度可得:

左:(dfrac{len-1}{2}+1),即为(dfrac{len+1}{2})

右:(len-1-dfrac{len+1}{2}),即为(dfrac{len-1}{2})

所以左边的区间长度实际上要大1,

从而顺便我们得出另一个结论,对于任意一个区间,其左子区间长度减右子区间长度不超过1.

顺便说一句,线段树也可以动态开点,这样的话每个节点还需要存左右儿子编号

结尾

整这篇博客时间较久,不如...

点个关注或者硬币都是可以的

点个赞?