一 线性回归理论概述
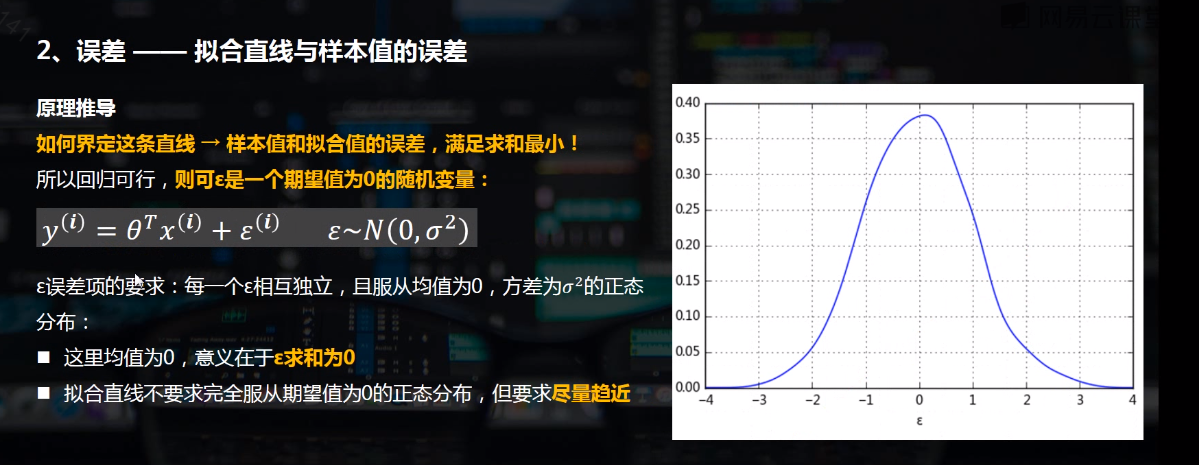
回归,指研究一组随机变量(Y1 ,Y2 ,…,Yi)和另一组(X1,X2,…,Xk)变量之间关系的统计分析方法。



from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit( x[ : ,np.newaxis] )
model.coef_
model.intercept_
model.predict( x[ : , np.newaxis ] )
二 线性回归模型评估
判断回归模型好坏
from sklearn import metrics
metrics下有很多方法,SSE,SSR,SST等等,用到的时候再说吧
model.score() --> R-square(确定系数) 越接近于1,拟合效果越好。 R-square = SSR/SST
SSE(和方差、误差平方和):The sum of squares due to error
MSE(均方差、方差):Mean squared error
RMSE(均方根、标准差):Root mean squared error
R-square(确定系数) Coefficient of determination
三 KNN邻近算法
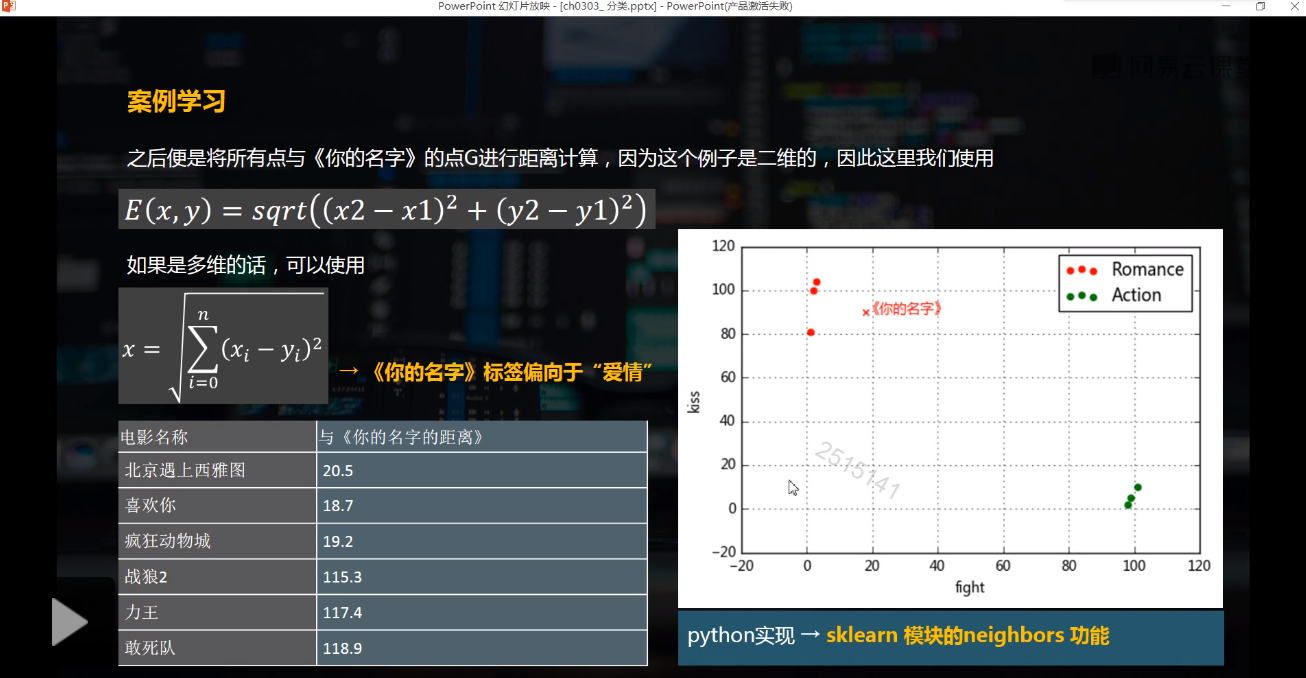
邻近算法,或者说K最近邻(kNN,k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。
kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 kNN方法在类别决策时,只与极少量的相邻样本有关。由于kNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,kNN方法较其他方法更为适合。
from sklearn import neighbors
knn = neighbors.KNeighborsClassifier()
knn.fit()
knn.predict()
from sklearn import datasets
iris = datasets.load_iris()
iris.feature_names
iris.target_names
四 聚类
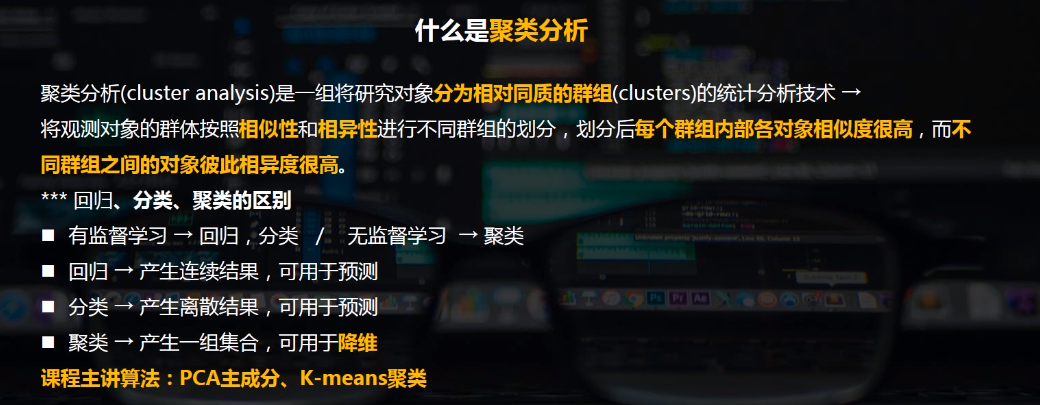
聚类分析指将物理或抽象对象的集合 分组为由类似的对象组成的多个类的分析过程
聚类与分类的不同在于,聚类所要求划分的类是未知的。
聚类是将 数据分类到不同的类或者簇这样的一个过程,所以同一个簇中的对象有很大的相似性,而不同簇间的对象有很大的相异性。
从机器学习的角度讲,簇相当于隐藏模式。聚类是搜索簇的 无监督学习过程。与分类不同, 无监督学习不依赖预先定义的类或带类标记的训练实例,需要由聚类学习算法自动确定标记,而分类学习的实例或 数据对象有类别标记。聚类是观察式学习,而不是示例式的学习。
聚类分析是一种探索性的分析,在分类的过程中,人们不必事先给出一个分类的标准,聚类分析能够从样本数据出发,自动进行分类。聚类分析所使用方法的不同,常常会得到不同的结论。不同研究者对于同一组数据进行聚类分析,所得到的聚类数未必一致。
1 PCA主成分分析
无监督学习
原理挺复杂,用到了矩阵相关的数学知识,,有机会在细看吧




from sklearn.decomposition import PCA
pca = PCA(n_components=5)
new_data = pca.fit_transform(data)
pct.components_ 特征向量 (5,x)
pca.explained_variance_ 特征值?/ pca的方法explained_variance_ratio_计算了每个特征方差贡献率,所有总和为1,explained_variance_ 为方差值。 这里不太明白
2 K-means 聚类
无监督学习
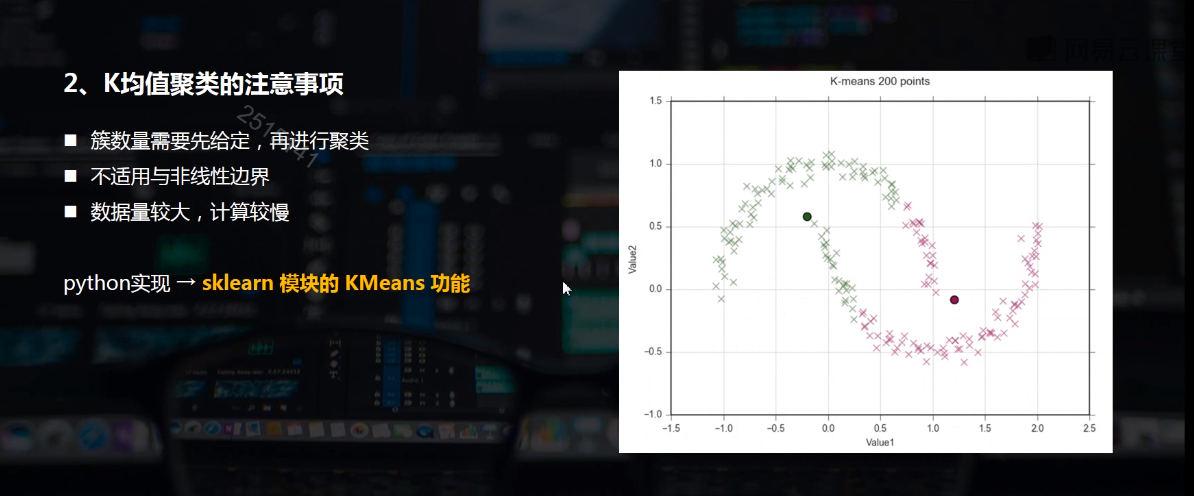
K-MEANS算法是输入聚类个数k,以及包含 n个数据对象的数据库,输出满足方差最小标准k个聚类的一种算法。k-means 算法接受输入量 k ;然后 将n个数据对象划分为 k个聚类以便使得所获得的聚类满足:同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。
聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”(引力中心)来进行计算的。

from sklearn.datasets.samples_generator import make_blobs
x,y = make_blobs(n_samples=200,n_features=2,centers=5,cluster_std=1) # x → 生成数据值, y → 生成数据对应的类别标签
from sklearn.cluster import KMeans
kmean = KMeans(n_clusters=5
kmeans.fit(x)
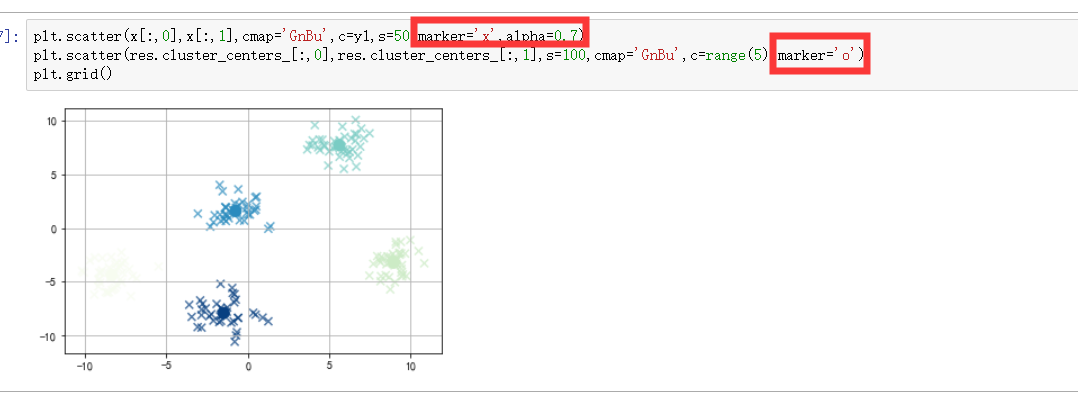
y1 = kmean.predict(x)
kmeans.cluster_centers_
五 蒙特卡罗模拟理论
是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。
from matplotlib.patches import Circle
circle = Circle(xy = (a,b),radius = r, alpha = 0.5 ,color = 'gray')
axes.add_patch(circle)
plt.fill_between() -->用linspace