Write a program to find the strongly connected components in a digraph.
Format of functions:
void StronglyConnectedComponents( Graph G, void (*visit)(Vertex V) );
where Graph is defined as the following:
typedef struct VNode *PtrToVNode;
struct VNode {
Vertex Vert;
PtrToVNode Next;
};
typedef struct GNode *Graph;
struct GNode {
int NumOfVertices;
int NumOfEdges;
PtrToVNode *Array;
};
Here void (*visit)(Vertex V) is a function parameter that is passed into StronglyConnectedComponents to handle (print with a certain format) each vertex that is visited. The function StronglyConnectedComponents is supposed to print a return after each component is found.
Sample program of judge:
#include <stdio.h>
#include <stdlib.h>
#define MaxVertices 10 /* maximum number of vertices */
typedef int Vertex; /* vertices are numbered from 0 to MaxVertices-1 */
typedef struct VNode *PtrToVNode;
struct VNode {
Vertex Vert;
PtrToVNode Next;
};
typedef struct GNode *Graph;
struct GNode {
int NumOfVertices;
int NumOfEdges;
PtrToVNode *Array;
};
Graph ReadG(); /* details omitted */
void PrintV( Vertex V )
{
printf("%d ", V);
}
void StronglyConnectedComponents( Graph G, void (*visit)(Vertex V) );
int main()
{
Graph G = ReadG();
StronglyConnectedComponents( G, PrintV );
return 0;
}
/* Your function will be put here */
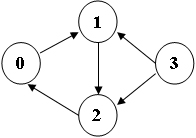
Sample Input (for the graph shown in the figure):
4 5
0 1
1 2
2 0
3 1
3 2
Sample Output:
3
1 2 0
Note: The output order does not matter. That is, a solution like
0 1 2
3
is also considered correct.
找图的强连通分量,题目中的建图的函数没给出定义,实际使用邻接表。
由于边数很少可以考虑先求所有边可达矩阵,mp[i][j]为1,表示存在i到j的路径,可以用邻接矩阵的n次方求得。然后排着判断即可,一个强连通分量里的点必定都是相互可达的。
代码:
#include <stdio.h> #include <stdlib.h> #define MaxVertices 10 /* maximum number of vertices */ typedef int Vertex; /* vertices are numbered from 0 to MaxVertices-1 */ typedef struct VNode *PtrToVNode; struct VNode { Vertex Vert; PtrToVNode Next; }; typedef struct GNode *Graph; struct GNode { int NumOfVertices; int NumOfEdges; PtrToVNode *Array; }; Graph ReadG() { /* details omitted */ int a,b; Graph G = (Graph)malloc(sizeof(GNode)); scanf("%d%d",&G -> NumOfVertices,&G -> NumOfEdges); G -> Array = (PtrToVNode *)malloc(sizeof(PtrToVNode) * G -> NumOfVertices); for(int i = 0;i < G -> NumOfVertices;i ++) { G -> Array[i] = NULL; } for(int i = 0;i < G -> NumOfEdges;i ++) { scanf("%d%d",&a,&b); PtrToVNode p = (PtrToVNode)malloc(sizeof(VNode)); p -> Vert = b; p -> Next = G -> Array[a]; G -> Array[a] = p; } return G; } void PrintV( Vertex V ) { printf("%d ", V); } void StronglyConnectedComponents( Graph G, void (*visit)(Vertex V) ); int main() { Graph G = ReadG(); StronglyConnectedComponents( G, PrintV ); return 0; } /* Your function will be put here */ void StronglyConnectedComponents( Graph G, void (*visit)(Vertex V) ) { int mp[MaxVertices][MaxVertices] = {0},num = G -> NumOfVertices; int vis[MaxVertices] = {0}; for(int i = 0;i < num;i ++) { PtrToVNode p = G -> Array[i]; while(p) { mp[i][p -> Vert] = 1; p = p -> Next; } } for(int k = 0;k < num;k ++) { for(int i = 0;i < num;i ++) { for(int j = 0;j < num;j ++) { if(mp[i][k] && mp[k][j]) mp[i][j] = 1; //for(int l = 0;l < num;l ++) mp[i][j] |= mp[i][l] * mp[l][j]; //上一句可替换为这一句 可达矩阵的n - 1次方可以求出任意一点到另一点是否可达 } } } for(int i = 0;i < num;i ++) { if(vis[i]) continue; visit(i); vis[i] = 1; for(int j = 0;j < num;j ++) { if(!vis[j] && mp[i][j] && mp[j][i]) { vis[j] = 1; visit(j); } } putchar(' '); } }