k近邻法的C++实现：kd树

1.k近邻算法的思想

给定一个训练集，对于新的输入实例，在训练集中找到与该实例最近的k个实例，这k个实例中的多数属于某个类，就把该输入实例分为这个类。

因为要找到最近的k个实例，所以计算输入实例与训练集中实例之间的距离是关键！

k近邻算法最简单的方法是线性扫描，这时要计算输入实例与每一个训练实例的距离，当训练集很大时，非常耗时，这种方法不可行，为了提高k近邻的搜索效率，常常考虑使用特殊的存储结构存储训练数据，以减少计算距离的次数，具体方法很多，这里介绍实现经典的kd树方法。

2.构造kd树

kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构，kd树是二叉树。

下面举例说明：

给定一个二维空间的数据集: T = {(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)},构造一个平衡kd树。

• 根结点对应包含数据集T的矩形选择x⁽¹⁾ 轴，6个数据点的x⁽¹⁾ 坐标的中位数是7，以超平面x⁽¹⁾ = 7将空间分为左右两个子矩形（子结点）
• 左矩形以x⁽²⁾ = 4为中位数分为两个子矩形
• 右矩形以x⁽²⁾ = 6 分为两个子矩形
• 如此递归，直到两个子区域没有实例存在时停止

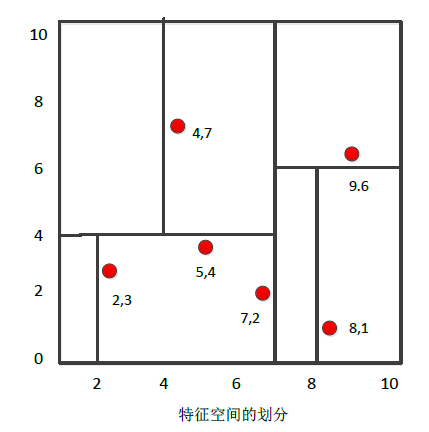
构造的kd树如下：

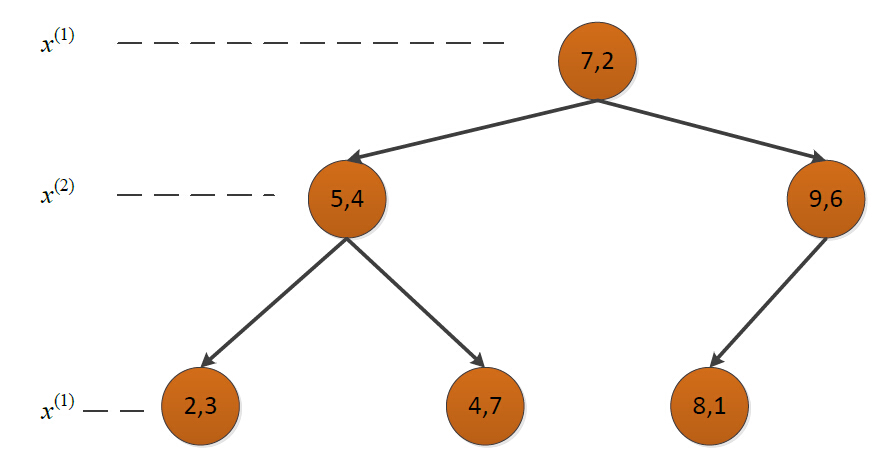
3.利用kd树搜索最近邻

输入：已构造的kd树；目标点x;

输出：x的最近邻

• 在kd树中找出包含目标点x的叶结点：从根结点出发，递归的向下访问kd树，若目标点x的当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点，直到子结点为叶结点为止。
• 以此叶结点为“当前最近点”
• 递归地向上回退，在每个结点进行以下操作：（a）如果该结点保存的实例点比当前最近点距离目标点更近，则以该实例点为“当前最近点”;

  (b)当前最近点一定存在于某结点一个子结点对应的区域，检查该子结点的父结点的另
  一子结点对应区域是否有更近的点（即检查另一子结点对应的区域是否与以目标点为球
  心、以目标点与“当前最近点”间的距离为半径的球体相交）；如果相交，可能在另一
  个子结点对应的区域内存在距目标点更近的点，移动到另一个子结点，接着递归进行最
  近邻搜索；如果不相交，向上回退

• 当回退到根结点时，搜索结束，最后的“当前最近点”即为x的最近邻点。

4.C++实现

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <cmath>
using namespace std;




struct KdTree{
    vector<double> root;
    KdTree* parent;
    KdTree* leftChild;
    KdTree* rightChild;
    //默认构造函数
    KdTree(){parent = leftChild = rightChild = NULL;}
    //判断kd树是否为空
    bool isEmpty()
    {
        return root.empty();
    }
    //判断kd树是否只是一个叶子结点
    bool isLeaf()
    {
        return (!root.empty()) && 
            rightChild == NULL && leftChild == NULL;
    }
    //判断是否是树的根结点
    bool isRoot()
    {
        return (!isEmpty()) && parent == NULL;
    }
    //判断该子kd树的根结点是否是其父kd树的左结点
    bool isLeft()
    {
        return parent->leftChild->root == root;
    }
    //判断该子kd树的根结点是否是其父kd树的右结点
    bool isRight()
    {
        return parent->rightChild->root == root;
    }
};

int data[6][2] = {{2,3},{5,4},{9,6},{4,7},{8,1},{7,2}};

template<typename T>
vector<vector<T> > Transpose(vector<vector<T> > Matrix)
{
    unsigned row = Matrix.size();
    unsigned col = Matrix[0].size();
    vector<vector<T> > Trans(col,vector<T>(row,0));
    for (unsigned i = 0; i < col; ++i)
    {
        for (unsigned j = 0; j < row; ++j)
        {
            Trans[i][j] = Matrix[j][i];
        }
    }
    return Trans;
}

template <typename T>
T findMiddleValue(vector<T> vec)
{
    sort(vec.begin(),vec.end());
    auto pos = vec.size() / 2;
    return vec[pos];
}


//构建kd树
void buildKdTree(KdTree* tree, vector<vector<double> > data, unsigned depth)
{

    //样本的数量
    unsigned samplesNum = data.size();
    //终止条件
    if (samplesNum == 0)
    {
        return;
    }
    if (samplesNum == 1)
    {
        tree->root = data[0];
        return;
    }
    //样本的维度
    unsigned k = data[0].size();
    vector<vector<double> > transData = Transpose(data);
    //选择切分属性
    unsigned splitAttribute = depth % k;
    vector<double> splitAttributeValues = transData[splitAttribute];
    //选择切分值
    double splitValue = findMiddleValue(splitAttributeValues);
    //cout << "splitValue" << splitValue  << endl;

    // 根据选定的切分属性和切分值，将数据集分为两个子集
    vector<vector<double> > subset1;
    vector<vector<double> > subset2;
    for (unsigned i = 0; i < samplesNum; ++i)
    {
        if (splitAttributeValues[i] == splitValue && tree->root.empty())
            tree->root = data[i];
        else
        {
            if (splitAttributeValues[i] < splitValue)
                subset1.push_back(data[i]);
            else
                subset2.push_back(data[i]);
        }
    }

    //子集递归调用buildKdTree函数

    tree->leftChild = new KdTree;
    tree->leftChild->parent = tree;
    tree->rightChild = new KdTree;
    tree->rightChild->parent = tree;
    buildKdTree(tree->leftChild, subset1, depth + 1);
    buildKdTree(tree->rightChild, subset2, depth + 1);
}

//逐层打印kd树
void printKdTree(KdTree *tree, unsigned depth)
{
    for (unsigned i = 0; i < depth; ++i)
        cout << "	";
            
    for (vector<double>::size_type j = 0; j < tree->root.size(); ++j)
        cout << tree->root[j] << ",";
    cout << endl;
    if (tree->leftChild == NULL && tree->rightChild == NULL )//叶子节点
        return;
    else //非叶子节点
    {
        if (tree->leftChild != NULL)
        {
            for (unsigned i = 0; i < depth + 1; ++i)
                cout << "	";
            cout << " left:";
            printKdTree(tree->leftChild, depth + 1);
        }
            
        cout << endl;
        if (tree->rightChild != NULL)
        {
            for (unsigned i = 0; i < depth + 1; ++i)
                cout << "	";
            cout << "right:";
            printKdTree(tree->rightChild, depth + 1);
        }
        cout << endl;
    }
}


//计算空间中两个点的距离
double measureDistance(vector<double> point1, vector<double> point2, unsigned method)
{
    if (point1.size() != point2.size())
    {
        cerr << "Dimensions don't match！！" ;
        exit(1);
    }
    switch (method)
    {
        case 0://欧氏距离
            {
                double res = 0;
                for (vector<double>::size_type i = 0; i < point1.size(); ++i)
                {
                    res += pow((point1[i] - point2[i]), 2);
                }
                return sqrt(res);
            }
        case 1://曼哈顿距离
            {
                double res = 0;
                for (vector<double>::size_type i = 0; i < point1.size(); ++i)
                {
                    res += abs(point1[i] - point2[i]);
                }
                return res;
            }
        default:
            {
                cerr << "Invalid method!!" << endl;
                return -1;
            }
    }
}
//在kd树tree中搜索目标点goal的最近邻
//输入：目标点；已构造的kd树
//输出：目标点的最近邻
vector<double> searchNearestNeighbor(vector<double> goal, KdTree *tree)
{
    /*第一步：在kd树中找出包含目标点的叶子结点：从根结点出发，
    递归的向下访问kd树，若目标点的当前维的坐标小于切分点的
    坐标，则移动到左子结点，否则移动到右子结点，直到子结点为
    叶结点为止,以此叶子结点为“当前最近点”
    */
    unsigned k = tree->root.size();//计算出数据的维数
    unsigned d = 0;//维度初始化为0，即从第1维开始
    KdTree* currentTree = tree;
    vector<double> currentNearest = currentTree->root;
    while(!currentTree->isLeaf())
    {
        unsigned index = d % k;//计算当前维
        if (currentTree->rightChild->isEmpty() || goal[index] < currentNearest[index])
        {
            currentTree = currentTree->leftChild;
        }
        else
        {
            currentTree = currentTree->rightChild;
        }
        ++d;
    }
    currentNearest = currentTree->root;

    /*第二步：递归地向上回退， 在每个结点进行如下操作：
    (a)如果该结点保存的实例比当前最近点距离目标点更近，则以该例点为“当前最近点”
    (b)当前最近点一定存在于某结点一个子结点对应的区域，检查该子结点的父结点的另
    一子结点对应区域是否有更近的点（即检查另一子结点对应的区域是否与以目标点为球
    心、以目标点与“当前最近点”间的距离为半径的球体相交）；如果相交，可能在另一
    个子结点对应的区域内存在距目标点更近的点，移动到另一个子结点，接着递归进行最
    近邻搜索；如果不相交，向上回退*/

    //当前最近邻与目标点的距离
    double currentDistance = measureDistance(goal, currentNearest, 0);

    //如果当前子kd树的根结点是其父结点的左孩子，则搜索其父结点的右孩子结点所代表
    //的区域，反之亦反
    KdTree* searchDistrict;
    if (currentTree->isLeft())
    {
        if (currentTree->parent->rightChild == NULL)
            searchDistrict = currentTree;
        else
            searchDistrict = currentTree->parent->rightChild;
    }
    else
    {
        searchDistrict = currentTree->parent->leftChild;
    }

    //如果搜索区域对应的子kd树的根结点不是整个kd树的根结点，继续回退搜索
    while (searchDistrict->parent != NULL)
    {
        //搜索区域与目标点的最近距离
        double districtDistance = abs(goal[(d+1)%k] - searchDistrict->parent->root[(d+1)%k]);

        //如果“搜索区域与目标点的最近距离”比“当前最近邻与目标点的距离”短，表明搜索
        //区域内可能存在距离目标点更近的点
        if (districtDistance < currentDistance )//&& !searchDistrict->isEmpty()
        {

            double parentDistance = measureDistance(goal, searchDistrict->parent->root, 0);

            if (parentDistance < currentDistance)
            {
                currentDistance = parentDistance;
                currentTree = searchDistrict->parent;
                currentNearest = currentTree->root;
            }
            if (!searchDistrict->isEmpty())
            {
                double rootDistance = measureDistance(goal, searchDistrict->root, 0);
                if (rootDistance < currentDistance)
                {
                    currentDistance = rootDistance;
                    currentTree = searchDistrict;
                    currentNearest = currentTree->root;
                }
            }
            if (searchDistrict->leftChild != NULL)
            {
                double leftDistance = measureDistance(goal, searchDistrict->leftChild->root, 0);
                if (leftDistance < currentDistance)
                {
                    currentDistance = leftDistance;
                    currentTree = searchDistrict;
                    currentNearest = currentTree->root;
                }
            }
            if (searchDistrict->rightChild != NULL)
            {
                double rightDistance = measureDistance(goal, searchDistrict->rightChild->root, 0);
                if (rightDistance < currentDistance)
                {
                    currentDistance = rightDistance;
                    currentTree = searchDistrict;
                    currentNearest = currentTree->root;
                }
            }
        }//end if

        if (searchDistrict->parent->parent != NULL)
        {
            searchDistrict = searchDistrict->parent->isLeft()? 
                            searchDistrict->parent->parent->rightChild:
                            searchDistrict->parent->parent->leftChild;
        }
        else
        {
            searchDistrict = searchDistrict->parent;
        }
        ++d;
    }//end while
    return currentNearest;
}

int main()
{
    vector<vector<double> > train(6, vector<double>(2, 0));
    for (unsigned i = 0; i < 6; ++i)
        for (unsigned j = 0; j < 2; ++j)
            train[i][j] = data[i][j];

    KdTree* kdTree = new KdTree;
    buildKdTree(kdTree, train, 0);

    printKdTree(kdTree, 0);

    vector<double> goal;
    goal.push_back(3);
    goal.push_back(4.5);
    vector<double> nearestNeighbor = searchNearestNeighbor(goal, kdTree);
    vector<double>::iterator beg = nearestNeighbor.begin();
    cout << "The nearest neighbor is: ";
    while(beg != nearestNeighbor.end()) cout << *beg++ << ",";
    cout << endl;
    return 0;
}

5. 运行

下面是用上面举例构造的kd树求点(3,4.5)的最近邻：

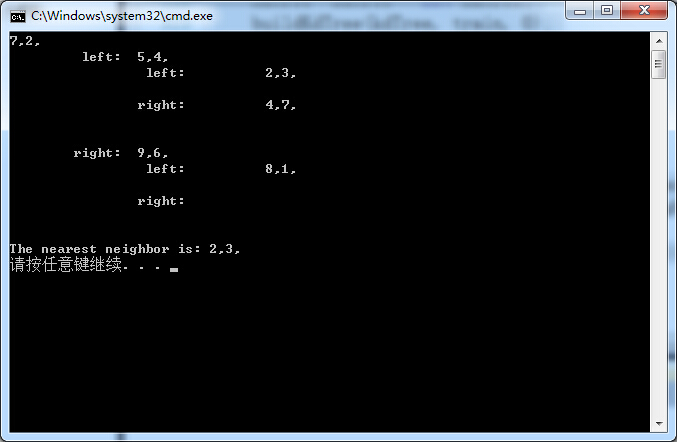
参考文献：李航《统计学习方法》，维基百科