背包九讲
1. 01背包
- 题目:

-
分析:
动态规划也就是一种用子问题去最优化原问题的策略。所以作为非常简单但重要的01背包问题,也是先考虑子问题。我们要求考虑 n 个物品装在容量为 V 的背包中的最大价值,
很容易想到其子问题就是
① n-1 个物品装在未装第n个物品容量为 V 的背包中的最大价值。
② **n-1 ** 个物品装在已经装了第n个物品容量为 V-w[i] 的背包中的最大价值。
我们可以细想一下,
-
考虑第1 个物品时,我们用算出来背包装它和背包不装它的最优解,
-
对于第2个物品我们在子问题最优解确定的基础上(即前1个物品时的最优解确定)比较背包装2的基础上装1和背包不装2时装1的最优解。
-
对于3物品,我们考虑背包装3的基础上考虑1和2和背包不装3时考虑1和2的最优解。
-
......
-
对于第n个物品,我们比较背包装n的基础上考虑前n-1个物品的价值和背包不装n时考虑前n-1个物品的价值,得到最优解。
-
-
代码:
#include<iostream> using namespace std; typedef long long ll; const int MA=1e3+5; int w[MA],v[MA],dp[MA][MA]; int main() { int n,V; cin>>n>>V; for(int i=0;i<=n;++i){ for(int j=0;j<=V;++j){ dp[i][j]=0; } } for(int i=1;i<=n;++i)cin>>w[i]>>v[i]; for(int i=1;i<=n;++i){ for(int j=0;j<=V;++j){ if(j>=w[i])dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]); else dp[i][j]=dp[i-1][j]; } } cout<<dp[n-1][V]<<endl; return 0; }2 空间复杂度优化
#include<iostream> using namespace std; const int MA=1e3+5; int w[MA],v[MA]; int dp[MA]; int main() { int n,V; cin>>n>>V; for(int i=1;i<=n;++i)cin>>w[i]>>v[i]; for(int i=1;i<=n;++i){ for(int j=V;j>=w[i];--j){ dp[j]=max(dp[j],dp[j-w[i]]+v[i]); } } cout<<dp[V]<<endl; return 0; }
完全背包问题
- 题目:

-
分析:
看玩题目我们其实已经想到将完全背包看作01背包问题,所以我们要想办法实现每个物品可以取多次。在这里我们要深入理解01背包的代码(建议回上面看看二维的01 背包核心代码)。
//初版 for(int i=1;i<=n;++i){ for(int j=0;j<=V;++j){ if(j>=w[i])dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]); else dp[i][j]=dp[i-1][j]; } } //空间复杂度优化 for(int i=1;i<=n;++i){ for(int j=V;j>=w[i];--j){ dp[j]=max(dp[j],dp[j-w[i]]+v[i]); } }理解01背包代码:对 i 的遍历,表面就是考虑每个物品。其实可以理解为第 i 轮更新各个容量时的最优解。这里第二层循环是对 j 的,注意方向是从 0 到 V。仔细看执行语句发现 j < w[i] (容量装不下第 i 个物品)dp[i ] [ j ]直接复制上一轮更新的结果 dp[ i-1 ] [ j ]。所以实际对 j 的遍历可以主要看作是 从 w[i] 到 V (当背包还剩余这些容量时),由上一轮的结果转移来。这样就保证在两轮更新里不会重复选择同一物品两次。而滚动数组写法时由 V 到 w[ i ] ,是因为这种写完无法直接找到对应的上一轮中的值,但因为未在新一轮更新的位置仍然然保存的是上一轮的结果,所以为了达到不会选择同一物品两次,我们就让容量从后往前处理,因为转移到该容量 j 的位置 j - w [ i ] 在 j 前面,还是本轮更新还未处理的位置,保存上一轮更新结果。
由上面的分析我们更了解01背包的思路。完全背包是可以重复取与01背包恰好要求相反,所以与01背包代码实现思路一样,只是有一点改动使其允许多次取同一物品。
完全背包的改动:
对于滚动数组写法,我们第二次循环将遍历方向改为从w[ i ] 到 V。为什么要这么改呢?因为每一轮结束后各位置保存该容量下的最优解,下一轮更新中因为转移到容量 j 的位置 j - w [ i ] 在 j 前面,也就是说在第 i 轮遍历 ( 处理第 i 个物品 ) 中, j 位置的值被j - w[ i ] 位置的值更新,j - w[ i ] 位置 也 被 其 前 面 的( j - w[ i ] ) - w[ i ] 位置更新,一直向前都是如此,所以第j位更新就是多次选取第 i 个物品的结果,也就实现了考虑对每个物品多次选取的情况。
for(int i=1;i<=n;++i){ for(int j=0;j<=V;++j){ if(j>=w[i])dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i]); else dp[i][j]=dp[i-1][j]; } }对于没有优化的写法,在第 i 轮,如果容量装不下第 i 个物品(j < w [ i ] )就直接让第 i 轮容量为 j 的最优解等于第 i - 1 轮更新时 j 的最优解。装得下就比较上一轮 j 位的最优解和本轮j - w[ i ] 位的最优解。
-
代码:
#include<iostream> using namespace std; typedef long long ll; const int MA=1e3+5; int w[MA],v[MA],dp[MA][MA]; int main() { int n,V; cin>>n>>V; for(int i=0;i<=n;++i){ for(int j=0;j<=V;++j)dp[i][j]=0; } for(int i=1;i<=n;++i){ cin>>w[i]>>v[i]; } for(int i=1;i<=n;++i){ for(int j=0;j<=V;++j){ if(j>=w[i])dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i]); else dp[i][j]=dp[i-1][j]; } } cout<<dp[n][V]<<endl; return 0; }#include<iostream> using namespace std; typedef long long ll; const int MA=1e3+5; int w[MA],v[MA]; int dp[MA]; int main() { int n,V; cin>>n>>V; for(int i=0;i<=V;++i){ dp[i]=0; } for(int i=1;i<=n;++i){ cin>>w[i]>>v[i]; } for(int i=1;i<=n;++i){ for(int j=w[i];j<=V;j++){ dp[j]=max(dp[j],dp[j-w[i]]+v[i]); } } cout<<dp[V]<<endl; return 0; } -
完全背包必须装满情况:
在上面完全背包上做以下改动就可以实现将这个问题转化为普通完全背包求解
①要求背包必须装满 求最大值
把f[0]初始化为0,其余初始化为(-∞)
②要求背包必须装满 求最小值
把f[0]初始化为0,其余初始化为(∞)
理解: 当要求最大值时,如上操作后,所有从非空推上来的值都是在(-∞)的基础上增加的,还是很小的值,在比较过程中都不会被取到,最后只有从dp[0]推上来的值都保留下来,比较其中的最值为答案。注意这里的从0推上来,是因为我们dp过程是在原容量上减的,所以背包容量可以到0即从0推上去的状态就都是将背包装满的。求最小值同理。
多重背包问题
- 题目:

-
分析:
对每个物品,如果 w*s >V (就是这个物品总体积大于背包容量,可以看作无限供应,用完全背包处理),而其他的物品可以用二进制优化,将w分为几个小部分,简化了处理量。
/*大雪菜代码(2进制优化)*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<string>
using namespace std;
typedef long long ll;
const int MA=2e3+5;
int dp[MA];
struct Good
{
int w,v;
};
vector<Good> goods;
int main()
{
int n,V;
cin>>n>>V;
for(int i = 1;i <= n; ++ i){
int w, v, s;
cin >> w >> v >> s;
for(int k = 1; k <= s; k *= 2){
s -= k;
goods.push_back({w * k, v * k});
}
if(s > 0)goods.push_back({w * s, v * s});
}
for(auto good : goods){
for(int j = V; j >= good.w; -- j){
dp[j] = max(dp[j], dp[j - good.w] + good.v);
}
}
cout<<dp[V]<<endl;
return 0;
}
#include<iostream>
using namespace std;
typedef long long ll;
const int MA=3e3+5;
int w[MA],v[MA],num[MA];
int dp[MA];
int n,V,ans;
void bag01(int tw,int tv)//01背包
{
for(int j=V ; j >= tw; --j){
dp[j]=max(dp[j],dp[j-tw]+tv);
}
}
void bagcom(int tw,int tv)//完全背包
{
for(int j=tw;j<=V;++j){
dp[j]=max(dp[j],dp[j-tw]+tv);
}
}
int main()
{
int k=1;
int nCount=0;
cin>>n>>V;
for(int i=1;i<=V;++i)dp[i]=0;
for(int i=1;i<=n;++i){
cin>>w[i]>>v[i]>>num[i];
}
for(int i=1;i<=n;++i){
if(w[i]*num[i] >= V){//原则上无限供应
bagcom(w[i],v[i]);//就看做完全背包题
}
else{
int k=1; //记录选择数量
int nCount = num[i];//这个物品最大数量
while(k <= nCount){//一直可以选
bag01(k*w[i],k*v[i]);
nCount -= k;
k*=2;
}
bag01(nCount * w[i] , nCount * v[i]);//最后再处理一下
}
}
cout<<dp[V]<<endl;
return 0;
}
单调队列优化
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N = 2e4+5;
int dp[N];
int n, m, v, w, c;
int q[N], h = 0, t = -1;
int val(int u, int k){
return dp[u + k * v] - k * w;
}
int main()
{
scanf("%d%d",&n ,&m);
memset(dp, 0xcf, sizeof(dp));
dp[0] = 0;
for(int i = 1; i <= n; ++ i){
scanf("%d%d%d",&v, &w, &c);
for(int u = 0; u < v; ++ u){ // u:余数分类
h = 0, t = -1;
int maxp = (m - u) / v;
//处理队列
for(int k = maxp - 1; k >= max(0, maxp - c); -- k){ //队列准备(i - 1维)
while(h <= t && val(u, k) >= val(u, q[t])) t --;
q[++ t] = k;
}
//更新+删
for(int p = maxp; p >= 0; -- p){
while(h <= t && p - q[h] < 1) h ++;
if(h <= t) dp[u + p * v] = max(dp[u + p * v], p * w + val(u, q[h]));
if(p - c - 1 >= 0){ //这是为p - 1的位置更新决策集合,所以(p - 1) - c >= 0
while(h <= t && val(u, p - c - 1) >= val(u, q[t])) t --;
q[++ t] = p - c - 1;
}
}
}
}
int res = 0;
for(int i = 1; i <= m; ++ i)
res = max(res, dp[i]);
printf("%d
", res);
return 0;
}
代码2:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<string>
using namespace std;
typedef long long ll;
const int MA=2e3+5;
int n,V;
int dp[MA],g[MA],q[MA];
int main()
{
cin>>n>>V;
for(int i=0;i<n;++i){ //( 0 ~ n )遍历每一个物品
//int c,w,s;
int w,v,s;
cin>>w>>v>>s;
memcpy(g,dp,sizeof(dp));//g[]中保存dp数组上一轮的情况
for(int j = 0; j < w; ++j){ //( 0 ~ w ) 按 % w 余数分组
int hh=0,tt=-1;
for(int k = j; k <= V; k += w){//从余数开始每次加 w,遍历这个余数组的每一个值(用k表示)。
dp[k] = g[k];
if(hh <= tt && k - s*w > q[hh]) hh++;
if(hh <= tt) dp[k]=max(dp[k], g[q[hh]] + (k - q[hh]) /w *v);
while(hh <= tt && g[q[tt]] - (q[tt] - j) /w * v <= g[k] - (k - j)/w * v) tt--;
q[++tt] = k;
}
}
}
cout<<dp[V]<<endl;
return 0;
}
混合背包问题
- 题目:

-
分析:
再学完前面的三个后这个其实很简单,我们再输入时将多重背包二进制优化为01背包,保存标记为-1。这样最后遍历处理所有物品时就只有-1,0两种状态。分别用01背包和完全背包的滚动数组写法就可以了。
-
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
const int MA=1e3+5;
int dp[MA];
struct node
{
int kind;
int w,v;
};
vector<node> goods;
int main()
{
int n,V;
cin>>n>>V;
for(int i=0;i<n;++i){
int w,v,s;
cin>>w>>v>>s;
if(s<0)goods.push_back({-1,w,v});
else if(s==0) goods.push_back({0,w,v});
else{
for(int k=1;k<=s;k*=2){
s-=k;
goods.push_back({-1,w*k,v*k});
}
if(s>0)goods.push_back({-1,w*s,v*s});
}
}
for(auto good:goods){
if(good.kind==-1){
for(int j=V;j>=good.w;--j){
dp[j]=max(dp[j],dp[j-good.w]+good.v);
}
}
else{
for(int j=good.w;j<=V;++j){
dp[j]=max(dp[j],dp[j-good.w]+good.v);
}
}
}
cout<<dp[V]<<endl;
return 0;
}
二维费用的背包问题
- 题目:

-
分析:
其实和01背包很像,就是滚动数组时用二维操作。
-
代码:
#include<iostream> #include<cstdio> #include<cstring> #include<vector> #include<algorithm> using namespace std; typedef long long ll; const int MA=1e3+5; int dp[MA][MA]; int n,V,M; int main() { cin>>n>>V>>M; for(int i=0;i<n;++i){ int v,m,w; cin>>v>>m>>w; for(int j=V;j>=v;--j){ for(int k=M;k>=m;--k){ dp[j][k]=max(dp[j][k],dp[j-v][k-m]+w);//不选择和选择两种子问题 } } } cout<<dp[V][M]; return 0; }
分组背包问题
- 题目:

-
分析:
这是一个很大的问题,所以没有什么好的方法,直接三重循环。像所有背包问题一样,先循环物品,再循环容量,再循环决策。
-
代码:
#include<iostream> using namespace std; typedef long long ll; const int MA=1e3+5; int dp[MA],w[MA],v[MA]; int n,V,S; int main() { cin>>n>>V; for(int i=0;i<n;++i){ cin>>S; for(int j=0;j<S;++j)cin>>v[j]>>w[j]; for(int j=V;j>=0;--j){ for(int k=0;k<S;++k){ if(j>=v[k]) dp[j]=max(dp[j],dp[j-v[k]]+w[k]); } } } cout<<dp[V]<<endl; return 0; } -
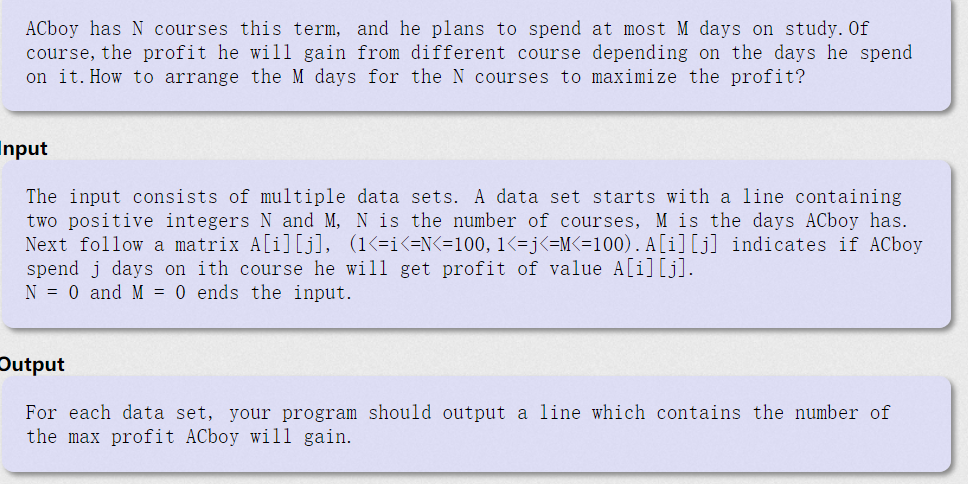
hdu1712
-
题意: N个课程,M天,之后一个N*M 的矩阵A[i ] [j], i 表示第 i 个课程,j 表示上这门课程的天数,A[i] [j] 表示上第i 门课程 j 天的收获。计算最大收获。
-
分析: 由于每一门课程只有一个选择天数,但有很多的选择,这些选择中(即上这门课程的天数)只能选择一个。很明显的分组背包问题,
-
代码:
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<vector> using namespace std; typedef long long ll; const int MA=1e2+5; int w[MA],v[MA]; int dp[MA]; int n,V; int main() { while(cin>>n>>V){//对每一组数据 if(n==0&&V==0)break; memset(dp,0,sizeof(dp));//多组数据一定要注意清零 for(int i=1;i<=n;++i){// n组 memset(w,0,sizeof(w)); for(int j=1;j<=V;++j){ //保存每一组v[j](这里v[j]=j所以省去),w[j] cin>>w[j]; } for(int j=V;j>=0;--j){ for(int k=1;k<=V;++k){ if(j>=k)dp[j]=max(dp[j],dp[j-k]+w[k]); } } } cout<<dp[V]<<endl; } return 0; }
有依赖的背包问题
-
代码:
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int N=1e3+5; int n,m; int e[N],ne[N],h[N],idx; int v[N],w[N]; int f[N][N]; void add(int x,int y)//x:父节点, y:子节点 { e[idx] = y, ne[idx] = h[x], h[x] = idx++; } void dfs(int x) { for(int i = h[x]; i != -1; i = ne[i]){ int y = e[i]; dfs(y); for(int j = m - v[x]; j >= 0; --j){ for(int k = 0; k <= j; ++k){ f[x][j] = max(f[x][j], f[x][j-k] + f[y][k]); } } } for(int i = m; i >= v[x]; --i){ f[x][i] = f[x][i - v[x]] + w[x]; } for(int i = 0; i < v[x]; ++i){ f[x][i] = 0; } } int main() { memset(h, -1,sizeof(h)); cin >> n >> m; int root; for(int i = 1; i <= n; ++i){ int p; cin >> v[i] >>w[i] >>p; if(p == -1){ root = i; } else { add(p,i); } } dfs(root); cout<<f[root][m]<<endl; return 0; }
背包问题求方案数
- 题目:

-
分析:
这道题是在01背包的基础上产生的,在01背包求最大价值的同时,用一个数组维护方案数。注意这里数组含义略有不同: f[ ]: 保存恰好等于各个容量时的最大价值,g[ ] : 保存恰好个容量时的方案数。
在更新f[ ]时,也更新一下方案数,这样就记录了方案数。因为题目要求最优选法的方案数,我们要先找到最优选法的最大价值,然后遍历所有价值,将价值等于最优价值的方案数相加,得到最终答案。
-
代码:
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int N=1010, mod = 1e9+7, INF = 1e7; int n,V; int f[N] ,g[N];//f: 保存恰好等于各个容量时的最大价值,g:保存恰好个容量时的方案数 int main() { cin>> n >> V; int v,w; for(int i=0;i<n;++i){ cin>> v >> w; for(int j = V; j >= v; --j){ int t = max(f[j], f[j-v] + w);//找到这两个间的最大值 int s=0; //s 用于保存方案数 if(t == f[j]) s += g[j]; if(t == f[j-v]+w) s +=g[j-v]; //这两步用于计算方案数,因为如果两个值相等,他们的方案数都应该统计。 if(s>=mod) s-=mod; f[j]=t; g[j]=s; } } int maxf=0; for(int j=0;j<=V;++j)maxf=max(maxf,f[j]); //找到所有容量下的最大价值 int res=0; //记录最终最大价值的方案数 for(int j=0;j<=V;++j){//遍历找到最大价值,加上他们对应的方案数 if(f[j]==maxf){ res+=g[j]; if(res>=mod)res-=mod; } } cout<<res<<endl; return 0; }
背包问题求具体方案
- 题目:

-
分析:
思路就是先求出最优价值,但不要用滚动数组,因为我们要用到各物品对应容量时的价值去判断这个物品是否被取。由于要按输出字典序最小的方案,我们在最后遍历判断每个物品是否被选时要从小到大判断。所以这也就要求我们在计算dp[] []时要从n往1 计算。
从n到1计算完dp[] []后,如果dp[i] [j] == dp[i +1] [j]说明没有选第 i 个物品,如果dp[i] [j] == dp[i+1] [j-v[i]]+w[i],说明第 i 个物品被选了。
-
代码:
#include<iostream> #include<cstring> #include<algorithm> using namespace std; const int N = 10100; int n,V; int w[N],v[N]; int dp[N][N]; int main() { cin>>n>>V; for(int i=1;i<=n;++i){ cin>>v[i]>>w[i]; } //dp数组 for(int i=n;i>=1;--i){ for(int j=0;j<=V;++j){ dp[i][j]=dp[i+1][j]; if(j>=v[i])dp[i][j]=max(dp[i][j], dp[i+1][j-v[i]] + w[i]); } } int vol = V; //从1到n遍历判断每个物品是否被选 for(int i=1;i<=n;++i){ //当遍历到第n个物品时,由于第n个物品不是由第n+1个物品转移来的。所以对第n个物品要特判。 if(i==n&&vol>=v[i]){//由于是最后一个,所以只要vol大于v[n]就说明选第n个了。 cout<<i<<' '; break; } //其他情况 if(vol>=v[i]&&dp[i][vol] == dp[i + 1][vol - v[i]] + w[i]){ cout<< i <<' '; vol -= v[i]; } if(vol < 0)break; } return 0; }
一些背包题目
cf189A
题意:输入n,a,b,c,让用a,b,c构成n,如何构成才能是abc使用数量最多。
分析:简直了一道裸完全背包(要装满)。如果会的话5minAC,,不会就暴力吧。。。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MA=1e5+5;
const int INF=1e9+5;
int dp[MA],a[5];
int main()
{
int V;
scanf("%d%d%d%d",&V,&a[1],&a[2],&a[3]);
for(int i=1;i<=V;++i)dp[i]=-INF;
for(int i=1;i<=3;++i){
for(int j=a[i];j<=V;++j){
dp[j]=max(dp[j],dp[j-a[i]]+1);
}
}
printf("%d
",dp[V]);
return 0;
}