Dijkstra算法
说明:求解从起点到任意点的最短距离,注意该算法应用于没有负边的图。
来,看图。
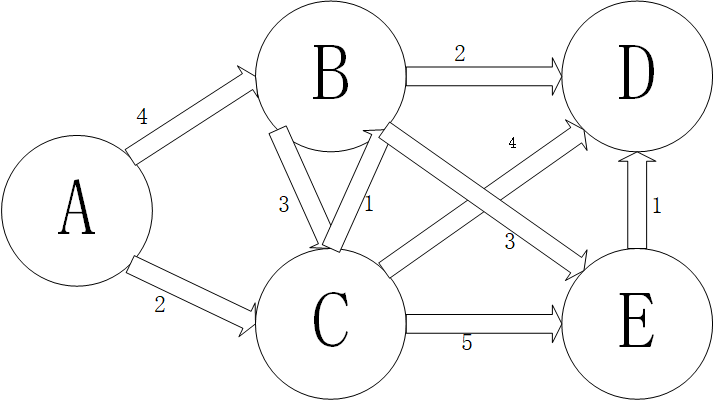
用邻接矩阵表示
int[][] m = {
{0, 0, 0, 0, 0, 0},
{0, 0, 4, 2, 0, 0},
{0, 0, 0, 3, 2, 3},
{0, 0, 1, 0, 4, 5},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0}};
备注:第一行(从第零行开始)表示A,第一列(从第零列开始)表示A。m[1][2]表示A到B的距离,如果没有相连则赋值为0。
首先用dist[i]数组表示从起点到该点的距离,比如dist[3]表示起点A到点C的距离。先全部初始化为无穷大,把起点初始化为0,因为自己到自己距离为0。接下来把所有的点的距离放入一个优先队列。步骤:
遍历直到队列为空:
在优先队列中删除值(dist[i])最小的点,不过记得保存下来,然后看与其相邻的点的距离,如果相邻的点的距离大于该点距离加上该点到相邻点的距离,则改变相邻的点的距离为该点距离加上该点到相邻点的距离,在优先队列中改变这个相邻的点的距离就好了。
解释:就是宽度优先搜索的变形,宽度优先搜索是直接从队列取出来就好了,没有优先顺序,而这个是根据该点的距离值(就是从起点到该点的距离)来确定优先出队顺序。
在这里优先队列实现的方案有四种:数组,二分堆,d堆,Fibonacci堆。复杂度可以自己去分析一下。提示:你可以计算从队列中删除和加入,复杂度分别是多少,就很容易算出来了。在这里说下数组的吧,从数组中删除最小的:o(V),插入:o(1),总:o(v^2)
来,看下我的代码实现。我是用的map,复杂度与数组实现类似。
import java.util.*; public class Main { public static int deleteMin(Map<Integer, Integer> map) { int min = Integer.MAX_VALUE; for (int num : map.values()) { min = Math.min(min, num); } int u = 0; for (int num : map.keySet()) { if (map.get(num) == min) { u = num; break; } } map.remove(u); return u; } public static void dijkstra(int[][] m) { int n = m.length; int[] dist = new int[n + 1]; int[] pre = new int[n + 1]; for (int i = 0; i < n; i++) dist[i] = Integer.MAX_VALUE; dist[1] = 0; pre[1] = 1; //点与距离 Map<Integer, Integer> map = new HashMap<>(); for (int i = 1; i < n; i++) { map.put(i, dist[i]); } while (!map.isEmpty()) { int u = deleteMin(map); for (int i = 1; i < n; i++) { if (m[u][i] > 0) { if (dist[i] > dist[u] + m[u][i]) { dist[i] = dist[u] + m[u][i]; pre[i] = u; map.put(i, dist[i]); } } } } for (int i = 1; i < n; i++) { System.out.println("节点1离节点" + i + "距离是:" + dist[i] + ",节点" + i +"的父节点是;" + pre[i]); } } public static void main(String[] args) { int[][] m = { {0, 0, 0, 0, 0, 0}, {0, 0, 4, 2, 0, 0}, {0, 0, 0, 3, 2, 3}, {0, 0, 1, 0, 4, 5}, {0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 1, 0}}; dijkstra(m); } }