【34.88%】【codeforces 569C】Primes or Palindromes?

time limit per test3 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
Rikhail Mubinchik believes that the current definition of prime numbers is obsolete as they are too complex and unpredictable. A palindromic number is another matter. It is aesthetically pleasing, and it has a number of remarkable properties. Help Rikhail to convince the scientific community in this!

Let us remind you that a number is called prime if it is integer larger than one, and is not divisible by any positive integer other than itself and one.

Rikhail calls a number a palindromic if it is integer, positive, and its decimal representation without leading zeros is a palindrome, i.e. reads the same from left to right and right to left.

One problem with prime numbers is that there are too many of them. Let’s introduce the following notation: π(n) — the number of primes no larger than n, rub(n) — the number of palindromic numbers no larger than n. Rikhail wants to prove that there are a lot more primes than palindromic ones.

He asked you to solve the following problem: for a given value of the coefficient A find the maximum n, such that π(n) ≤ A·rub(n).

Input
The input consists of two positive integers p, q, the numerator and denominator of the fraction that is the value of A (, ).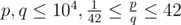

Output
If such maximum number exists, then print it. Otherwise, print “Palindromic tree is better than splay tree” (without the quotes).

Examples
input
1 1
output
40
input
1 42
output
1
input
6 4
output
172

【题目链接】:http://codeforces.com/contest/569/problem/C

【题解】

枚举n.最大枚举到150W就可以了;
这个150W的值是根据前n个数的质数/回文数的值来判断的;
当n>=120W左右时这个比值就达到了42;
真的是暴力出奇迹啊。。
判断的时候不能直接用比值。
两边同时乘个q再比较.不然精度不够的。

【完整代码】

#include <bits/stdc++.h>
using namespace std;
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define LL long long
#define rep1(i,a,b) for (int i = a;i <= b;i++)
#define rep2(i,a,b) for (int i = a;i >= b;i--)
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define rei(x) scanf("%d",&x)
#define rel(x) scanf("%I64d",&x)

typedef pair<int,int> pii;
typedef pair<LL,LL> pll;

//const int MAXN = x;
const int dx[9] = {0,1,-1,0,0,-1,-1,1,1};
const int dy[9] = {0,0,0,-1,1,-1,1,-1,1};
const double pi = acos(-1.0);
int p,q;
int pn,rubn;
double temp;

bool bo(string s,int l,int r)
{
    if (l >= r) return true;
    if (s[l]==s[r])
        return bo(s,l+1,r-1);
    else
        return false;
}

bool is_hui(LL x)
{
    string s = "";
    while (x>0)
    {
       s+= (x%10)+'0';
       x/=10;
    }
    return bo(s,0,s.size()-1);
}

bool is_zhi(LL x)
{
    if (x<2) return false;
    int ma = sqrt(x);
    rep1(i,2,ma)
        if ((x%i)==0)
            return false;
    return true;
}

int main()
{
    // freopen("F:\rush.txt","r",stdin);
    rei(p);rei(q);
    int ans;
    int i =1;
    while (i)
        {
            if (is_hui(i))
                rubn++;
            if (is_zhi(i))
                pn++;
            //double t = pn*1.0/rubn*1.0;
            //cout << t<<endl;
            if (q*pn<=p*rubn)
                ans = i;
            if (i>150e4) break;
            i++;
        }
    printf("%d
",ans);
    return 0;
}