题目出处:Find the median


示例:
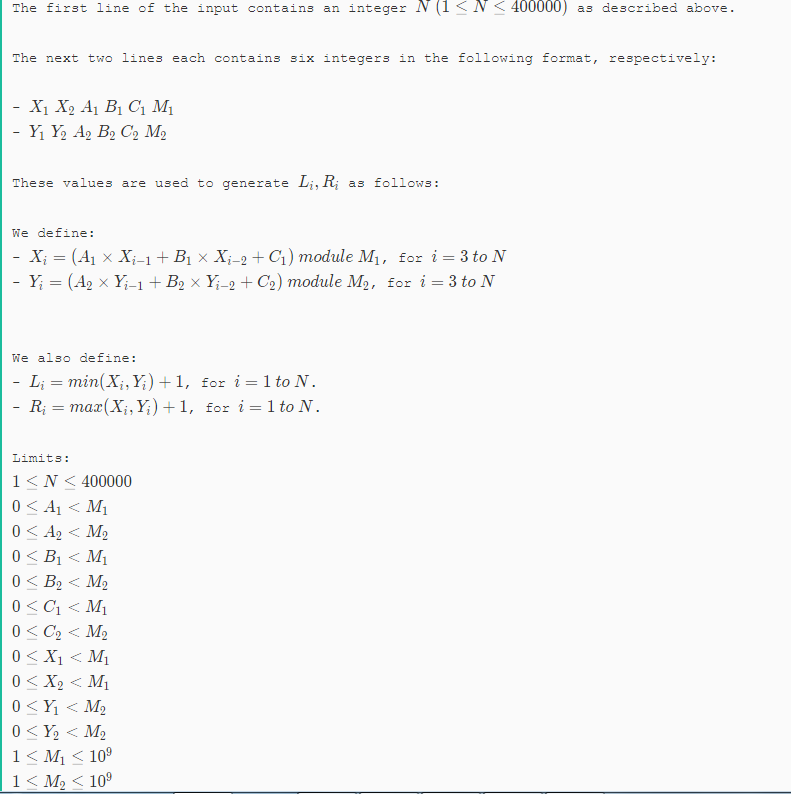
输入:
5
3 1 4 1 5 9
2 7 1 8 2 9
输出:3 4 5 4 5
说明:L = [3, 2 ,4, 1, 7],R = [4, 8, 8, 3, 9]
题意:每次插入[l[i],r[i]][l[i],r[i]],询问中位数
题解:线段树模版题+离散化(不懂或忘了这些的先补充下知识)。线段树的区间操作。但是由于范围太大,需要离散化,所以就出现了连续性的问题。所以只能用线段树维护 左闭右开 即:[w[l],w[r])。
code:
#include<bits/stdc++.h> #define LL long long using namespace std; const int maxx=8e6+200; LL summ[maxx],w[maxx],lz[maxx]; void pushdown(int l,int r,int root) { if(lz[root]){ int mid=(l+r)>>1; summ[root<<1]+=(w[mid]-w[l])*lz[root]; summ[root<<1|1]+=(w[r]-w[mid])*lz[root]; lz[root<<1]+=lz[root],lz[root<<1|1]+=lz[root]; lz[root]=0; } } void update(int l,int r,int root,int L,int R) { if(L<=l&&r-1<=R){//更新区间[w[l],w[r]] lz[root]++;//将一大段加入每个点加入的数储存,未用的不下放 summ[root]+=w[r]-w[l]; return ; } pushdown(l,r,root);//下放lz标记储存的数 int mid=(l+r)>>1; if(L<mid)update(l,mid,root<<1,L,R); if(R>=mid)update(mid,r,root<<1|1,L,R); summ[root]=summ[root<<1]+summ[root<<1|1]; } LL query(int l,int r,int root,LL k) { if(l+1==r){//当l+1=r时,表示当前最小的一段区间,该区间的数的个数一定相等 LL lo=summ[root]/(w[r]-w[l]); return w[l]+(k-1)/lo; } pushdown(l,r,root);//下发lz标记储存的数 int mid=(l+r)>>1; if(summ[root<<1]>=k)return query(l,mid,root<<1,k); else return query(mid,r,root<<1|1,k-summ[root<<1]); } LL n,tot=1,A1,A2,B1,B2,C1,C2,M1,M2; LL x[maxx],y[maxx],_l[maxx],_r[maxx]; int main() { scanf("%lld",&n); scanf("%lld%lld%lld%lld%lld%lld",&x[1],&x[2],&A1,&B1,&C1,&M1); scanf("%lld%lld%lld%lld%lld%lld",&y[1],&y[2],&A2,&B2,&C2,&M2); for(int i=3;i<=n;i++)//按题意算出xi、yi的值 x[i]=(A1*x[i-1]+B1*x[i-2]+C1)%M1,y[i]=(A2*y[i-1]+B2*y[i-2]+C2)%M2; for(int i=1;i<=n;i++){//按题意处理左右区域和储存所有点以便后面离散化 _l[i]=min(x[i],y[i])+1,_r[i]=max(x[i],y[i])+2;//为了得到一个较好的操作区间 w[tot++]=_l[i],w[tot++]=_r[i]; } sort(w+1,w+tot);//排序 tot=unique(w+1,w+tot)-w;//离散化去除重复点 LL sum=0;//统计第几次加入点后点的总数 for(int i=1;i<=n;i++){ int l=lower_bound(w+1,w+tot,_l[i])-w;// int r=lower_bound(w+1,w+tot,_r[i])-w; update(1,tot,1,l,r-1);//在线段树中加入一段新的数据 sum+=w[r]-w[l]; printf("%lld ",query(1,tot,1,(sum+1)/2));//查询第i段数据加入后的中位数 } return 0; }