MATLAB实现
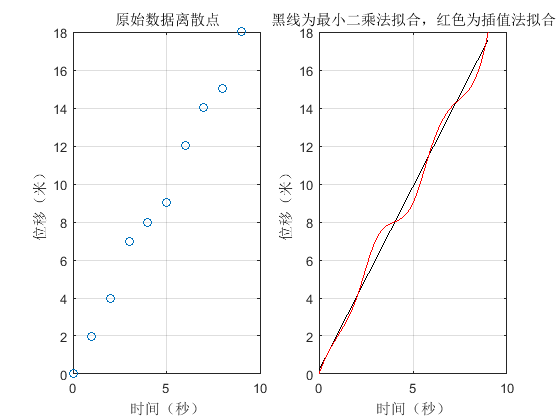
例一:时间与位移的关系
% 小车时间(xi)和位移关系(yi)关系 x = [0 1 2 3 4 5 6 7 8 9]; y = [0 2 4 7 8 9 12 14 15 18]; %{ subplot(m,n,p) 其中前两个参数 m,n是指将你的图分成 m*n个栅格, 每个栅格用 p 来编号,而编号是按行(横着)编号的,所以,当 m = 2,n = 2时编号规则为 1 | 2 ------ 3 | 4 所以subplot(2,2,[1 3]),就说明你这一个子图占据的是 1, 3两个栅格, 而subplot(2,2,2)说明子图仅占据第2个栅格. %} subplot(1,2,1); plot(x,y,'o'); % 图形的一些设置 xlabel('时间(秒)'); ylabel('位移(米)'); title('原始数据离散点') %{ grid on:是打开网格 grid off:是关闭网格 而grid是切换两种状态,如果在grid off的状态下,输入grid,相当于grid on 相反,如果在grid on状态下输入grid 等价于grid off %} grid on %{ polyfit函数是matlab中用于进行曲线拟合的一个函数。其数学基础是最小二乘法曲线拟合原理。 曲线拟合:已知离散点上的数据集,即已知在点集上的函数值,构造一个解析函数(其图形为一曲线)使在原离散点上尽可能接近给定的值。 调用方法:polyfit(x,y,n)。用多项式求过已知点的表达式, 其中x为源数据点对应的横坐标,可为行向量、矩阵; y为源数据点对应的纵坐标,可为行向量、矩阵; n为你要拟合的阶数,一阶直线拟合,二阶抛物线拟合,并非阶次越高越好,看拟合情况而定。 多项式在x处的值y可用下面程序计算:y=polyval(a,x,m) %} p = polyfit(x,y,1) % 0:0.01:9 起始为0,终点为9,步长0.01 x1 = 0:0.01:9; y1 = polyval(p,x1); x2 = 0:0.01:9; %{ MATLAB中的插值函数为interp1,其调用格式为: yi= interp1(x,y,xi,'method') 其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量, 'method'表示采用的插值方法,MATLAB提供的插值方法有几种: 'nearest'是最邻近插值, 'linear'线性插值; 'spline'三次样条插值; 'pchip'立方插值.缺省时表示线性插值 注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。 %} y2 = interp1(x,y,x2,'spline'); subplot(1,2,2); plot(x1,y1,'k',x2,y2,'r'); xlabel('时间(秒)'); ylabel('位移(米)'); title('黑线为最小二乘法拟合,红色为插值法拟合') grid on
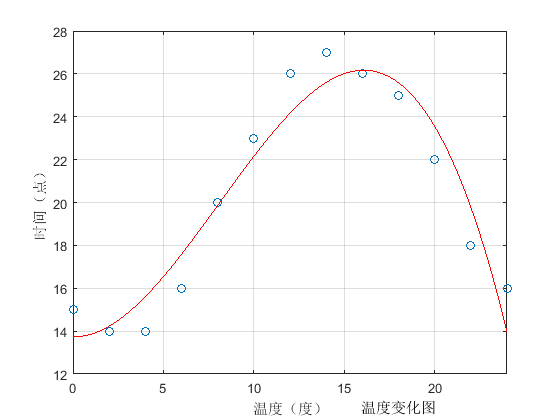
例二:温度与时间的关系
%{ 例如:对某日隔两小时测一次气温。设时间为ti,气温为Ci,i = 0,2 ,4,…,24。数据如下: 表2 温度(Ci)随时间(ti)变化关系 ----------------------------------------------------------- ti 0 2 4 6 8 10 12 14 16 18 20 22 24 ----------------------------------------------------------- ci 15 14 14 16 20 23 28 27 26 25 22 18 16 ----------------------------------------------------------- %} x = [0 2 4 6 8 10 12 14 16 18 20 22 24] y = [15 14 14 16 20 23 26 27 26 25 22 18 16] plot(x,y,'o') grid on %{ hold on 和hold off,是相对使用的 前者的意思是,你在当前图的轴(坐标系)中画了一幅图,再画另一幅图时,原来的图还在,与新图共存,都看得到 后者表达的是,你在当前图的轴(坐标系)中画了一幅图,此时,状态是hold off,则再画另一幅图时, 原来的图就看不到了,在轴上绘制的是新图,原图被替换了 %} hold on % 三阶拟合 得到的 p = -0.0061 0.1474 -0.0246 13.7390是个多项式的系数 % 即拟合的曲线y = -0.0061*x3 + 0.1474*x2 - 0.0246*x + 13.7390 (其中x3表示x的3次方,x2同理) p = polyfit(x,y,3) x1 = 0:0.01:24 y1 = polyval(p,x1) plot(x1,y1,'r') % axis坐标轴范围设置 axis([0 24 12 28]) xlabel('温度(度)'); ylabel('时间(点)'); title('温度变化图','position', [18,10])