链接 https://codeforces.com/problemset/problem/1284/E
题意:平面上有n个点,问你存在多少组四个点围成的四边形 严格包围某个点P的情况。不存在三点共线。
思路:首先看数据范围是2500,可以做n^2的枚举,我们可以枚举两遍n。正面求解有些困难,反面求解可以考虑有多少组子集不满足题目要求,拿总的子集数量减去不满足的就是答案。
那么考虑不满足题意的点集。
首先如果对于一对点P和P1,让它们连线,以P为基准,相对度数为0度,枚举P和P1这个条线以上的所有点,假设枚举出n个点,n个点加P1,从中选出4个点,这4个点组成的四边形必定不含点P,以此性质
首先做一遍极角排序,然后固定一条边,以这条边为0度,开始扫描这条边0到180度的所有点,然后从中任意选出3个点C(n,3),与P1组成的四边形便不封闭包围P1,统计所有不满足条件的点集,用总体点集
个数C(n,5)- 不满足的组合个数 就是答案了。
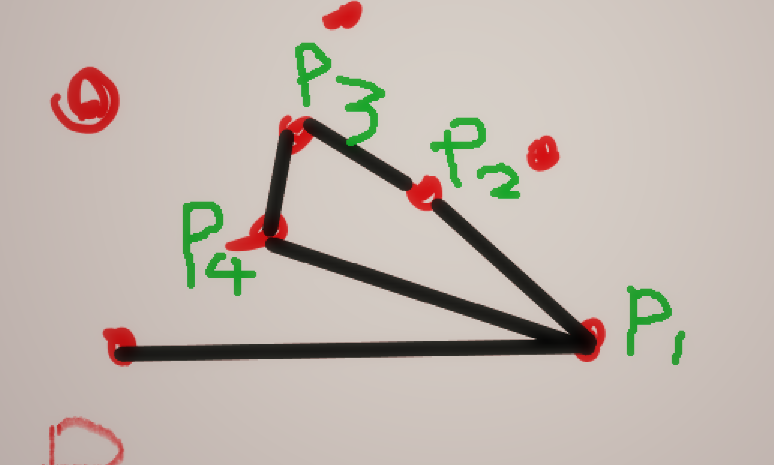
(如图所示,P1,P2,P3,P4组成的四边形不封闭包围点P。)
AC代码:
1 #include<iostream> 2 #include<vector> 3 #include<cstdlib> 4 #include<cstdio> 5 #include<algorithm> 6 #include<cmath> 7 #include<cstring> 8 #include<queue> 9 #include<map> 10 using namespace std; 11 typedef long long ll; 12 const long double pi = acos(-1.0L); 13 const int maxn = 2e3+600; 14 long double x[maxn],y[maxn]; 15 int main() 16 { 17 int n;cin>>n; 18 ll ans = (ll)n*(n-1)*(n-2)*(n-3)*(n-4)/24; 19 for(int i = 0;i<n;i++){ 20 ll xi,yi; 21 cin>>xi>>yi; 22 x[i] = xi,y[i] = yi; 23 } 24 for(int i = 0;i<n;i++){ 25 vector<long double> v; 26 for(int j = 0;j<n;j++){ 27 if(i == j) continue; 28 v.push_back(atan2(y[j]-y[i],x[j]-x[i])); //算一下角度 29 } 30 sort(v.begin(),v.end());//做极角排序 31 int k = n - 1 , cur = 0; 32 for(int j = 0;j<k;j++){ 33 while(cur < j+k){ //枚举点个数增加一倍 34 long double angle = v[cur%k] - v[j];//枚举两条边的夹角 35 if(angle < 0) angle+=2*pi;//如果角度小于0,则增加2*pi转一圈 36 if(angle < pi) cur++;//如果该点在枚举的这条线上面,则cur++ 37 else break; 38 } 39 long long cnt = cur - j - 1; 40 ans-=1ll*cnt*(cnt-1)*(cnt-2)/6; 41 } 42 } 43 cout<<ans; 44 return 0; 45 }