POJ 3041 Asteroids（二分图最大匹配）

###题目链接###

题目大意：

给你 N 和 K ，在一个 N * N 个图上有 K 个 小行星。有一个可以横着切或竖着切的武器，问最少切多少次，所有行星都会被毁灭。

分析：

将 1~n 行数加入左集合，将 1~n 列数加入右集合。然后将所给的所有点当成无向边，在二分图上连接。

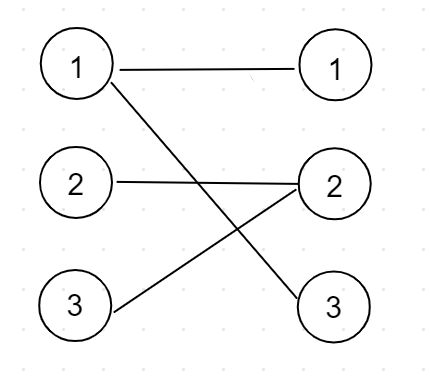
1、对于每条边，只要有其中一个端点被选取，则该条边所代表的行星就可以被摧毁。同样，如果选取了这个端点，则所有与这个端点连接的所有行星都会被一次摧毁。

2、对于样例，假设我选取了 1（左集合）--- 1（右集合） 这条边，则说明我已经选择了 横着切第一行 或者 竖着切第一列 。那么与 1（左集合） 所连接的所有边代表的小行星都会被消除，对于 1（右集合） 同理。

故发现：已选取的边所对应两端点 A 和 B，则 A 有关其他边 与 B 有关的其他边不需要被选取了，且 A 和 B 点不需要再被选取。

所以这题的本质是一道 最小点覆盖数问题。

最小覆盖问题：求最少个数的点，使得图中所有边都能有至少一个端点已被选取。意思是选取了一个点，那么以该点为端点的边都会被覆盖。

那么二分图最小覆盖 等价于 二分图最大匹配。 

#include<iostream>
#include<algorithm>
#include<string.h>
#define maxn 1008
using namespace std;
int n,m,e,cnt;
int head[maxn];
int cx[maxn],cy[maxn];
bool vis[maxn];
struct Edge
{
    int to;
    int next;
}edge[maxn*maxn];
inline void add(int u,int v)
{
    edge[++cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt;
    return;
}
inline int dfs(int u)
{
    for(int i=head[u];i;i=edge[i].next){
        int v=edge[i].to;
        if(!vis[v]){
            vis[v]=true;
            if(cy[v]==0||dfs(cy[v])){
                cx[u]=v;
                cy[v]=u;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    // =freopen("testdata (7).in","r",stdin);
    scanf("%d%d",&n,&m);
    int A,B;
    for(int i=1;i<=m;i++){scanf("%d%d",&A,&B);add(A,B);}
    int ans = 0;
    for(int i=1;i<=n;i++){
        if(!cx[i]) {memset(vis,0,sizeof(vis)); ans += dfs(i);}
    }
    printf("%d
",ans );
}