中国剩余定理（CRT）

只看懂了CRT，EXCRT待补。。。。

心得：记不得这是第几次翻CRT了，每次都有迷迷糊糊的。。

中国剩余定理用来求解类似这样的方程组：

　　　　　　　　

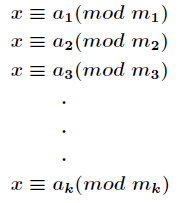
求解的过程中用到了同余方程。

x=a1( mod x1)

x=a2( mod x2)

x=a3( mod x3)

假设：

n1=a1( mod x1)

n2=a2( mod x2)

n3=a3( mod x3)
已知n1满足除以3余2，能不能使得n1+n2的和仍然满足%x1=a1？

所以n2应该是x2的倍数，其余同理。

所以当答案为n1+n2+n3时，n1应该是a2和a3的倍数，n2应该是a1和a3的倍数，n3应该是a1和a2的倍数。

所以这个问题的答案就可以转换为从a2和a3的LCM种找到满足%x1=a1的n1，（n2,n3同理）

数学上有一个定理：若x%c=b，则x/2 % c= b/2， 同理(x*k)%c=(b*k)%c。

假设c1=lcm(x2,x3)，c1*(c1的逆元)=1 ( mod ) x1。然后两边同时乘a1就是a1*c1*(c1的逆元)=a1(mod x1).

所以n1=a1*c1*(c1关于x1的逆元)

n2的求法类似.然后累加就好了。

code:

void exgcd(ll a,ll b,ll &x,ll &y){
    if(b==0) {
        x=1;y=0;
    }
    else {
        exgcd(b,a%b,y,x);
        y-=(a/b)*x;
    }
}
ll china(int a[],int m[],int n){//m是余数数组，a是模数数组，n是等式的个数
    ll M=1,x,y;
    ll ans=0;
    for(ll i=1;i<=n;i++) M*=a[i];
    for(ll i=1;i<=n;i++){
        ll w=M/a[i];
        exgcd(w,a[i],x,y);
        ans=(ans+m[i]*w*x)%M;
    }
    return (ans+M)%M;
}