1 什么是差分约束系统
设有一组不等式:

不等式的特点是 xi-xj<=Ck.(当然大于等于也可以,因为乘以个-1就可以变换,单纯的小于的话,要让Ck-1转换为小于等于),我们把这样的不等式组成为差分约束。
这个不等式组要么有无穷多解,要么无解。假设存在一组解{x1,x2,x3,x4,x5},那么{x1+k,x2+k,x3+k,x4+k,x5+k}同样也是该方程组的一组解。
2 差分约束系统的解
差分约束系统的解常常与最短路算法联系在一起
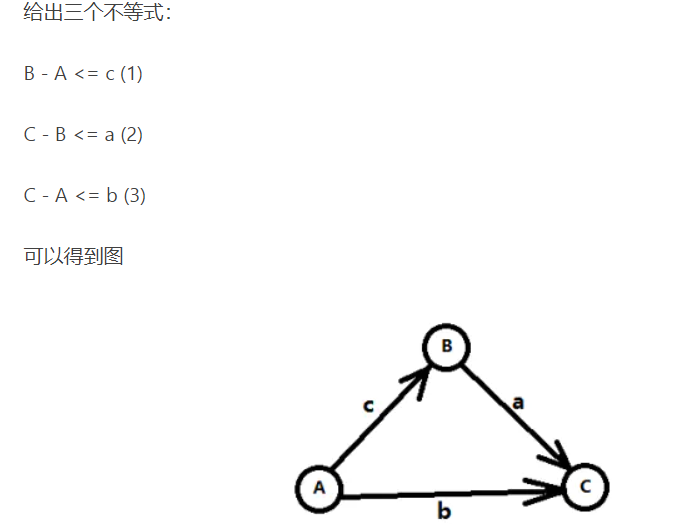
看一下这个图,从A->B有一条距离为C的边......。然后我们求从A到C的距离dis[c]=min(b,a+c),然后再看一下上面的三个不等式,C-A<=b并且C-A<=a+c(不等式1和不等式2相加)
这个过程和最短路算法里的松弛过程特别类似。
3 构图
根据上图,假设有不等式B-A<=C,就会有一条A到B的边,权值为C,与之对应。所有根据不等式我们可以构造出与之对应的边来。什么情况下无解?不等式无解映射到最短路中也就是当出现负权环的时候(最长路是正权环时无解)。
4 增加超级源点
具体实现时,往往在原图上附加一个顶点,这个顶点与每个顶点都连接一条权值为0的边,以上述不等式为例,也就是新加入一个未知的不等式组
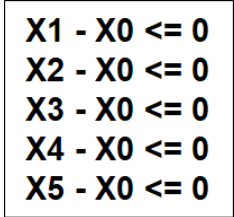
然后以x0为起点跑SPFA,求得的dis[i]就是xi的最大值了。一个无形的条件dis[x0]=0,也就是说我们把x0当做源点,x0到x0的距离当然为0,如果我们修改dis[x0]=A,扎样的话我们就可以限制每个xi的范围了,每个xi就小于等于A。。。
https://blog.csdn.net/dragon60066/article/details/80245797