网络流初识三--（dinic算法）

dicnic算法求最大流。

dicnic算法就像是对F-F算法的一个优化，F-F算法是无脑求增广路径，直到求不出来路径为止。

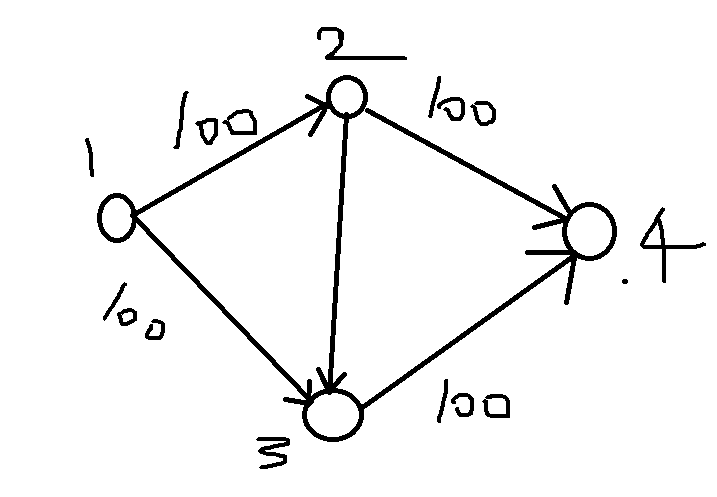
 比如说这个图，求从1~4的最大流量，很显然应该是200，路径1--2--4和路径1--3--4。但是如果FF算法第一次走的路径是1--2--3--4，那么这条路径的流量就变成了1，然后根据FF算法的步骤，下一步建反向边再跑图，比如说走的是1--3--2--4

然后再建返向边再跑。。。。一直把1--2和1--3这两条边的流量跑完为止。这样算法的性能一下就下去了，而dicnic算法刚好解决了这个问题。

首先对残余网络进行分层，用一个数组dis记录一下，比如说dis[]...dis[1]=0，dis[2]=dis[3]=1，dis[4]=2。在dfs寻找增广路的时候，只能一层接着一层的寻找，可以想象成一个楼梯，源点在最低层，汇点在最高层，从最底层向最高层走，那么相同层之间走就没有了什么意义了。

简而言之，dicnic算法就是先对当前网络进行分层，然后再从分层的基础上寻找增广路径，直到找不到增广路径，再更新网络分层

记一个洛谷的简单的板子题。

code:

#include<bits/stdc++.h>
using namespace std;
const int N=120000+120000+7;
const long long  INF=1e18+7;
class stu{
    public:
        int to,nxt;
        long long val;
}edge[N];
int n,m,s,t;
int flag[1200+1][1200+1];
long long  dis[N];
int tol=0;
int head[N];
void add(int x,int y,long long  z){
    edge[tol].to=y;
    edge[tol].val=z;
    edge[tol].nxt=head[x];
    head[x]=tol++;
}
bool bfs(int s,int t){
    for(int i=0;i<=n;i++) dis[i]=INF;
    queue<int>que;
    dis[s]=0;
    que.push(s);
    while(!que.empty()){
        int u=que.front();
        que.pop();
        for(int i=head[u];i!=-1;i=edge[i].nxt){
            int v=edge[i].to;
            long long w=edge[i].val;
            if(w>0&&dis[u]+1<dis[v]) {
                dis[v]=dis[u]+1;
                que.push(v);
            }
        }
    }
    return dis[t]!=INF;
}
int dfs(int s,int t,long long  mn){
    if(s==t) return mn;
    for(int i=head[s];i!=-1;i=edge[i].nxt){
        int v=edge[i].to;
        long long w=edge[i].val;
        if(w<=0||dis[v]!=dis[s]+1) continue ;
        int cw=dfs(v,t,min(w,mn));
        if(cw>0){
            edge[i].val-=cw;
            edge[i^1].val+=cw;
            return cw;
        }
    }
    return 0;
}
void dicnic(int s,int t){
    long long  ans=0;
    while(bfs(s,t)){
        int d;
        while(d=dfs(s,t,INF)){
            ans+=d;
        }
    }
    printf("%lld",ans);
}
     
int main(){
    memset(head,-1,sizeof head); 
    scanf("%d%d%d%d",&n,&m,&s,&t);
    int x,y;
    long long z;
    for(int i=1;i<=m;i++){
        scanf("%d%d%lld",&x,&y,&z);
        if(!flag[x][y]){
            add(x,y,z);
            flag[x][y]=tol;
            add(y,x,0);
        }
        else  edge[flag[x][y]-1].val+=z;
    }
    dicnic(s,t);
    return 0;
} 

 dinic算法的当前弧优化：

　　当前弧优化是在dfs寻找增广路径的时候加的一个优化。假如说某一个点s个3个子节点，那么就对应3条有向边，编号分别为1,2,3。在dfs的寻路的过程按顺序依次遍历1,2,3，假如说从第一次找到的从S---T的路径为从二号边往下的路径，即1号边不能到达T，这时我们就记录一下2号边，当再次寻路的时候直接从2号边开始寻找就行了，没必要再找一遍1号边了。这种优化成为当前弧优化。

实现起来也比较简单：

#include<bits/stdc++.h>
using namespace std;
const int N=120000+120000+7;
const long long  INF=1e18+7;
int cur[N];
class stu{
    public:
        int to,nxt;
        long long val;
}edge[N];
int n,m,s,t;
int flag[1200+1][1200+1];
long long  dis[N];
int tol=0;
int head[N];
void add(int x,int y,long long  z){
    edge[tol].to=y;
    edge[tol].val=z;
    edge[tol].nxt=head[x];
    head[x]=tol++;
}
bool bfs(int s,int t){
    for(int i=0;i<=n;i++) dis[i]=INF;
    queue<int>que;
    dis[s]=0;
    que.push(s);
    while(!que.empty()){
        int u=que.front();
        que.pop();
        for(int i=head[u];i!=-1;i=edge[i].nxt){
            int v=edge[i].to;
            long long w=edge[i].val;
            if(w>0&&dis[u]+1<dis[v]) {
                dis[v]=dis[u]+1;
                que.push(v);
                if(v==t) return dis[t]!=INF;
            }
        }
    }
    return dis[t]!=INF;
}
int dfs(int s,int t,long long  mn){
    if(s==t) return mn;
    for(int i=cur[s];i!=-1;i=edge[i].nxt){
        cur[s]=i;
        int v=edge[i].to;
        long long w=edge[i].val;
        if(w<=0||dis[v]!=dis[s]+1) continue ;
        int cw=dfs(v,t,min(w,mn));
        if(cw>0){
            edge[i].val-=cw;
            edge[i^1].val+=cw;
            return cw;
        }
    }
    return 0;
}
void dicnic(int s,int t){
    long long  ans=0;
    while(bfs(s,t)){
        for(int i=1;i<=n;i++){
            cur[i]=head[i];
        }
        int d;
        while(d=dfs(s,t,INF)){
            ans+=d;
        }
    }
    printf("%lld",ans);
}
int main(){
    memset(head,-1,sizeof head); 
    scanf("%d%d%d%d",&n,&m,&s,&t);
    int x,y;
    long long z;
    for(int i=1;i<=m;i++){
        scanf("%d%d%lld",&x,&y,&z);
        if(!flag[x][y]){
            add(x,y,z);
            flag[x][y]=tol;
            add(y,x,0);
        }
        else  edge[flag[x][y]-1].val+=z;
    }
    dicnic(s,t);
    return 0;
}