LiMn2O4的数学之路

题面：

长期以来，LiMn2O4常常会因为自己成为不了数学选手而苦恼，并曾经有过一次转型的尝试。那是一个月黑风高的十一长假，LiMn2O4拿起了厚厚的《具体数学》。路过的practer看见了，practer说你有没有办法求一下这个公式的值：

LiMn2O4看了眼公式，说这个值有无理数，怎么表示？可以做？于是practer给了LiMn2O4第另一个公式：

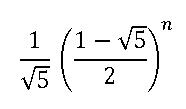
求第一个公式减第二个公式的值。LiMn2O4稍加思考后觉得这个太简单了，他还要看《具体数学》，没有时间。现在交给聪明的你来解决这个问题，请你求出新的公式的第N项。

思路：

斐波那契通项公式

矩阵快速幂

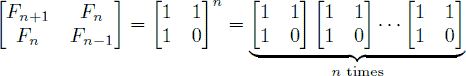
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll p=1000000007;
struct node{
    ll a[2][2];
    node()
    {
        memset(a,0,sizeof(a));
    }
};
node mul(node a,node b)
{
    node s;
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
            for(int k=0;k<2;k++)
                s.a[i][k]=(s.a[i][k]+a.a[i][j]*b.a[j][k])%p;
    return s;
}
node pow(node a,ll n)
{
    node s;
    for(int i=0;i<2;i++)
        s.a[i][i]=1;
    while(n)
    {
        if(n&1)
            s=mul(s,a);
        a=mul(a,a);
        n>>=1;
    }
    return s;
}
ll n,x;
int main()
{
    node a;
    scanf("%lld
",&n);
    a.a[0][0]=a.a[1][0]=a.a[0][1]=1;
    for (int i=1;i<=n;i++)
    {
        scanf("%lld",&x);
        node s=pow(a,x);
        cout<<s.a[1][0]<<endl;
    }
    return 0;
}