http://acm.hdu.edu.cn/showproblem.php?pid=6604
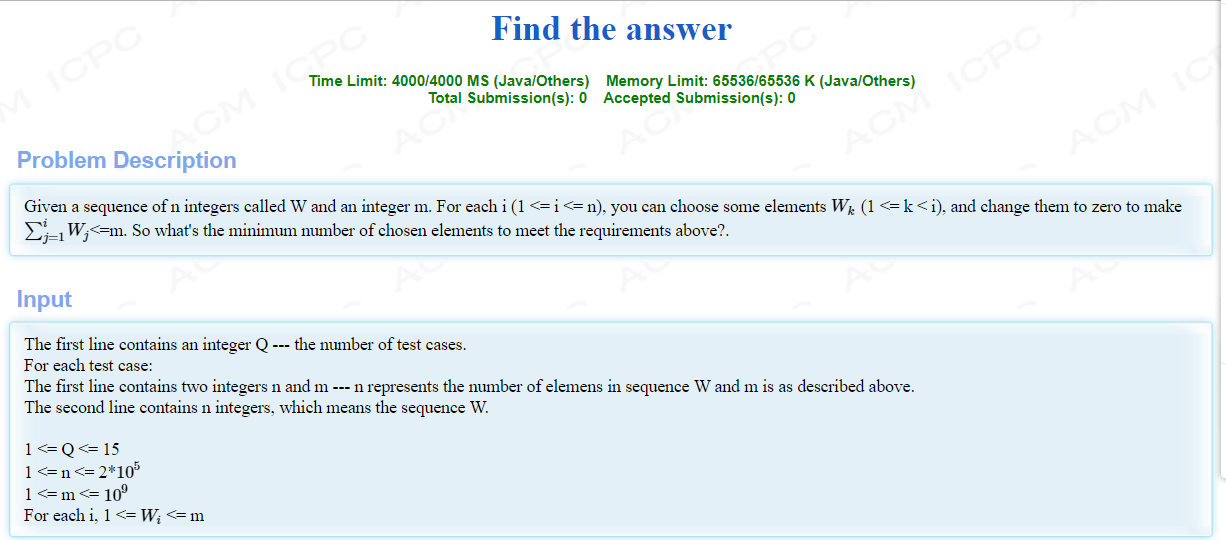
Problem Description
Country A and B are at war. Country A needs to organize transport teams to deliver supplies toward some command center cities.
In order to ensure the delivery works efficiently, all the roads in country A work only one direction. Therefore, map of country A can be regarded as DAG( Directed Acyclic Graph ). Command center cities only received supplies and not send out supplies.
Intelligence agency of country B is credibly informed that there will be two cities carrying out a critical transporting task in country A.
As long as **any** one of the two cities can not reach a command center city, the mission fails and country B will hold an enormous advantage. Therefore, country B plans to destroy one of the n cities in country A and all the roads directly connected. (If a city carrying out the task is also a command center city, it is possible to destroy the city to make the mission fail)
Now country B has made q hypotheses about the two cities carrying out the critical task.
Calculate the number of plan that makes the mission of country A fail.Input
The first line contains a integer T (1≤T≤10), denoting the number of test cases.
In each test case, the first line are two integers n,m, denoting the number of cities and roads(1≤n≤100,000,1≤m≤200,000).
Then m lines follow, each with two integers u and v, which means there is a directed road from city u to v (1≤u,v≤n,u≠v).
The next line is a integer q, denoting the number of queries (1≤q≤100,000)
And then q lines follow, each with two integers a and b, which means the two cities carrying out the critical task are a and b (1≤a,b≤n,a≠b).
A city is a command center if and only if there is no road from it (its out degree is zero).Output
For each query output a line with one integer, means the number of plan that makes the mission of country A fail.Sample Input
2 8 8 1 2 3 4 3 5 4 6 4 7 5 7 6 8 7 8 2 1 3 6 7 3 2 3 1 3 2 2 1 2 3 1Sample Output
4 3 2 2
#include <bits/stdc++.h> using namespace std; const int maxn=2e5+10; int n,m,tim,dfn[maxn],repos[maxn],idom[maxn],fa[maxn],mi[maxn],f[maxn],semi[maxn],id[maxn],ans[maxn]; int d[maxn],lc[maxn][25],w[maxn],T=24; struct edge { int tot, head[maxn], next[maxn], to[maxn]; void clear() { tot = 0; for (int i = 0; i <= n; i++) head[i] = 0; } void add(int u, int v) { to[++tot] = v; next[tot] = head[u]; head[u] = tot; } }G,RG,NG,TR; void init(){ tim=0; G.clear();RG.clear();NG.clear();TR.clear(); memset(lc,0, sizeof(lc)); for (int i=1;i<=n;i++){ repos[i]=dfn[i]=idom[i]=fa[i]=ans[i]=0; mi[i]=semi[i]=f[i]=i; w[i]=0; } } void dfs1(int x) { dfn[x] = ++tim; repos[tim] = x; for (int i = G.head[x]; i; i = G.next[i]) if (!dfn[G.to[i]]) { fa[G.to[i]] = x; dfs1(G.to[i]); } } int find(int x) { if (x == f[x]) return x; int tmp = f[x]; f[x] = find(f[x]); if (dfn[semi[mi[tmp]]] < dfn[semi[mi[x]]]) mi[x] = mi[tmp]; return f[x]; } void dfs(int x) { for (int i = TR.head[x]; i; i = TR.next[i]) { int to = TR.to[i]; d[to] = d[x] + 1; lc[to][0] = x; ans[to] += ans[x] + 1;//记录虚点到该点的支配点个数 for (int j = 1;j<=T; j++) lc[to][j] = lc[lc[to][j - 1]][j - 1]; dfs(to); } } int lca(int x,int y) { if (d[x] > d[y]) swap(x, y); for (int i = T; i >= 0; i--) { if (d[lc[y][i]] >= d[x]) y = lc[y][i]; } if (x == y) return x; for (int i = T; i >= 0; i--) { if (lc[x][i] != lc[y][i]) { x = lc[x][i]; y = lc[y][i]; } } return lc[x][0]; } void work() { for (int i = n; i >= 2; i--) { int x = repos[i], tmp = n; for (int j = RG.head[x]; j; j = RG.next[j]) { if (!dfn[RG.to[j]]) continue; if (dfn[RG.to[j]] < dfn[x]) tmp = min(tmp, dfn[RG.to[j]]); else { find(RG.to[j]); tmp = min(tmp, dfn[semi[mi[RG.to[j]]]]); } } semi[x] = repos[tmp]; f[x] = fa[x]; NG.add(semi[x], x); x = repos[i - 1]; for (int j = NG.head[x]; j; j = NG.next[j]) { int y = NG.to[j]; find(y); if (semi[mi[y]] == semi[y]) idom[y] = semi[y]; else idom[y] = mi[y]; } } for (int i = 2; i <= n; i++) { int x = repos[i]; if (idom[x] != semi[x]) idom[x] = idom[idom[x]]; TR.add(idom[x], x); } d[1]=1; dfs(1); } int main() { int _; scanf("%d", &_); while (_--) { scanf("%d%d", &n, &m); n++; init(); for (int i = 1, v, u; i <= m; i++) { scanf("%d%d",&u, &v); u++;v++; swap(u, v); w[v]++; G.add(u, v); RG.add(v, u); } for (int i = 2; i <= n; i++) { if (!w[i]) { G.add(1,i); RG.add(i,1); } } dfs1(1); work(); int q, x, y; scanf("%d", &q); while (q--) { scanf("%d%d", &x, &y); x++; y++; printf("%d ", ans[x] + ans[y] - ans[lca(x, y)]); } } return 0; }


#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int S=8;
ll mult_mod(ll a,ll b,ll c)
{
a%=c;
b%=c;
ll ret=0,tmp=a;
while (b)
{
if (b&1)
{
ret+=tmp;
if (ret>c)
{
ret-=c;
}
}
tmp<<=1;
if (tmp>c) tmp-=c;
b>>=1;
}
return ret;
}
ll pow_mod(ll a,ll n,ll mod)
{
ll ret=1;
ll temp=a%mod;
while (n)
{
if(n&1)
{
ret=mult_mod(ret,temp,mod);
}
temp=mult_mod(temp,temp,mod);
n>>=1;
}
return ret;
}
bool check(ll a,ll n,ll x,ll t)
{
ll ret=pow_mod(a,x,n);
ll last=ret;
for (int i=1; i<=t; i++)
{
ret=mult_mod(ret,ret,n);
if (ret==1&&last!=1&&last!=n-1)
{
return 1;
}
last=ret;
}
if (ret!=1)
{
return 1;
}
return 0;
}
bool Miller_Rabin(ll n)
{
if (n<2)
{
return 0;
}
if (n==2)
{
return 1;
}
if ((n&1)==0)
{
return 0;
}
ll x=n-1;
ll t=0;
while ((x&1)==0)
{
x>>=1;
t++;
}
srand(time(NULL));
for (int i=0; i<S; i++)
{
ll a=rand()%(n-1)+1;
if (check(a,n,x,t))
{
return 0;
}
}
return 1;
}
ll factor[100];
int tol;
ll gcd(ll a,ll b)
{
if (!b)
{
return a;
}
return gcd(b,a%b);
}
ll pollard_rho(ll x,ll c)
{
ll i=1,k=2;
srand(time(NULL));
ll x0=rand()%(x-1)+1;
ll y=x0;
while (1)
{
i++;
x0=(mult_mod(x0,x0,x)+c)%x;
ll d=gcd(y-x0,x);
if (d!=1&&d!=x)
{
return d;
}
if (y==x0)
{
return x;
}
if (i==k)
{
y=x0;
k+=k;
}
}
}
__int128 quick(__int128 a,__int128 b,__int128 p)
{
__int128 ret=1%p;
while (b)
{
if (b&1)
{
ret=ret*a%p;
}
b>>=1;
a=a*a%p;
}
return ret;
}
void findfac(ll n,ll k)
{
if (n==1)
{
return;
}
if (Miller_Rabin(n))
{
factor[tol++]=n;
return;
}
ll p=n;
ll c=k;
while (p>=n)
{
p=pollard_rho(p,c--);
}
findfac(p,k);
findfac(n/p,k);
}
__int128 inv(__int128 a,__int128 p){
return quick(a,p-2,p);
}
int main()
{
ll t,p,prime;
__int128 ans;
scanf("%lld",&t);
while (t--)
{
scanf("%lld",&p);
for (ll i=p-1; i>=2; i--)
{
if (Miller_Rabin(i))
{
prime=i;
break;
}
}
ans=p-1;
for (__int128 i=p-1;i>prime;i--){
ans=ans*inv(i,p)%p;
}
printf("%lld
",(ll)ans);
}
}

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=200010;
ll w[N],b[N],n,m;
struct node{
ll num,sum;
}t[N*4];
struct data{
ll num,rk,id;
}a[N];
inline void build(ll rt,ll l,ll r) {
t[rt].num = t[rt].sum = 0;
if (l == r) {
return;
}
ll mid = (l + r) >> 1;
build(rt << 1, l, mid);
build(rt << 1 | 1, mid + 1, r);
}
inline void change(ll rt,ll pos,ll l,ll r) {
if (l == r) {
t[rt].num = 1;
t[rt].sum = b[pos];
return;
}
ll mid = (l + r) >> 1;
if (pos <= mid) {
change(rt << 1, pos, l, mid);
} else {
change(rt << 1 | 1, pos, mid + 1, r);
}
t[rt].sum = t[rt << 1].sum + t[rt << 1 | 1].sum;
t[rt].num = t[rt << 1].num + t[rt << 1 | 1].num;
}
inline ll query(ll rt,ll w,ll l,ll r) {
if (l == r) {
return t[rt].sum <= w ? t[rt].num : 0;
}
ll mid=(l+r)>>1;
if (t[rt << 1].sum <= w) {
return t[rt << 1].num + query(rt << 1 | 1, w - t[rt << 1].sum,mid+1,r);
} else {
return query(rt << 1, w, l, mid);
}
}
inline bool cmp1(data a,data b) {
return a.num < b.num;
}
inline bool cmp2(data a,data b) {
return a.id < b.id;
}
int main() {
int t;
scanf("%d", &t);
while (t--) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%lld", &w[i]);
a[i].id = i;
a[i].num = w[i];
}
sort(a + 1, a + n + 1, cmp1);
for (int i = 1; i <= n; i++) {
a[i].rk = i;
b[i] = a[i].num;
}
sort(a + 1, a + n + 1, cmp2);
build(1, 1, n);
for (int i = 1; i <= n; i++) {
printf("%lld ", i - query(1, m - w[i], 1, n) - 1);
change(1, a[i].rk, 1, n);
}
printf("
");
}
}

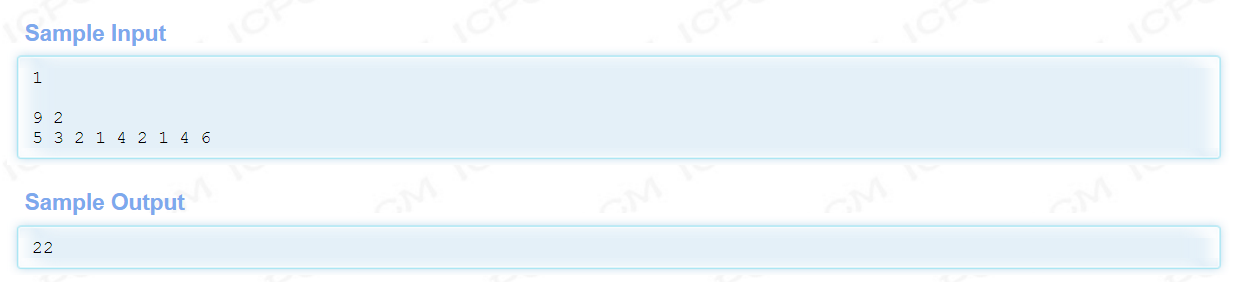

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PI;
const int maxn=5000;
const int inf=0x3f3f3f3f;
int a[maxn];
struct Min_Cost_Max_Flow{
struct edge{
int to,cap,cost,rev;
edge(){};
edge(int _to,int _cap,int _cost,int _rev):to(_to),cap(_cap),cost(_cost),rev(_rev){};
};
vector<edge>E[maxn];
int h[maxn],n,d[maxn],preV[maxn],preE[maxn];
void init(int n){
this->n=n;
for (int i=0;i<=n;i++){
E[i].clear();
h[i]=0;
}
}
void add(int from,int to,int cap,int cost){
E[from].push_back(edge(to,cap,cost,E[to].size()));
E[to].push_back(edge(from,0,-cost,E[from].size()-1));
}
PI dijkstra(int s,int t,int f){
int cost=0,flow=0;
for (int i=0;i<=n;i++){
h[i]=0;
}
while (f){
priority_queue<PI,vector<PI>,greater<PI> >q;
for (int i=0;i<=n;i++){
d[i]=inf;
}
d[s]=0;
q.push(make_pair(0,s));
while (!q.empty()){
PI now=q.top();
q.pop();
int v=now.second;
if (d[v]<now.first){
continue;
}
for (int i=0;i<E[v].size();i++){
edge &e=E[v][i];
if (e.cap>0&&d[e.to]>d[v]+e.cost+h[v]-h[e.to]){
d[e.to]=d[v]+e.cost+h[v]-h[e.to];
preV[e.to]=v;
preE[e.to]=i;
q.push(make_pair(d[e.to],e.to));
}
}
}
if (d[t]==inf)break;
for (int i=0;i<=n;i++){
h[i]+=d[i];
}
int d=f;
for (int i=t;i!=s;i=preV[i]){
d=min(d,E[preV[i]][preE[i]].cap);
}
f-=d;
flow+=d;
cost+=d*h[t];
for (int i=t;i!=s;i=preV[i]){
edge &e=E[preV[i]][preE[i]];
e.cap-=d;
E[i][e.rev].cap+=d;
}
}
return make_pair(flow,cost);
}
}G;
int main() {
int t,k,n;
scanf("%d", &t);
while (t--) {
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
G.init(2*n+2);
int S = 0, T = 2 * n + 2;
G.add(S, n * 2 + 1, k, 0);
for (int i = 1; i <= n; i++) {
G.add(n * 2 + 1, i, 1, 0);
G.add(i, n + i, 1, -a[i]);
G.add(n + i, T, 1, 0);
}
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
if (a[i] <= a[j]) {
G.add(n + i, j, 1, 0);
}
}
}
PI ans=G.dijkstra(S,T,inf);
printf("%d
",-ans.second);
}
}

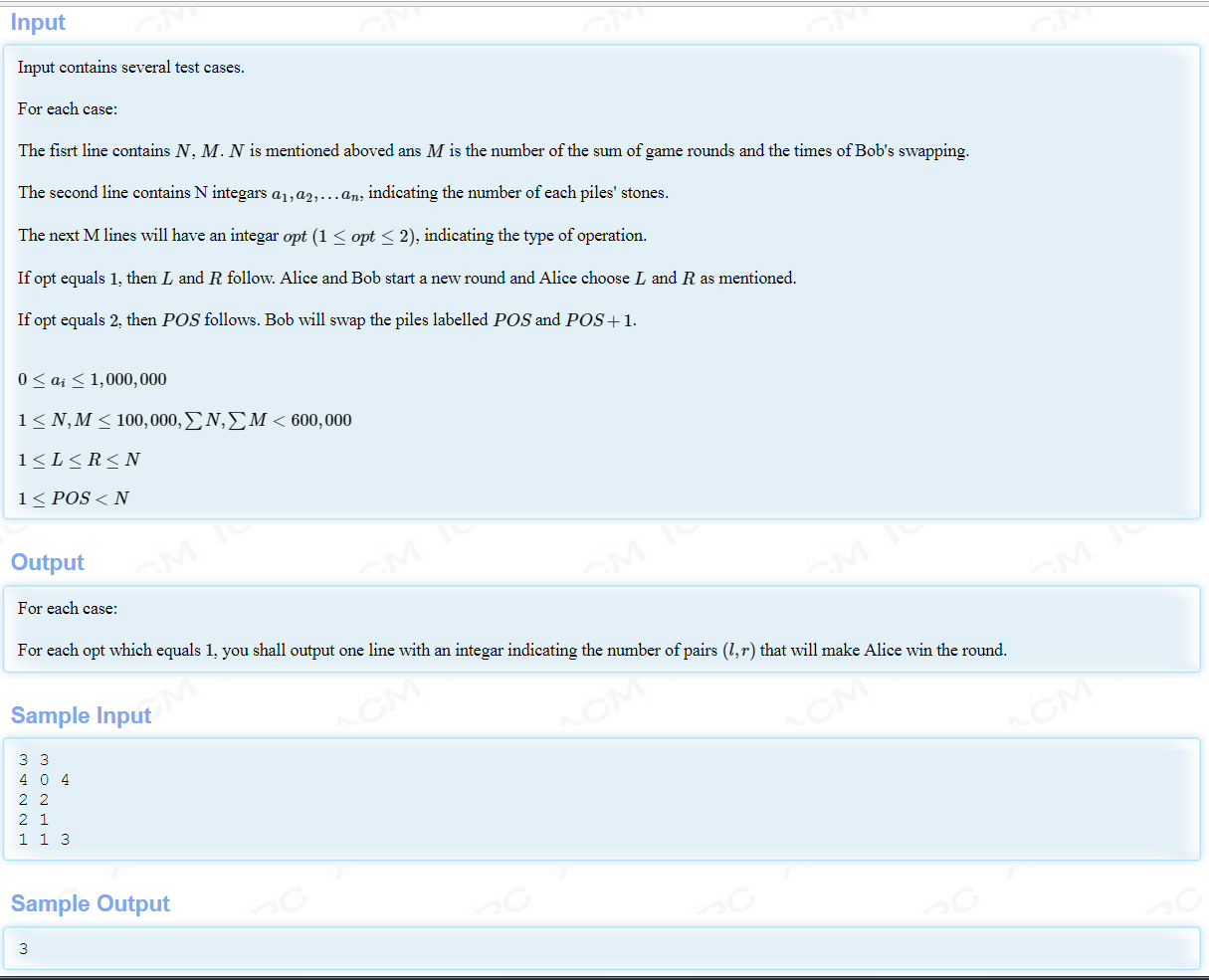
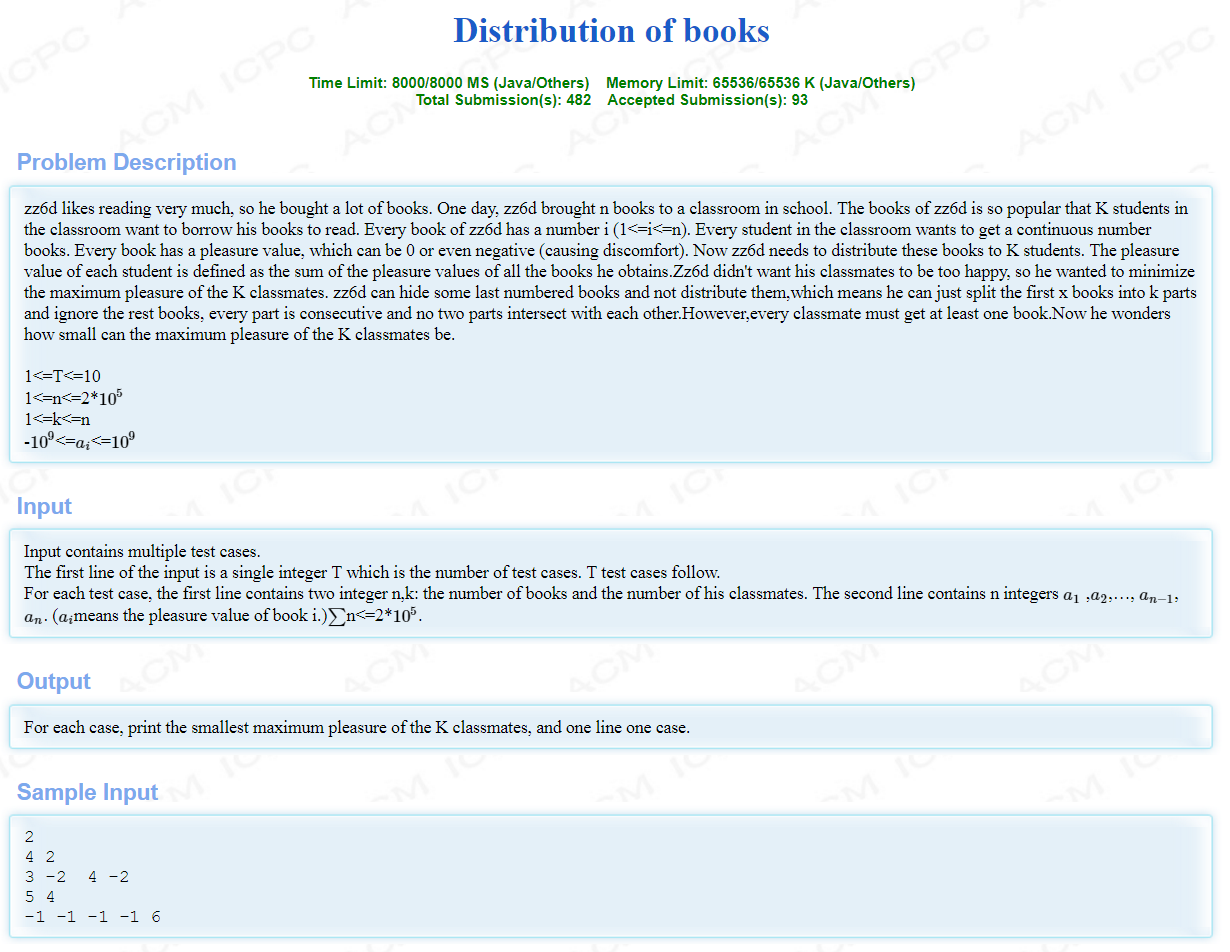

题意:要求把一个序列分成连续的k块(可以去掉后缀),使得权值和最大的那一块权值最小,求出这个最小值
思路:先求前缀和leftSum[],然后对前缀和离散化;
对leftSum[]排序并去重得到pre[];
设f[i]=前i个数最多能分成的块数;
二分答案,设答案为x;
则转移方程为f[i]=max(f[j])+1,leftSum[i]-leftSum[j]<=x,j<i
不能O(n^2)转移,想办法加速;
以离散化后的pre[]的rank为下标,f为权值建立线段树;
线段树需要实现单点修改、区间求最大值操作;
每次求f[i]时,令L=lower_bound(pre+1,pre+1+num,leftSum[i]-x),其中num为pre[]离散化后数字个数,
然后只需求得线段树[L,num]区间内的最大值_max,将f[i]更新为=_max+1即可,此时别忘了用新得到的f[i]去update线段树。
代码中注意一些小细节要处理好。
总时间复杂度为O(n*(logn)^2).
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e5+10;
int tot;
ll mx[maxn*4],b[maxn],dp[maxn],n,m,sum[maxn],a[maxn];
void build(int rt,int l,int r) {
if (l == r) {
mx[rt] = -1;
return;
}
int mid=(l+r)>>1;
build(rt << 1, l, mid);
build(rt << 1 | 1, mid + 1, r);
mx[rt] = max(mx[rt << 1], mx[rt << 1 | 1]);
}
void update(int rt,int l,int r,int p,ll val) {
if (l == r) {
mx[rt] = max(mx[rt], val);
return;
}
int mid = (l + r) >> 1;
if (p <= mid) update(rt << 1, l, mid, p, val); else update(rt << 1 | 1, mid + 1, r, p, val);
mx[rt] = max(mx[rt << 1], mx[rt << 1 | 1]);
}
int query(int rt,int l,int r,int L,int R) {
if (L > R) return -1;
if (L <= l && r <= R) {
return mx[rt];
}
int mid = (l + r) >> 1, ans = -1;
if (L <= mid) ans = max(ans, query(rt << 1, l, mid, L, R));
if (R > mid) ans = max(ans, query(rt << 1 | 1, mid + 1, r, L, R));
return ans;
}
bool solve(ll mid) {
build(1, 1, tot);
update(1, 1, tot, lower_bound(b + 1, b + 1 + tot, 0) - b, 0);
for (int i = 1; i <= n; i++) {
int p = lower_bound(b + 1, b + 1 + tot, sum[i] - mid) - b;
int p1 = lower_bound(b + 1, b + 1 + tot, sum[i]) - b;
int tmp = query(1, 1, tot, p, tot);
if (tmp == -1) dp[i] = -1;
else dp[i] = tmp + 1;
update(1, 1, tot, p1, dp[i]);
if (dp[i] >= m) return 0;
}
return 1;
}
int main() {
int _;
scanf("%d", &_);
while (_--) {
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%lld", &a[i]);
sum[i] = sum[i - 1] + a[i];
b[i] = sum[i];
}
b[n + 1] = 0;
sort(b + 1, b + 1 + n + 1);
tot = unique(b + 1, b + n + 1 + 1) - (b + 1);
ll l = -2e14, r = 2e14;
while (l < r) {
ll mid = (l + r) >> 1;
if (solve(mid)) l = mid + 1; else r = mid;
}
printf("%lld
", l);
}
}