莫比乌斯函数

莫比乌斯函数：

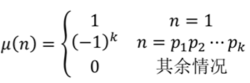
性质：

1.

2.

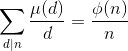
3.

若a,b互质，那么

[HAOI2011]Problem b

 

 

#include <bits/stdc++.h>

using namespace std;
const int N=20000;
bool vis[N+10];
int tot,prime[N+10],sum[N+10],mu[N+10];

void Mu(int n)
{
    mu[1]=1;
    for (int i=2; i<=n; i++)
    {
        if (!vis[i])
        {
            prime[++tot]=i;
            mu[i]=-1;
        }
        for (int j=1; j<=tot&&prime[j]*i<=n; j++)
        {
            vis[prime[j]*i]=1;
            if (i%prime[j]==0)
            {
                mu[i*prime[j]]=0;
                break;
            }
            mu[prime[j]*i]=-mu[i];
        }
    }
    for (int i=1; i<=n; i++)
    {
        sum[i]=sum[i-1]+mu[i];
    }
}
int ans(int n,int m)
{
    if (n>m)
    {
        swap(n,m);
    }
    int last,ret=0;
    for (int i=1; i<=n; i=last+1)
    {
        last=min(n/(n/i),m/(m/i));
        ret+=(n/i)*(m/i)*(sum[last]-sum[i-1]);
    }
    return ret;
}

int main()
{
    Mu(N);
    int _,a,b,c,d,k,ca=0;
    scanf("%d",&_);
    while (_--)
    {
        scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
        if (k==0)
        {
            printf("Case %d: 0
",++ca);
            continue;
        }
        a--;
        c--;
        a/=k;
        b/=k;
        c/=k;
        d/=k;
        int Ans=ans(b,d)-ans(a,d)-ans(b,c)+ans(a,c);
        printf("%d
",Ans);
    }
}

GCD

#include <bits/stdc++.h>

using namespace std;
const int N=200000;
typedef long long ll;
bool vis[N+10];
ll tot,prime[N+10],sum[N+10],mu[N+10];

void Mu(ll n)
{
    mu[1]=1;
    for (ll i=2; i<=n; i++)
    {
        if (!vis[i])
        {
            prime[++tot]=i;
            mu[i]=-1;
        }
        for (ll j=1; j<=tot&&prime[j]*i<=n; j++)
        {
            vis[prime[j]*i]=1;
            if (i%prime[j]==0)
            {
                mu[i*prime[j]]=0;
                break;
            }
            mu[prime[j]*i]=-mu[i];
        }
    }
    for (ll i=1; i<=n; i++)
    {
        sum[i]=sum[i-1]+mu[i];
    }
}
ll ans(ll n,ll m)
{
    if (n>m)
    {
        swap(n,m);
    }
    ll last,ret=0;
    for (ll i=1; i<=n; i=last+1)
    {
        last=min(n/(n/i),m/(m/i));
        ret+=(n/i)*(m/i)*(sum[last]-sum[i-1]);
    }
    return ret;
}

int main()
{
    Mu(N);
    int _,a,b,c,d,k,ca=0;
    scanf("%d",&_);
    while (_--)
    {
        scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
        if (k==0)
        {
            printf("Case %d: 0
",++ca);
            continue;
        }
        printf("Case %d: ",++ca);
        ll ans1=0,ans2=0;
        b/=k;
        d/=k;
        for (int i=1; i<=min(b,d); i++)
        {
            ans1+=mu[i]*(b/i)*(d/i);
        }
        for (int i=1; i<=min(b,d); i++)
        {
            ans2+=mu[i]*(min(b,d)/i)*(min(b,d)/i);
        }
        printf("%lld
",ans1-ans2/2);
    }
}

YY的GCD

// luogu-judger-enable-o2
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int N=10000001;
bool vis[N+10];
ll tot,f[N+10];
int prime[N+10],mu[N+10];
inline ll read()
{
    ll res=0,f=1;
    char ch=getchar();
    while (!isdigit(ch))
    {
        if (ch=='-')
        {
            f=-f;
        }
        ch=getchar();
    }
    while (isdigit(ch))
    {
        res=(res<<3)+(res<<1)+ch-'0';
        ch=getchar();
    }
    return f*res;
}
void Mu(ll n)
{
    mu[1]=1;
    for (register ll i=2; i<=n; i++)
    {
        if (!vis[i])
        {
            prime[++tot]=i;
            mu[i]=-1;
        }
        for (register ll j=1; j<=tot&&prime[j]*i<=n; j++)
        {
            vis[prime[j]*i]=1;
            if (i%prime[j]==0)
            {
                mu[i*prime[j]]=0;
                break;
            }
            mu[prime[j]*i]=-mu[i];
        }
    }
    for (register ll i=1;i<=tot;i++){
        for (ll j=1;j*prime[i]<=n;j++){
            f[j*prime[i]]+=mu[j];
        }
    }
    for (register ll i=1;i<=n;i++){
        f[i]=f[i-1]+f[i];
    }
}
void print(ll x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) print(x/10);
    putchar(x%10+'0');
}

int main(){
    ll _,m,n;
    Mu(N);
    _=read();
    while (_--){
        n=read();
        m=read();
        if (n>m){
            swap(n,m);
        }
        ll ans=0,r;
        for (register ll i=1;i<=n;i=r+1){
            r=min(n/(n/i),m/(m/i));
            ans+=(f[r]-f[i-1])*(n/i)*(m/i);
        }
        print(ans);
        putchar('
');
    }
    return 0;
}

[POI2007]ZAP-Queries

#include <bits/stdc++.h>

using namespace std;
const int N=200000;
typedef long long ll;
bool vis[N+10];
ll tot,prime[N+10],sum[N+10],mu[N+10];

void Mu(ll n)
{
    mu[1]=1;
    for (ll i=2; i<=n; i++)
    {
        if (!vis[i])
        {
            prime[++tot]=i;
            mu[i]=-1;
        }
        for (ll j=1; j<=tot&&prime[j]*i<=n; j++)
        {
            vis[prime[j]*i]=1;
            if (i%prime[j]==0)
            {
                mu[i*prime[j]]=0;
                break;
            }
            mu[prime[j]*i]=-mu[i];
        }
    }
    for (ll i=1; i<=n; i++)
    {
        sum[i]=sum[i-1]+mu[i];
    }
}
int main()
{
    Mu(N);
    int _,ca=0;
    ll b,d,k;
    scanf("%d",&_);
    while (_--)
    {
        scanf("%lld%lld%lld",&b,&d,&k);
        ll ans1=0,ans2=0;
        b/=k;
        d/=k;
        if (b>d){
            swap(b,d);
        }
        ans1=0;
        int r;
        for (int i=1; i<=b;i=r+1)
        {
            r=min(b/(b/i),d/(d/i));
            ans1+=(b/i)*(d/i)*(sum[r]-sum[i-1]);
        }
        printf("%lld
",ans1);
    }
}